2006年毕业生中考模拟考试(数学试卷)
一、细心填一填(本大题共有10小题,共30分.请把结果直接填在题中的横线上.只要你理解概念,仔细运算,相信你一定会填对的!)
1、(1)-3的相反数是 , ![]() 的算术平方根是
;
的算术平方根是
;
2、2006年世界杯足球赛6月份即将在德国开幕,预计观看本届世界杯的人数超过300亿人次,这个数据用科学记数法可表示为______ _____人。
3、设x1、x2是方程![]() 的两个实数根,则x1+x2=_____;x1·x2=_____.
的两个实数根,则x1+x2=_____;x1·x2=_____.
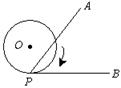
4、正比例函数y=kx的图象经过点(2,-1),则k的值为 。
![]() 5、初三(2)班40名学生献爱心捐款,情况如下表:
5、初三(2)班40名学生献爱心捐款,情况如下表:
捐款的中位数是_______,平均数是_________.
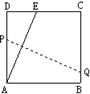
6、如图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为__________。
7、某商店出售下列形状的地板砖:①正三角形;②正方形;③正五边形;④正六边形.如果只限于用一种地板砖镶嵌地面,那么不能选购的地板砖序号是________。
8、已知⊙O1和⊙O2的半径分别为5和2,O1O2=3,则⊙O1和⊙O2的位置关系是________。
9、如图所示,![]() ,半径为
,半径为![]() 的⊙O切
的⊙O切![]() 于
于![]() 点.若将⊙O在
点.若将⊙O在![]() 上向右滚动,则当滚动到⊙O与
上向右滚动,则当滚动到⊙O与![]() 也相切时,圆心O移动的水平距离是 。
也相切时,圆心O移动的水平距离是 。
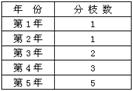
10、小明的爸爸在小明出生那年种了一棵树,这种树木的分枝生长规律如图所示,则预计当小明10岁时,即到第10年时,树木的分枝数为 。
|

二、精心选一选(本大题共6小题,每小题3分,共18分. 在每小题所给出的四个选项中,只有一项是正确的.把所选项前的字母代号填在题后的括号内. 只要你掌握概念,认真思考,相信你一定会选对!)
11、下列计算中.正确的有( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、已知在Rt△ABC中,∠C =90°,sinA=![]() ,则cosB的值等于( ).
,则cosB的值等于( ).
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
13、右图是护士统计一位病人的体温变化图,这位病人中午12时的体温约为 ( )
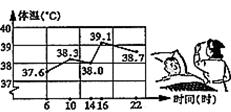 A、39.0℃ B、38.5℃
A、39.0℃ B、38.5℃
C、38.2℃ D、37.8℃
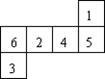
 14、如图是可以沿线折叠成一个带数字的立方体,每三个带数字的面交于立方体的一个顶点,则相交于一个顶点的三个面上的数字之和最小是 ( )
14、如图是可以沿线折叠成一个带数字的立方体,每三个带数字的面交于立方体的一个顶点,则相交于一个顶点的三个面上的数字之和最小是 ( )
A、 7 B、 8 C、9 D、 10
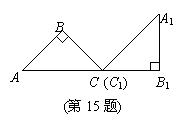
 15.如图,等腰Rt△ABC绕C点按顺时针旋转到△A1B1C1的位置(A,C,B1在同一直线上),∠B=90º,如果AB=1,那么AC运动到A1C1所经过的图形面积是(
)
15.如图,等腰Rt△ABC绕C点按顺时针旋转到△A1B1C1的位置(A,C,B1在同一直线上),∠B=90º,如果AB=1,那么AC运动到A1C1所经过的图形面积是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
16.如图所示,一块直角三角板ABC(∠A=30º)的斜
边AB与一个以r为半径的圆轮子相靠,若BD=1,
则r等于( )
(A)2 (B)![]() (C)1.5 (D)
(C)1.5 (D)![]()
三、认真答一答(本大题共3小题,满分20分. 解答需写出必要的文字说明、演算步骤或证明过程. 只要你积极思考, 细心运算, 你一定会解答正确的!)
17、⑴计算:![]() ; ⑵解不等式组
; ⑵解不等式组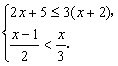
并写出不等式组的整数解.
18、(本小题满分7分)
如图,B、C是⊙O上的点,线段AB经过圆心O连结AC、BC,过点C作CD⊥AB于D,
∠ACD=2∠B.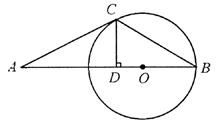 AC是⊙O的切线吗?为什么?
AC是⊙O的切线吗?为什么?
19、(本小题满分8分)
|
|
四.(8×2)
20、(本小题满分8分)
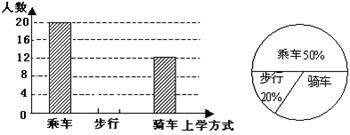
如图是某班学生上学方式的频数分布直方图和扇形统计图。
⑴求该班有多少名学生?
⑵补上频数分布直方图中“步行”的部分;
⑶在扇形统计图中,求“骑车”部分所占的圆心角度数。
⑷若全年级有500人,请你估计该年级步行人数。
21.(本题8分)
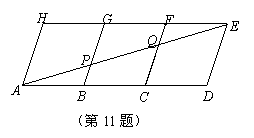 如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,
如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,
(1) 若AB=6,求线段BP的长;
(2) 观察图形,是否有三角形与△ACQ全等?并证明你的结论.
五,(8×1+9×1)
22.某城市为开发旅游景点,需要对古运河重新设计,加以改造,现需要A、B两种花砖共50万块,全部由某砖瓦厂完成此项任务.该厂现有甲种原料180万千克,乙种原料145万千克,已知生产1万块A砖,用甲种原料4.5万千克,乙种原料1.5万千克,造价1.2万元;生产1万块B砖,用甲种原料2万千克,乙种原料5万千克,造价1.8万元.
(1)利用现有原料,该厂能否按要求完成任务?若能,按A、B两种花砖的生产块数,有哪几种生产方案?请你设计出来(以万块为单位且取整数);
(2)试分析你设计的哪种生产方案总造价最低?最低造价是多少?
23、某医药研究所进行某一治疗病毒新药的开发,经过大量的服用试验后知:成年人按规定的剂量服用后,每毫克血液中含药量y微克(1微克=10-3毫克)随时间x小时的变化规律与某一个二次函数y=ax2+bx+c (a≠0)相吻合,并测得服用时(即时间为0时)每毫升血液中含药量为0微克;服用后2小时每毫升血液中含药量为6微克,服用后3小时,每毫升血液中含药量为7.5微克。
(1)求出含药量y(微克)与服药时间x(小时)的函数关系式;并画出0≤x≤8内的函数的图象的示意图;
(2)求服药后几小时才能使每毫升血液中含药量最大?并求出血液中的最大含药量;
(3)结合图象说明一次服药后的有效时间是多少小时?(有效时间为血液中含药量不为0的总时间)
六.(9×1+10×1)
24、(本小题满分9分)
已知:在矩形ABCD中,AB=6cm,AD=9cm,点P从点B出发,沿射线BC方向以每秒2cm的速度移动,同时,点Q从点D出发,沿线段DA以每秒1cm的速度向点A方向移动(当点Q到达点A时,点P与点Q同时停止移动),PQ交BD于点E.假设点P移动的时间为x(秒),△BPE的面积为y(cm2).
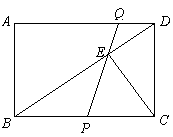 (1)求证:在点P、Q的移动过程中,线段BE的长度保持不变;
(1)求证:在点P、Q的移动过程中,线段BE的长度保持不变;
(2)求y关于x的函数解析式,并写出自变量的取值范围;
(3)如果CE=CP,求x的值.
25.(本题10分)
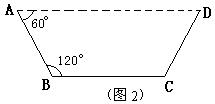
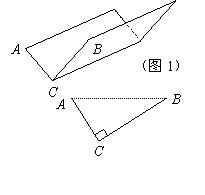
现有边长为120 cm的正方形铁皮,准备将它设计并制成一个开口的水槽,使水槽能通过的水的流量最大.
(1)小明认为,在水流速度一定的情况下,水槽的横截面面积越大,则通过水槽的水的流量越大.于是他对水槽的横截面设计了如下两种方案:
方案①:把它折成横截面为直角三角形的水槽(如图1).
若∠ACB=90°,设AC=x (cm),该水槽的横截面面积为y (cm2),请你写出y关于x的函数关系式(不必写出x的取值范围),并求出当x取何值时,y的值最大,最大值是多少?
方案②:把它折成横截面为等腰梯形的水槽(如图2).
若∠ABC=120°,请你求出该水槽的横截面面积的最大值,并与方案①中的y的最大值比较大小.
(2)请你再提供两种方案,使你所设计的水槽的横截面面积比小明设计的更大.画出你设计的草图,标上必要的数据(不要求写出解答过程).
 |