2006年中考全真模拟试卷（六）

（满分150分　 时间120分钟）

一、选择题（每题3分，共36分.每小题有四个选项，其中只有一个选项是正确的，将正确选项的字母填入下表相应的题号下面.）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

1、下列运算正确的是（　　　 ）

A、　　　　  B、

C、　　  　　D、

2、实验表明，人体内某种细胞的形状可近似地看作球，它的直径约为 0.m，则这个数用科学记数法表示是（　　　　　　）

（A）m　（B）m　　（C）m　　　（D）m

3、两圆的半径分别为3㎝和4㎝，圆心距为1㎝，则两圆的位置关系是(　　　)

（A）外切　　　　（B）内切　　　　（C）相交　　　　 （D）外离

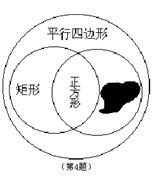
4、在学习“四边形”一章时，小明的书上有一图因不小心被滴上墨水（如图），看不清所印的字，请问被墨迹遮盖了的文字应是（　　  ）

A．等边三角形 　　  B．四边形　　　C．等腰梯形　 　　　D．菱形

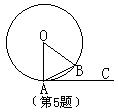
5、．如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=65º，则∠BAC=（　　 ）

A、35º　　　　B 、25º　　　　　 C、50º　　　　 D、65º

　　  　　 

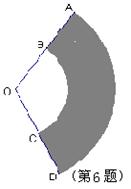
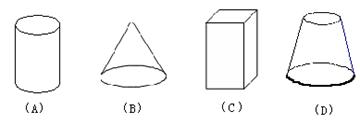
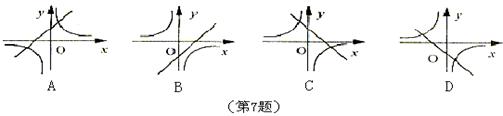
6、如图，将图中的阴影部分剪下来，围成一个几何体的侧面，使AB、DC重合，则所围成的几何体图形是（　　）

8、 已知(　　　　)

　 A、　　 B、　　  C、　　 D、

9、 如图是一束平行的光线从教室窗户射入教室的平面示意图，测得光线与地面所成的角，窗户的高在教室地面上的影长MN=米，窗户的下檐到教室地面的距离B C =1米（点M、N、C在同一直线上），则窗户的高AB为（　　 ）

A. 米　　 B. 米　　　　C. 2米　 　 D. 1.5米

10、在直角坐标系中，O为坐标原点，已知A（1，1），在x轴上确定点P，使AOP为等腰三角形，则符合条件的点P的个数共有（　　　　 ）

　　 A、4个　　　B、3个　　　 C、2个　　　 D、1个

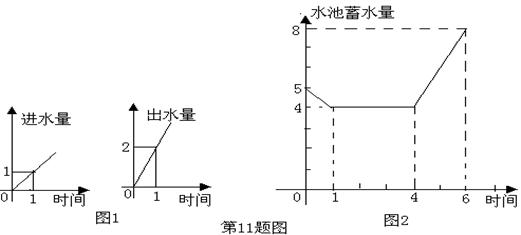
11、为了增强抗旱能力，保证今年夏粮丰收，某村新建了一个蓄水池，这个蓄水池安装了两个进水管和一个出水管（两个进水管的进水速度相同），一个进水管和一个出水管的进出水速度如图1所示。某天0点到6点（至少打开一个水管），该蓄水池的蓄水量如图2所示 ，并给出以下3个论断：①0点到1点不进水，只出水； ②1点到4点不进水，不出水；③4点到6点只进水，不出水，则一定正确的论断是（　　　　 ）

　　A、① ③　　　B、② ③　　　 C、③　　　　 D、① ② ③

 

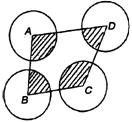12、如图，⊙A、⊙B、⊙C、⊙D相互外离，它们的半径都是1，顺次连结四个圆心得到四边形ABCD，则图形中四个扇形（阴影部分）的面积之和是（　　）
（A）2л　　　　 （B）л　

（C）л　　　　（D）

二、填空题 (每小题4分，共24分，请把答案填在其中的横线上.)

13．在等式的两个方格内分别填入一个数，使这两个数是互为相反数且等式成立。则第一个方格内的数是___________

14、 当m=_______时，分式的值为零。

15、 如图 ，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积是_____　___。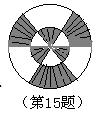

16、 如果－4是关于一元二次方程的一个根，则k的值为 　　　　  。

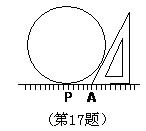
17、为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若测得PA=5cm，则铁环的半径是　　　　　  　　cm

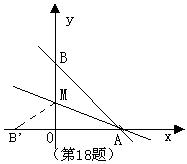
18、 直线与x轴、y轴分别交于点A和点B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点的B’处，则直线AM的解析式为 　　　　　　　　  。

三、解答题

19、化简：（本小题满分8分）

.

20、 （本题满分10分）

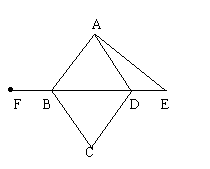
已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF。请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。

　　（1）连结_______　　 _____；（2）猜想：__　 ____=___　　___；

　　（3）证明：

 

21、（本题满分10分）

如图，小明、小华用4张扑克牌（方块2、黑桃4、黑桃5、梅花5）玩游戏，他俩将扑克牌洗匀后，背面朝上放置在桌面上，小明先抽，小华后抽，抽出的牌不放回。

（1）若小明恰好抽到了黑桃4。

①请在下边框中绘制这种情况的树状图；②求小华抽出的牌面数字比4大的概率。

（2）小明、小华约定：若小明抽到的牌面数字比小华的大，则小明胜；反之，则小明负。你认为这个游戏是否公平？说明你的理由。

22、（本题满分12分）

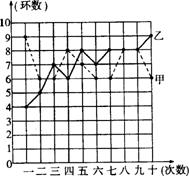射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示：　　

(1)根据右图所提供的信息填写下表：

	平均数	众数	方差
甲	7		1.2
乙			2.2

(2)如果你是教练，会选择哪位运动员参加比赛?请说明理由．

 

23、（本题满分12分）

在数学活动中，小明为了求的值（结果用n表示），设计如图7－1所示的几何图形。

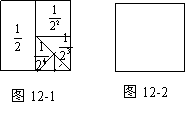（1）请你利用这个几何图形求

的值为__________。

（2）请你利用图7－2，再设计两个能求

的值的几何图形。

24、（本小题满分12分）

今年6月份，我市某果农收获荔枝30吨，香蕉13吨，现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳，已知甲种货车可装荔枝4吨和香蕉1吨，乙种货车可装荔枝香蕉各2吨；

(1)该果农按排甲、乙两种货车时有几种方案？请你帮助设计出来

(2)若甲种货车每辆要付运输费2000元，乙种货车每辆要付运输费1300元，则该果农应选择哪种方案？使运费最少？最少运费是多少元？

 

25、（本题满分12分）

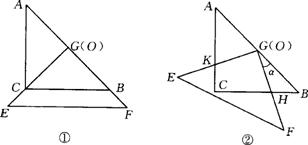
把两个全等的等腰直角三角形ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.

(1)在上述旋转过程中，BH与CH有怎样的数量关系？四边形BHGK的面积有何变化？证明你发现的结论；
(2)连接HK，在上述旋转过程中，设BH=，△GKH的面积为，求与之间的函数关系式，并写出自变量的取值范围；

(3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时的值；若不存在，说明理由.

26、（本题满分14分）

已知抛物线经过点A（，0）、B（m，0）（m>0），且与y轴交于点C．

⑴求a、b的值（用含m的式子表示）；

⑵如图所示，⊙M过A、B、C三点，求阴影部分扇形的面积S（用含m的式子表示）；

⑶在x轴上方，若抛物线上存在点P，使得以A、B、P为顶点的三角形与相似，求m的值．