
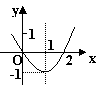 2006年中考数学第一轮复习专题训练
2006年中考数学第一轮复习专题训练
(八)
(二次函数及其应用)
一、填空题:(每题 3 分,共 36 分)
1、抛物线 y=-x2+1 的开口向____。
2、抛物线 y=2x2 的对称轴是____。
3、函数 y=2 (x-1)2 图象的顶点坐标为____。
4、将抛物线 y=2x2 向下平移 2 个单位,所得的抛物线的解析式为________。
5、函数 y=x2+bx+3 的图象经过点(-1, 0),则 b=____。
6、二次函数 y=(x-1)2+2,当 x=____时,y 有最小值。
7、函数 y=![]() (x-1)2+3,当 x____时,函数值 y 随 x 的增大而增大。
(x-1)2+3,当 x____时,函数值 y 随 x 的增大而增大。
8、将 y=x2-2x+3 化成 y=a (x-h)2+k 的形式,则 y=____。
9、若点 A ( 2, m) 在函数 y=x2-1 的图像上,则 A 点的坐标是____。
10、抛物线 y=2x2+3x-4 与 y 轴的交点坐标是____。
11、请写出一个二次函数以(2, 3)为顶点,且开口向上。____________。
12、已知二次函数 y=ax2+bx+c 的图像如图所示:则这个二次函数的解析式是 y=___。
二、选择题:(每题 4 分,共 24 分)
1、在圆的面积公式 S=πr2 中,s 与 r 的关系是( )
 A、一次函数关系 B、正比例函数关系 C、反比例函数关系 D、二次函数关系
A、一次函数关系 B、正比例函数关系 C、反比例函数关系 D、二次函数关系
2、已知函数 y=(m+2) x![]() 是二次函数,则 m 等于( )
是二次函数,则 m 等于( )
A、±2 B、2 C、-2 D、±![]()
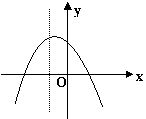
3、已知 y=ax2+bx+c 的图像如图所示,则 a、b、c 满足( )
A、a<0,b<0,c<0 B、a>0,b<0,c>0
C、a<0,b>0,c>0 D、a<0,b<0,c>0
4、苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足 S=![]() gt2(g=9.8),则 s 与 t 的函数图像大致是( )
gt2(g=9.8),则 s 与 t 的函数图像大致是( )
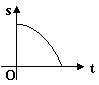
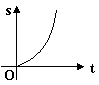
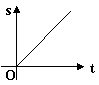
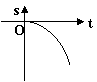
A B C D
5、抛物线 y=-x2 不具有的性质是( )
A、开口向下 B、对称轴是 y 轴 C、与 y 轴不相交 D、最高点是原点
6、抛物线 y=x2-4x+c 的顶点在 x 轴,则 c 的值是( )
A、0 B、4 C、-4 D、2
三、解答题:(每题 9 分,共 45 分)
1、如图,矩形的长是 4cm,宽是 3cm,如果将长和宽都增加 x cm,那么面积增加 ycm2,
① 求 y 与 x 之间的函数关系式。
② 求当边长增加多少时,面积增加 8cm2。

2、已知抛物线的顶点坐标是(-2,1),且过点(1,-2),求抛物线的解析式。
3、已知二次函数的图像经过(0,1),(2,1)和(3,4),求该二次函数的解析式。
4、用 6m 长的铝合金型材做一个形状如图所示的矩形窗框,应做成长、宽各为多少时,才能使做成的窗框的透光面积最大?最大透光面积是多少?

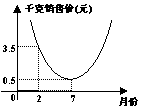
5、某农场种植一种蔬菜,销售员张平根据往年的销售情况,对今年种蔬菜的销售价格进行了预测,预测情况如图,图中的抛物线表示这种蔬菜销售价与月份之间的关系。
观察图像,你能得到关于这种蔬菜销售情况的哪些信息?(至少写出四条)
 |
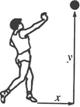
四、(10分)校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度 y (m) 与水平距离 x (m) 之间的函数关系式为 y=-![]() x2+
x2+![]() x+
x+![]() ,求小明这次试掷的成绩及铅球的出手时的高度。
,求小明这次试掷的成绩及铅球的出手时的高度。
 |
五、(10分)某企业投资100万元引进一条农产品生产线,预计投产后每年可创收33万元,设生产线投产后,从第一年到第 x 年维修、保养费累计为 y(万元),且 y=ax2+bx,若第一年的维修、保养费为 2 万元,第二年的为 4 万元。
求:y 的解析式。
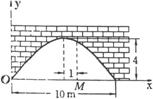
六、(12分)有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,如图所示,把它的图形放在直角坐标系中。
①求这条抛物线所对应的函数关系式。
②如图,在对称轴右边 1m 处,桥洞离水面的高是多少?
 |
七、(13分)商场销售一批衬衫,每天可售出 20 件,每件盈利 40 元,为了扩大销售,减少库存,决定采取适当的降价措施,经调查发现,如果一件衬衫每降价 1 元,每天可多售出 2 件。
① 设每件降价 x 元,每天盈利 y 元,列出 y 与 x 之间的函数关系式;
② 若商场每天要盈利 1200 元,每件应降价多少元?
③ 每件降价多少元时,商场每天的盈利达到最大?盈利最大是多少元?
答案 :
(八)
一、1、下 2、y 轴 3、(1, 0) 4、y=2x2-2 5、4 6、1 7、>1 8、(x-1)2+2
9、(2, 3) 10、(0, -4) 11、y=(x-2)2+3 12、(x-1)2-1
二、1、D 2、B 3、D 4、B 5、C 6、B
三、1、① y=(4+x) (3+x)-12 =7x+x2 ②8=7x+x2 x1=1,x2=-8
2、解:y=a (x+2)2+1 -2=a (1+2)2+1 a=-![]() ∴y=-
∴y=-![]() (x+2)2+1
(x+2)2+1
3、解:设 y=ax2+bx+c,则:![]() ,解得
,解得![]() ∴y=x2-2x+1
∴y=x2-2x+1![]()
4、解:设宽为 x、m,则长为 (3-![]() x)
m S=3x-
x)
m S=3x-![]() x2
=-
x2
=-![]() (x2-2x) =-
(x2-2x) =-![]() (x-1)2+
(x-1)2+![]()
当x=1时,透光面积最大为![]() m2。
m2。
5、①2月份每千克3.5元 ②7月份每千克0.5克 ③7月份的售价最低 ④2~7月份售价下跌
四、解:成绩10米,出手高度![]() 米
米
五、①解:![]() 解得
解得![]() ∴y=x2+x
∴y=x2+x
六、解:①设y=a (x-5)2+4 0=a (-5)2+4 a=-![]() ∴y=-
∴y=-![]() (x-5)2+4
(x-5)2+4
②当x=6时,y=-![]() +4=3.4(m)
+4=3.4(m)
七、解:①y=(40-x) (20+2x) =-2x2+60x+800 ②1200=-2x2+60x+800
x1=20,x2=10 ∵要扩大销售 ∴x取20元
③y=-2 (x2-30x)+800 =-2 (x-15)2+1250 ∴当每件降价15元时,盈利最大为1250元
