
 2006年中考数学第一轮复习专题训练
2006年中考数学第一轮复习专题训练
(二)
(代数式、整式及因式分解)
一、填空题:(每题 3 分,共 36 分)
1、对代数式 3a 可以解释为____________。
2、比 a 的 3 倍小 2 的数是____。
3、单项式-![]() 的系数是____,次数是____。
的系数是____,次数是____。
4、计算:(-3x![]() 2)3=________。
2)3=________。
5、因式分解:x2![]() -4
-4![]() =________。
=________。
6、去括号:3x3-(2x2-3x+1)=________。
7、把 2x3-x![]() +3x2-1 按 x 的升幂排列为________。
+3x2-1 按 x 的升幂排列为________。
8、一个多项式减去 4m3+m2+5,得 3m4-4m3-m2+m-8,则这个多项式为_____。
 9、若 4x2+kx+1 是完全平方式,则 k=____。
9、若 4x2+kx+1 是完全平方式,则 k=____。
10、已知 x2-ax-24 在整数范围内可分解因式,则整数 a 的值是____(填一个)。
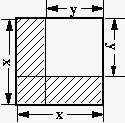
11、请你观察右图,依据图形的面积关系,使可得到一个非常熟悉的公式,这个公式为__________。
12、用边长为 1cm 的小正方形搭如下的塔状图形,则第 n 次所搭图形的周长是____cm。(用含 n 的代数式表示)
二、选择题:(每题 4 分,共 24 分)
1、用代数式表示“a 与 b 的差的平方”为( )
A、a-b2 B、a2-b2 C、(a-b)2 D、2a-2b
2、下列计算正确的是( )
A、2a3+a3=2a6 B、(-a)3·(-a2)=-a5
C、(-3a2)2=6a4 D、(-a)5÷(-a)3=a2
3、下列各组的两项不是同类项的是( )
A、2ax2 与 3x2 B、-1 和 3 C、2x![]() 2 和-
2 和-![]() 2x D、8x
2x D、8x![]() 和-8x
和-8x![]()
4、多项式 x2-5x-6 因式分解所得结果是( )
A、(x+6) (x-1) B、(x-6) (x+1) C、(x-2) (x+3) D、(x+2) (x-3)
5、若代数式 5x2+4x![]() -1 的值是 11,则
-1 的值是 11,则 ![]() x2+2x
x2+2x![]() +5 的值是( )
+5 的值是( )
A、11 B、![]() C、7 D、9
C、7 D、9
6、若(a+b)2=49,ab=6,则 a-b 的值为( )
A、-5 B、±5 C、5 D、±4
三、计算:(每题 6 分,共 24 分)
1、3x2-[7x-(4x-3)-2x2] 2、3a2b (2a2b2-3ab)
3、(2a-b) (-2a-b) 4、[(x+![]() )2-
)2-![]() (2x+
(2x+![]() )]÷2x
)]÷2x
四、因式分解:(每题 6 分,共 24 分)
1、-a+2a2-a3 2、x3-4x
3、a4-2a2b2+b4 4、(x+1)2+2(x+1)+1
五、(8分)下面的图形是旧边长为 l 的正方形按照某种规律排列而组成的。
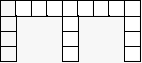 (1)观察图形,填写下表:
(1)观察图形,填写下表:
![]()
![]()
① ② ③
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 |
| 18 |
| 图形的周长 |
|
|
|
(2)推测第 n 个图形中,正方形的个数为____,周长为____。
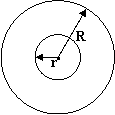 六、(8分)一个圆形花坛的中央修建了一个圆形喷水池,已知圆形花坛的半径 R=7.5m,圆形喷水池的半径 r=2.5m,求花坛中种有花草部分的面积。(π取3.1)
六、(8分)一个圆形花坛的中央修建了一个圆形喷水池,已知圆形花坛的半径 R=7.5m,圆形喷水池的半径 r=2.5m,求花坛中种有花草部分的面积。(π取3.1)
七、先化简,再求值。(每题 8 分,共 16 分)
1、已知:a=![]() ,求(2a+1)2-(2a+1) (2a-1) 的值。
,求(2a+1)2-(2a+1) (2a-1) 的值。
2、![]() a-2 (a-
a-2 (a-![]() b2)+(-
b2)+(-![]() a+
a+![]() b2),其中 a=3,b=-2。
b2),其中 a=3,b=-2。
八、(10分)已知一个多项式除以 2x2+x,商为 4x2-2x+1,余式为 2x,求这个多项式。
答案:(二)
一、1、每本练习本 a 元,三本共几元? 2、3a-2 3、-![]() 三次 4、-27x3y6
三次 4、-27x3y6
5、(x+2) (x-2) y 6、3x3-2x2+3x-1 7、-1-xy+3x2+2x3 8、3m4+m-3
9、±4 10、2 11、(x+y) (x-y)=x2-y2 12、4n
二、1、C 2、D 3、A 4、B 5、A 6、B
三、1、=3x2-[7x-4x+3-2x2] =3x2-[3x+3-2x2] =5x2-3x-3
2、=6a4b3-9a3b2 3、=b2-4a2 4、=[x2+2xy+y2-2xy-y2]÷2x =![]() x
x
四、1、=-(1-a)2 2、=x (x+2) (x-2) 3、=(a+b)2 (a-b)2 4、=(x+1+1)2=(x+2)2
五、(1)第一行:13 第二行:18,28,38 (2)5n+3 10n+8
六、πR2-πr2 =π(R+r) (R-r) =3.1×10×5 =155(m2)
七、1、解:(2a+1)·2 =4a+2 =![]() -1+2 =
-1+2 =![]() +1
+1
2、=![]() a-2a+
a-2a+![]() b2-
b2-![]() a+
a+![]() b2 =-3a+b2 =-3x3+(-2)2 =-9+4 =-5
b2 =-3a+b2 =-3x3+(-2)2 =-9+4 =-5
八、(2x2+x) (4x2-2x+1)+2x =8x4-4x3+2x2+4x3-2x2+x+2x =8x4+3x