2006年中考全真模拟试卷(二)
| 题号 | 一 | 二 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 总分 |
| 得分 |
一、选择题(每题3分,共36分.每小题有四个选项,其中只有一个选项是正确
的,将正确选项前的字母填入下表相应的题号下面.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、计算:-3+2的结果是
A、-5 B、-1 C、-6 D、6
2、纳米是一个长度单位,1纳米=10-9米,已知某种植物花粉的直径为35 000纳米,那么用科学记数法表示该花粉的直径为
(A)3.5×104米 (B)3.5×10-4米
(C)3.5×10-5米 (D)3.5×10-9米
3、下列二次根式,属于最简二次根式的是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、下列抽样调查:
①某环保网站就“是否支持使用可回收塑料购物袋”进行网上调查;
②某电脑生产商到当地一私立学校向学生调查学生电脑的定价接受程度;
③为检查过往车辆的超载情况,交警在公路上每隔十辆车检查一辆;
④为了解《中考指要》在学生复习用书中受欢迎的程度,随机抽取几个学校的初三年级中几个班级作调查.
其中选取样本的方法合适的有:
A、1个 B、2个 C、3个 D、4个
5、剪纸艺术是我国文化宝库中的优秀遗产,在民间广泛流传.我们扬州的民间剪纸作品享誉中外.下面的一组剪纸作品,属于中心对称图形的是 ( )
6、顺次连结等腰梯形各边中点所得的四边形一定是
A.菱形 B.矩形 C.梯形 D.正方形
7、如图,A、B、C是⊙O上的点,AB = 2㎝,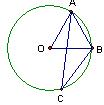 ∠ACB=30°,那么⊙O的半径为
∠ACB=30°,那么⊙O的半径为
A.![]() cm B.
cm B.
![]() cm
C. 2cm D.
4cm
cm
C. 2cm D.
4cm
8、如图,太阳光线与地面成60°角,一棵倾斜的大树与地面成30°角,这时测得大树在地面上影长约为10m,则大树得长约为(保留两个有效数字,下列数据供选用:![]()
![]()
A.13 B.15 C.17 D.19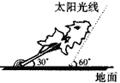

9、如图,□ABCD的周长为16cm,AC、BD相交于点O,
OE⊥AC交AD于E,则△DCE的周长为( )
A.4 cm B.6cm C.8cm D.10cm
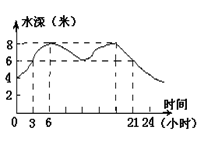 10、一港口受潮汐影响,某天24小时内港内水深变化大致如下图。港口规定:为了保证航行安全,只有当船底与水底间的距离不少于4米时,才能进出该港。一吃水深度(即船底低于水面的距离)为2米的轮船进出该港的时间最多为(单位:时)
10、一港口受潮汐影响,某天24小时内港内水深变化大致如下图。港口规定:为了保证航行安全,只有当船底与水底间的距离不少于4米时,才能进出该港。一吃水深度(即船底低于水面的距离)为2米的轮船进出该港的时间最多为(单位:时)
A.3 B.6 C.12 D.18
11、体育加试时,一女生扔实心球,实心球行进高度y(m)与水平距离 x(m)之间的关系是![]() ,已知女生实心球评分标准如下表:
,已知女生实心球评分标准如下表:
| 水平距离x(m) | 5.6 | 5.4 | 5.2 | 5.0 | 4.8 | 4.6 | 4.4 | |
| 分 值 | 15 | 14 | 13.5 | 13 | 12 | 11 | 10 |
 则该女生此项目的得分是:
则该女生此项目的得分是:
A、14分 B、13分 C、12分 D、11分
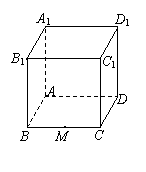
12、如图,正方体盒子的棱长为2,BC的中点为M,一只
蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距
离是
(A)![]() (B)
(B)![]() (C)5 (D)
(C)5 (D)![]()
二、填空题 (每题4分,共24分.)
13、函数y=![]() 中自变量x的取值范围是
。
中自变量x的取值范围是
。
14、如果多项式9x2-axy+4y2-b能用分组分解法分解因式,则符合条件的一组整数值是a= ,b= .
15、写出一个图象位于二、四象限的反比例函数表达式是_________________.
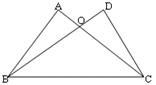 16、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是_____________________________(只需填写一个你认为适合的条件).
16、已知:如图,∠ACB=∠DBC,要使△ABC≌△DCB,只需增加的一个条件是_____________________________(只需填写一个你认为适合的条件).
17、已知在平面直角坐标系中,两圆的圆心分别是(![]() ,0)和(0,1),它们的半径长分别是3和5,
那么这两个圆的位置关系是 ____。
,0)和(0,1),它们的半径长分别是3和5,
那么这两个圆的位置关系是 ____。
(02长沙市)18、某城市自来水收费实行阶梯水价,收费标准如下表所示,用户5月份交水费45元,则所用水为 吨.
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
三、解答下列各题 (本大题共8题,计90分.解答时应写明演算步骤、证明过程或必要的文字说明.)
19、(本题满分8分)有这样的一道题:“计算:![]() 的值,其中x=2004。”甲同学把“x=2004”错抄成“x=2040”,但他的计算结果也是正确的。你说这是怎么回事?
的值,其中x=2004。”甲同学把“x=2004”错抄成“x=2040”,但他的计算结果也是正确的。你说这是怎么回事?
20、(本题满分10分)如图,在等腰梯形ABCD中,AB∥CD,AC、BD是对角线,将△ABD沿AB向下翻折到△ABE的位置,试判定四边形AEBC的形状,并证明你的结论.
21、(本题满分10分)某校初三(1)班、(2)班各有49名学生,两班在一次数学测验中的成绩统计如下表:
| 班 级 | 平均分 | 众数 | 中位数 | 标准差 |
| 初三(1)班 | 79 | 70 | 87 | 19.8 |
| 初三(2)班 | 79 | 70 | 79 | 5.2 |
(1)请你对下面的一段话给予简要分析:初三(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均79分,得70分的人最多,我得了85分,在班里可算上游了!”
(2)请你根据表中的数据,对这两个班的测验情况进行简要分析,并提出教学建议。
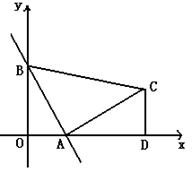
22、(本题满分12分) 已知如图,直线y=-2x+2与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D。
(1)求点A、B的坐标和AD的长。
(2)求过B、A、D三点的抛物线的解析式。
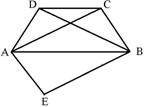
 23、(本题满分12分)某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
23、(本题满分12分)某电脑公司现有A,B,C三种型号的甲品牌电脑和D,E两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑.
(1) 写出所有选购方案(利用树状图或列表方法表示);
(2) 如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A型号电脑,求购买的A型号电脑有几台.
24、(本题满分12分)如图, 这些等腰三角形与正三角形的形状有差异,我们把它与正三角形的接近程度称为“正度”。在定义“正度”时,要求“正度”的值是非负数, 而且保证相似三角形的“正度”相等。
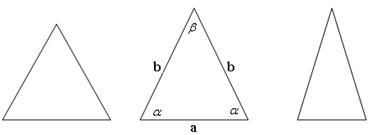
设等腰三角形的底和腰分别为a、b,底角和顶角分别为![]() 、
、![]() 。
。
同学甲认为:可用式子![]() 来表示“正度”,
来表示“正度”,![]() 的值越小,表示等腰三角形越接近正三角形;
的值越小,表示等腰三角形越接近正三角形;
同学乙认为:可用式子![]() 来表示“正度”,
来表示“正度”,![]() 的值越小,表示等腰三角形越接近正三角形。
的值越小,表示等腰三角形越接近正三角形。
探究:(1)他们的方案哪个较为合理,为什么?
(2)对你认为不够合理的方案,请加以改进(给出式子即可);
(3)请再给出一种衡量“正度”的方案。
 25、(本题满分12分)教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
25、(本题满分12分)教室里放有一台饮水机(如图),饮水机上有两个放水管.课间同学们依次到饮水机前用茶杯接水.假设接水过程中水不发生泼洒,每个同学所接的水量都是相等的.两个放水管同时打开时,他们的流量相同.放水时先打开一个水管,过一会儿,再打开第二个水管,放水过程中阀门一直开着.饮水机的存水量y(升)与放水时间x(分钟)的函数关系如图所示:
(1)求出饮水机的存水量y(升)与放水时间x(分钟)(x≥2)的函数关系式;
(2)如果打开第一个水管后,2分钟时恰好有4个同学接水结束,则前22个同学接水结束共需要几分钟?
(3)按(2)的放法,求出在课间10分钟内班级中最多有多少个同学能及时接完水?
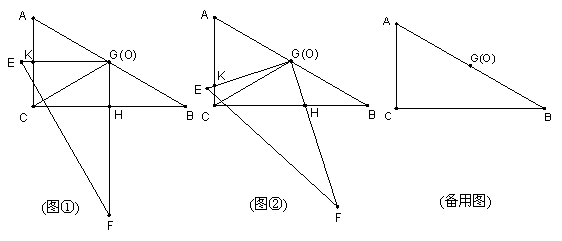
26、(本题满分14分)把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.
(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;
(3)在②下,连接HK,在上述旋转过程中,设GH=![]() ,△GKH的面积为
,△GKH的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(4)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.