数学摸底测验试卷
一.选择题(每小题4分,共40分)
1.计算2-3的结果是 ( )
 A.
-1 B. 0 C. 1 D. 2
A.
-1 B. 0 C. 1 D. 2
2.不等式2-x<1的解集是 ( )
A. x>1 B. x>-1 C. x<1 D. x<-1
3.如图是某地一天的气温随时间的图象,
根据图象可知,在这一天中最高气温与达
![]()
![]() 到最高气温的时刻分别是 ( )
到最高气温的时刻分别是 ( )
![]()
![]() A. 14℃, 12时 B. 4℃, 2时
A. 14℃, 12时 B. 4℃, 2时
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() C.12℃, 14时 C.
2℃, 4时
C.12℃, 14时 C.
2℃, 4时
4.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是( )
A ![]() B。
B。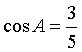
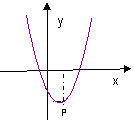 C
C
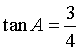 D.
D.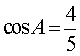
5.如图,抛物线的顶点P的坐标是(1,-3),
则此抛物线对应的二次函数是( )
A.最大值为1 B.最小值为-3
 C最大值为-3
D最小值为-3
C最大值为-3
D最小值为-3
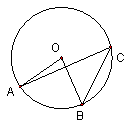
6.如图,A、B、C三点在⊙O上,且∠AOB=80°,
则∠ACB等于( )
A.100° B.80° C.50° D.40°
7以下四家银行行标中,轴对称图形的有 ( )

A B C D
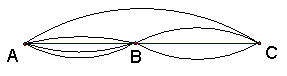 8.如图,从A地到C地,可供选择的方案是
8.如图,从A地到C地,可供选择的方案是
走水路、走陆路走空中。从A地到B地
有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地。则从A地到C可供选择的方案有 ( )
A.20种 B.8种 C.5种 D.13种
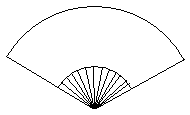 9.如图,一把单面绸扇完全打开后外侧两竹条AB
9.如图,一把单面绸扇完全打开后外侧两竹条AB
和CD的夹角为120°,AB的长为25cm,
绸布部分的寛BD为15cm,则这把扇子
绸布部分BDEC的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
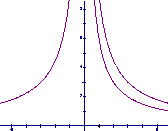 10.如图。三个反比例函数
10.如图。三个反比例函数![]() ,
,
在x轴上方的图象,由此观察得到![]()
的大小关系为( )
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
 二.填空题(每小题5分,共30分)
二.填空题(每小题5分,共30分)
11.因式分解:![]() _______
_______
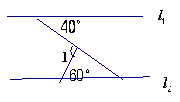
12如图,![]() ∥
∥![]() ,则∠1=___。
,则∠1=___。
 13.如图是一个正方体纸盒的展开图,
13.如图是一个正方体纸盒的展开图,
在其中的四个正方形内标有数字1,2,3
和-3。要在其余四个正方形内分别填上-1,-2,
使得按虚线折成正方体后,相对面上的两数互
 为相反数,则A处应填____。
为相反数,则A处应填____。
14.如图,AB是⊙O的直径,弦CD⊥AB,
E为垂足,若AB=9,BE=1,则CD=___。
 15.如图,将一副直角三角板叠在一起,使直角
15.如图,将一副直角三角板叠在一起,使直角
顶点重合于O点,则∠AOB+∠DOC=___°
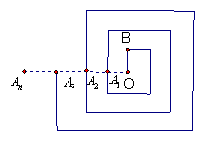 16.如图是一回形图,其回形通道的宽和OB
16.如图是一回形图,其回形通道的宽和OB
的长均为1,回形线与射线OA交于![]() ,
,
若从O点到回形线为第一圈(长为7),从![]() 点
点
到![]() 点的回形线为第二圈,……,依此类推。
点的回形线为第二圈,……,依此类推。
则第十圈的长为____。
三.解答题(共80分)
17.(1)计算:![]() (4分)
(4分)
(2)解方程: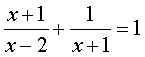 (4分)
(4分)
18.(8分)某公司员工的月工资如下:(单位:元)
| 员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E |
| 月工资 | 6000 | 3500 | 1500 | 1500 | 1500 | 1100 | 1000 |
(1)该公司员工月工资的中位数是____,众数是___。
(2)该公司员工月工资的平均数是多少?
(3)用平均数还是中位数和众数描述该公司员工月工资的一般水平比较恰当?
19.(8分)已知一次函数图象经过A(-2,-3)﹑B(1,3)两点。(1)求此函数的表达式;(2)试判断点P(-1,1)是否在这个一次函数的图象上?
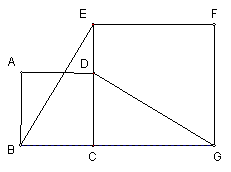 20.(8分)如图,正方形ABCD的边CD在正方形ECGF的边上,连接BE﹑DG。观察猜想BE与DG之间的大小关系,并说明你的结论。
20.(8分)如图,正方形ABCD的边CD在正方形ECGF的边上,连接BE﹑DG。观察猜想BE与DG之间的大小关系,并说明你的结论。
21(10分)随着我国人口增长速度的减慢,小学入学儿童数量每年按逐渐减少的趋势发展,某区2004年和2005年小学入学儿童人数之比为8︰7,且2004年入学人数的2倍比2005年入学人数的3倍少1500人,某人估计2006年入学儿童数将超过2300人,请你通过计算,判断他的估计是否符合当前的变化趋势。
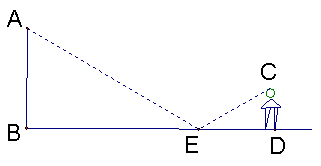
22(12分)如图,把一面镜子放在离某建筑物(AB)50m远的E处,然后沿着直线BE向后退到点D,这时恰好在镜子里看到物的顶点A。量得ED=3cm,观察者眼睛离地面1﹒5m。求建筑高度。
 |
23.(12分)阳光小区有一块正方形的空地,设计用作休闲场地。如图1是小聪根据正方形空地的设计方案示意图(阴影部分为绿化场地)。请你用圆规和直尺在同样的正方形内(图2、
图3),画出两种不同于小聪的设计方案示意图,使它们的绿化场地面积(用阴影表示)与已知图1的绿化场地面积相同(不要求写画法)。

24.(14分)如图,直角梯形ABCD中,AD∥BC,∠B=90°,
AD=24cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s
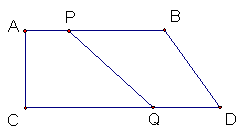 的速度运动,动点Q从C点开始沿CB边向B以2cm/s的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t(s),
的速度运动,动点Q从C点开始沿CB边向B以2cm/s的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t(s),
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)若AB=8,当t为何值时,P、Q的距离为10?