中考专题　阅读理解题

1（甘肃）（8分）阅读以下材料并填空．
平面上有n个点（n≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？
⑴ 分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线；……
⑵ 归纳：考察点的个数n和可连成直线的条数，发现：


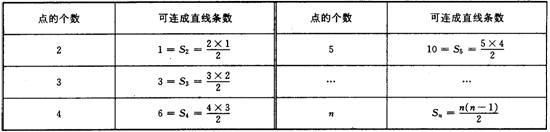
⑶ 推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n－l）种取法，所以一共可连成 n（n－1）条直线，但 AB与 BA是同一条直线，故应除以 2，即。
⑷ 结论：．

试探究以下问题：
平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
⑴ 分析：当仅有3个点时，可作　　　　　 个三角形；当有4个点时，可作　　　　  个三角形；当有5个点时，可作　　　　　 个三角形；……
⑵ 归纳：考察点的个数n和可作出的三角形的个数，发现：

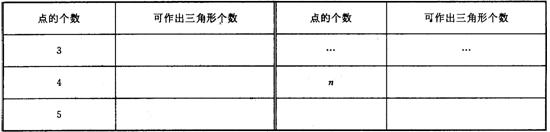
⑶ 推理：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　；
⑷ 结论：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  ；

2（广西）（本题满分11分）阅读下列材料：
十六大提出全面建设小康社会．国际上常用恩格尔系数（记作n）来衡量一个国家和地区人民生活水平的状况，它的计算公式为：


根据上述材料，解答下列问题：
某校初三学生对我市一个乡的农民家庭进行抽样调查．从1997年至2002年间，该乡每户家庭消费支出总额每年平均增加500元，其中食品消费支出总额每年平均增加200元．1997年该乡农民家庭平均刚达到温饱水平，已知该年每户家庭消费支出总额平均为8000元．
（1）1997年该乡平均每户家庭食品消费支出总额为多少元？
（2）设从1997年起m年后该乡平均每户的恩格尔系数为（m为正整数）．请用m的代数式表示该乡平均每户当年的恩格尔系数，并利用这个公式计算2003年该乡平均每户的恩格尔系数（百分号前保留整数）．
（3）按这样的发展，该乡将于哪年开始进人小康家庭生活？该乡农民能否实现十六大提出的2020年我国全面进人小康社会的目标？

3（茂名）王老师要求学生进行编题。解题训练，其中小聪同学编的练习题是：
设k＝3，方程的两个实数根是,，求的值．
小明同学对这道题的解答过程是：
解：∵ k＝3　　∴ 已知方程是，
　又∵ +=3，•=3，
∴ =
　即　=1。
（1）请你针对以上的练习题和解答的正误作出判断，再简述理由；（4分）
（2）请你只对小聪同学所编的练习题中的k另取一个适当的正整数，其他条件不变，改求的值（5分）
解：

4（青岛）在抗击“非典”的斗争中，某市根据疫情的发展状况，决定全市中、小学放假两周，以切实保障广大中、小学生的安全．腾飞中学初三（1）班的全体同学在自主完成学习任务的同时，不忘关心同学们的安危，两周内全班每两个同学都通过一次电话，互相勉励，共同提高．如果该班有56名同学，那么同学们之间共通了多少次电话？
为解决该问题，我们可把该班人数n与通电话次数s间的关系用下列模型来表示：

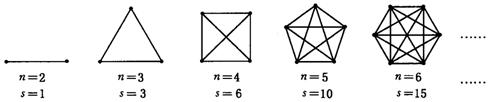
⑴ 若把n作为点的横坐标，s作为纵坐标，根据上述模型中的数据，在给出的平面直角坐标系中，描出相应各点，并用平滑的曲线连接起来；
⑵ 根据日中各点的排列规律，猜一猜上述各点会不会在某一函数的图像上？如果在，求出该函数的解析式；
⑶ 根据⑵中得出的函数关系式，求该班56名同学间共通了多少次电

话．

5（烟台）阅读下面材料，再回答问题：
一般地，如果函数y＝f（x）对于自变量取值范围内的任意x，都有f（－x）＝－f（x），那么y＝f（x）就叫做奇函数；如果函数y＝f（x）对于自变量取值范围内的任意x，都有f（－x）＝f（x），那么y＝f（x）就叫做偶函数．
例如：
当x取任意实数时，
即f（－x）＝－f（x）
所以为奇函数
又如f（x）＝
当x取任意实数时，
即f（－x）＝f（x）
所以f（x）＝是偶函数
问题（1）：下列函数中
①　　②　　③　 ④　　 ⑤
所有奇函数是　　　　　　　 ，所有偶函数是　　　　　　　　　　 （只填序号）．
问题（2）：请你再分别写出一个奇函数、一个偶函数．

6（随州）课本上有这样一题：已知，如图（1），O点在△ABC内部，连AO、BO、CO，A’、B’、C’分别在AO、BO、CO上，且AB∥A’B’、BC∥B’C’．
求证：△OAC∽△OA’C’．若将这题图中的O点移至△ABC外，如图（2），其它条件不变，题中要求证的结论成立吗？
（1）在图（2）基础上画出相应的图形，观察并回答：　　　　　　 （填成立或不成立）．
（2）证明你（1）中观察到的结论．

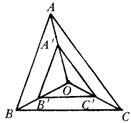
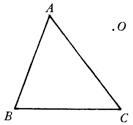
图1　 图2

7（新疆）已知：如图，AB是⊙O的直径，CD是弦，AE⊥CD，垂足是E，BF⊥CD，垂足是F，求证：CE＝DF．小明同学是这样证明的：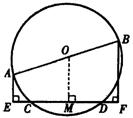
证明：∵  OM⊥CD　　　　　　　　　　　  订正：
　　　　　　　  ？
　　∴ CM＝MD
　　　　  ∵ AE∥OM∥BF
　　　　　　　  ？
∴ ME＝MF
　　　？
∴ ME－CM＝MF－MD
即　CE＝DF
横线及问号是老师给他的批注，老师还写了如下评语：“你的解题思路很清晰．但证明过程欠完整，相信你再思考一下，一定能写出完整的证明过程”．请你帮助小明订正此题，好吗？

8（淮安）已知关于x的一元二次方程x²-mx+2m-1=0的两个实数根的平方和为23，求m的值。

某同学的解答如下：

解：设x₁、x₂是方程的两根，

　　由根与系数的关系，得x₁+x₂= -m,　 x₁x₂=2m-1;

由题意，得x₁²+x₂²=23;

又x₁²+x₂²=(x₁+x₂)²-2x₁x₂;

∴m²-2(2m-1)=23.

解之，得m₁=7, m₂=-3,

所以,m的值为7或-3。

上述解答中有错误，请你指出错误之处，并重新给出完整的解答