2006年中考全真模拟试卷（八）
（满分150分，时间：120分钟）
一、选择题(每题3分，共36分.每小题有四个选项，其中只有一个选项是正确的，将正确选项的字母填入下表相应的题号下面.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
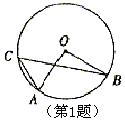
1、如图，圆周角
的度数为
，则圆心角
的度数为（
）
A. B.
C.
D.
2、如图可以看作是一个等腰直角三角形旋转若干次而生成的，则每次旋转的度数可以是（ ）
A．
B．
C．
D．
3、下列图形中，不可能围成正方体的有（ ）个
A. 1 B. 2 C. 3 D. 4
4.
4、把分式方程
的两边同时乘以(x-2), 约去分母，得
A．1-(1-x)=1 B．1+(1-x)=1 C．1-(1-x)=x-2 D．1+(1-x)=x-2
5、下列四个命题
(1)对角线互相垂直的平行四边形是正方形.
(2)对角线相等的梯形是等腰梯形.
(3)过弦的中点的直线必经过圆心.
(4)圆的切线垂直于经过切点的半径.
其中正确的命题是( )
A．(1)、(2) B．(2)、(3) C．(2)、(4) D.(1)、(4)
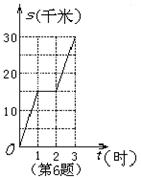
6、 如图是某人骑自行车的行驶路程
（千米）与行驶时间
（时）的函数图象，下列说法不正确的是（ ）
A、从0时到3时，行驶了30千米 B、从1时到2时匀速前进
C、从1时到2时在原地不动 D、从0时到1时与从2时到3时的行驶速度相同
7、图1 是甲、乙、丙三人玩跷跷板的示意图（支点在中点处），则甲的体重的取值范围在数轴上表示正确的是（ ）
8、 如图3是2004年3月份的日历表，任意圈出一竖列上相邻的三个数，请你运用方程思想来研究，发现这三个数的和不可能是（ ）
A．69 B．54 C．27 D．40
9、在一个暗箱里放入除颜色以外其他都相同的3个红球和11个黄球，搅拌均匀后随机任取一个球，取到是红球的概率是（ ）
A、
B、
C、
D、
10、已知Rt△ABC的斜边AB=5，一条直角边AC=3，以直线BC为轴旋转一周得到一个圆锥，则这个圆锥的侧面积为（ ）
A、8π B、12π C、15π D、20π
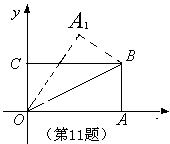
11、如图，在直角坐标系中，将矩形
沿
对折，使点
落在点
处，已知
,
，则点的坐标是（ ）．
A．（
，
） B．（，3） C．（，） D．（
，）
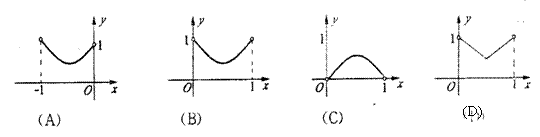
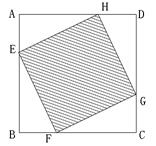12、 如图，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点， 且AE=BF=CG=DH, 设小正方形EFGH的面积为
，AE为
，则关于的函数图象大致是（ ）
二、填空题(每小题4分，共24分，请把答案填在其中的横线上.)
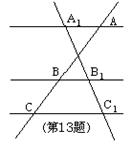
13、如图，直线A1A∥B1B∥C1C，若AB=8，BC=4，A1B1=6，则线段B1C1的长是 。
14、在数轴上，与表示－1的点距离为3的点所表示的数是 .
15、为了改善住房条件，小亮的父母考察了某小区的
两套楼房，套楼房在第
层楼，
套楼房在第
层楼，套楼房的面积比套楼房的面积大24平方米，两套楼房的房价相同，第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍．为了计算两套楼房的面积，小亮设套楼房的面积为
平方米，套楼房的面积为
平方米，根据以上信息可列出方程组为 。
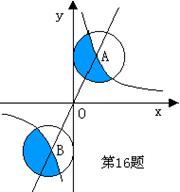
16、图中正比例函数和反比例函数的图像相交于A、B两点，分别以A、B两点为圆心，画与y轴相切的两个圆，若点A的坐标为（1，2），则图中两个阴影部分面积的和是 。
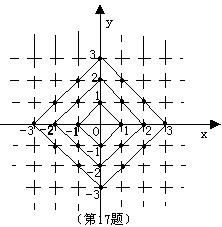
17、在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点。观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有 个。
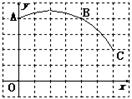18、如图，直角坐标系中一条圆弧经过网格点A、B、C，其中，B点坐标为
，则该圆弧所在圆的圆心坐标为__________。
三、解答题(本大题共8题，计90分.解答时应写明演算步骤、证明过程或必要的文字说明.)
19、（本题满分8分）
| 组别 | 分 组 | 频 数 | 频率 |
| 1 | 49.5～59.5 | 60 | 0.12 |
| 2 | 59.5～69.5 | 120 | 0.24 |
| 3 | 69.5～79.5 | 180 | 0.36 |
| 4 | 79.5～89.5 | 130 |
|
| 5 | 89.5～99.5 |
| 0.02 |
| 合 计 |
| 1.00 | |
为配和新课程的实施，某市举行了“应用与创新”知识竞赛，共有1万名学生参加了这次竞赛（满分100分，得分全为整数）。为了解本次竞赛成绩情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表：
解答下列问题：
（1）在这个问题中，总体是_________________
____________________，样本容量
＝ ；
（2）第四小组的频率c＝ ；
（3）被抽取的学生成绩的中位数落在第几小组内？
（4）若成绩在90分以上（含90分）的学生获一等奖，请你估计全市获一等奖的人数。
20、（本小题满分10分）
小明的家在某公寓楼AD内，他家的前面新建了一座大厦BC，小明想知道大厦的高度，但由于施工原因，无法测出公寓底部A与大厦底部C的直线距离，于是小明在他家的楼底A处测得大厦顶部B的仰角为
，爬上楼顶D处测得大厦的顶部B的仰角为
，已知公寓楼AD的高为60米，请你帮助小明计算出大厦的高度BC。
21、（本题满分10分）
甲、乙两同学开展“投球进筐”比赛，双方约定：① 比赛分6局进行，每局在指定区域内将球投向筐中，只要投进一次后该局便结束；② 若一次未进可再投第二次，以此类推，但每局最多只能投8次，若8次投球都未进，该局也结束；③ 计分规则如下：a. 得分为正数或0；b. 若8次都未投进，该局得分为0；c. 投球次数越多，得分越低；d. 6局比赛的总得分高者获胜 .
(1) 设某局比赛第n(n=1,2,3,4,5,6,7,8)次将球投进，请你按上述约定，用公式、表格或语言叙述等方式，为甲、乙两位同学制定一个把n换算为得分M的计分方案；
(2) 若两人6局比赛的投球情况如下(其中的数字表示该局比赛进球时的投球次数，“×”表示该局比赛8次投球都未进)：
| 第一局 | 第二局 | 第三局 | 第四局 | 第五局 | 第六局 | |
| 甲 | 5 | × | 4 | 8 | 1 | 3 |
| 乙 | 8 | 2 | 4 | 2 | 6 | × |
根据上述计分规则和你制定的计分方案，确定两人谁在这次比赛中获胜.
22、 (本题满分12分)
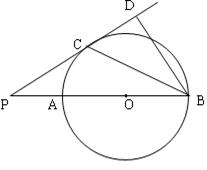已知：如图，AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC。
求证：（1）BC平分∠PBD；
（2）BC2=AB·BD。
23、（本题满分12分）
心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化。开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散。经过实验分析可知，学生的注意力指标数随时间（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
(1) 开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？
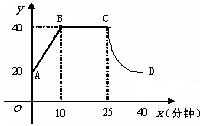（3）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？
24、(本题满分12分)
为了加强学生的交通安全意识，某中学和交警大队联合举行了“我当一日小交警”活动，星期天选派部分学生到交通路口值勤，协助交通警察维护交通秩序．若每一个路口安排4人，那么还剩下78人；若每个路口安排8人，那么最后一个路口不足8人，但不少于4人．求这个中学共选派值勤学生多少人？共有多少个交通路口安排值勤？
25、（本题满分12分）
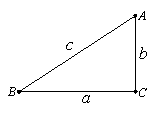
在△ABC中，∠A、∠B、∠C所对的边分别用a、b、c表示。
（Ⅰ）如图，在△ABC中，∠A＝2∠B，且∠A＝60°。
求证：a2＝b（b＋c）
 |
（Ⅱ）如果一个三角形的一个内角等于另一个内角的2 倍，我们称这样的三角形为“倍角三角形”。本题第一问中的三角形是一个特殊的倍角三角形，那么对于任意的倍角三角形ABC，其中∠A＝2∠B，关系式a2＝b（b＋c）是否仍然成了？并证明你的结论；
 |
（Ⅲ）试求出一个倍角三角形的三条边的长，使这三条边长恰为三个连续的正整数。
26、 （本题满分14分）
如图，在直角坐标系中，O是坐标原点，A、B、C三点的坐标分别为A（18，0），B（18，6），C（8，6），四边形OABC是梯形。点P、Q同时从原点出发，分别作匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC，CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动。
（1） 求出直线OC的解析式及经过O、A、C三点的抛物线的解析式；
（2） 试在（1）中的抛物线上找一点D，使得以O、A、D为顶点的三角形与三角形AOC全等，请直接写出点D的坐标。
（3） 设从出发起，运动了t秒，如果点Q的速度为每秒2个单位，试写出点Q的坐标，并写出此时t的取值范围。
（4） 设从出发起，运动了t秒，当P、Q两点运动的路程之和恰好等于梯形OABC周长一半，这时，直线PQ能否把梯形的面积也分成相等的两部分，如有可能，请求出t的值；如不可能，请说明理由。
