中考专项训练——函数在实际中的应用
函数在中考中具有重要的地位,近几年中考中出现很多与实际问题相结合的函数题目,注意实际问题和函数的转化。
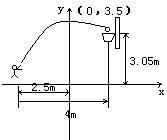
例1.如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05米。
(1)建立如图所示的直角坐标系,求抛物线的解析式。
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
分析:(1)已知,顶点(0,3.5)过一点(1.5,3.05)用顶点式。
(2)已知横坐标-2.5,求出纵坐标,就是抛出点的高度。
解:(1)由题意知抛物线顶点坐标为(0,3.5)且过(1.5,3.05)点,
∴设y=a(x-0)2+3.5
即y=ax2+3.5,
将(1.5, 3.05)代入,3.05=2.25a+3.5
2.25a=-0.45
a=-![]()
∴y=-![]() x2+3.5
x2+3.5
(2)当x=-2.5时,
y=-0.2×(-2.5)2+3.5=2.25
2.25-1.8-0.25=0.20(m)
答:球出手时,他距离地面高度是0.20m。
说明:求抛物线的解析式时,一定要正确找到抛物线上的点,并注意根据坐标系的位置,确定坐标的符号。
例2.某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中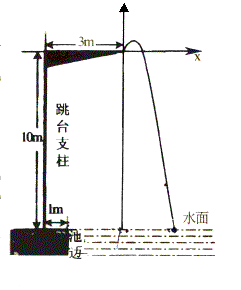 的运动路线是如图所示坐标系上经过原点O的一条抛物线(图中标出的数据为已知条件)。
的运动路线是如图所示坐标系上经过原点O的一条抛物线(图中标出的数据为已知条件)。
在跳某个规定动作时,正常情况下,该运动员在空中的最高处距离水面10![]() 米,入水处距池边的距离为4m,同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
米,入水处距池边的距离为4m,同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误。
(1)求这条抛物线的解析式。
(2)在某次试跳中,测得运动员在空中的运动路线是图中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3![]() m,问此次跳水会不会失误?并通过计算说明理由。
m,问此次跳水会不会失误?并通过计算说明理由。
分析:挖掘已知条件,由已知条件和图形可以知道抛物线过(0,0)(2,-10),顶点的纵坐标为![]() 。
。
解:(1)如图,在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为y=ax2+bx+c
由题意知,O、B两点的坐标依次为(0,0)(2,-10),且顶点A的纵坐标为![]() 。
。
∴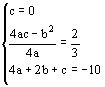 ∴
∴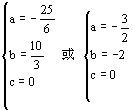
∵抛物线对称轴在y轴右侧,
∴![]() >0,
>0,
又∵抛物线开口向下,∴a<0,
b>0,
∴a=-![]() ,b=
,b=![]() ,c=0
,c=0
∴抛物线的解析式为:y=-![]() x2+
x2+![]() x
x
(2)当运动员在空中距池边的水平距离为3![]() 时,即x=3
时,即x=3![]() -2=
-2=![]() 时,
时,
 y=(-
y=(-![]() )×(
)×(![]() )2+
)2+![]() ×
×![]() =-
=-![]() ,
,
∴此时运动员距水面高为:10-![]() =
=![]() <5,
<5,
因此,此次试跳会出现失误。
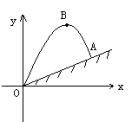
例3. (香港)今有网球从斜坡O点外抛出,网球的抛物路线方程是y=4x-![]() x2,
斜坡的方程是y=
x2,
斜坡的方程是y=![]() x,其中y是垂直高度(米),x是与O点的水平距离(米)
x,其中y是垂直高度(米),x是与O点的水平距离(米)
(1)网球落地时撞击斜坡的落点为A,写出A点的垂直高度,以及A点与O点的水平距离。
(2)在图象中,标出网球所能达到的最高点B,并求OB与水平线OX之间夹角的正切。
分析:(1)实际上是求A点的坐标;(2)求出顶点坐标是关键。
解:由方程组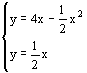 , ∴
, ∴![]()
∴ A(7,3.5)
∴ A点的垂直高度为3.5米,A点与O点的水平距离为7米。
(2)由y=4x-![]() x2=-
x2=-![]() (x-4)2+8
(x-4)2+8
∴ B(4,8), tanα=![]() =2.
=2.
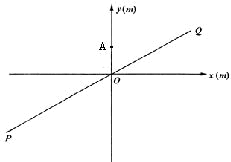
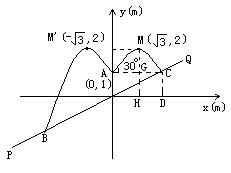
例4.已知斜坡PQ的坡度i=1∶![]() ,在坡面上点O处有一根1m高且垂直于水平面的水管OA,顶端A处有一旋转式喷头向外喷水,水流在各个方向沿相同的抛物线落下,水流的最高点M比点A高出1m,且在点A测得点M的仰角为30°,以O为原点,OA所在直线为y轴,过点O垂直于OA的直线为x轴建立坐标系,求水喷到斜坡上的最低点B与最高点C的距离。
,在坡面上点O处有一根1m高且垂直于水平面的水管OA,顶端A处有一旋转式喷头向外喷水,水流在各个方向沿相同的抛物线落下,水流的最高点M比点A高出1m,且在点A测得点M的仰角为30°,以O为原点,OA所在直线为y轴,过点O垂直于OA的直线为x轴建立坐标系,求水喷到斜坡上的最低点B与最高点C的距离。
分析:直线PQ是正比例,需一个条件确定k,用i=1∶![]() ,求线段BC应求出B、C坐标,即抛物线与直线交点。
,求线段BC应求出B、C坐标,即抛物线与直线交点。
解:过M作MH⊥x轴于H,过A作AG⊥MH于G,
 Rt△AGM中,∠MAG=30°,MG=1,∴AG=
Rt△AGM中,∠MAG=30°,MG=1,∴AG=![]() ,MH=2,
,MH=2,
∴M(![]() ,2)
,2)
∵M′与M点关于y轴对称,
∴M′(-![]() ,2),
,2),
 设以M为顶点的抛物线解析式为y=a(x-
设以M为顶点的抛物线解析式为y=a(x-![]() )2+2
)2+2
以M′为顶点的抛物线解析式为
y′=a′(x+![]() )2+2
)2+2
∵均过A(0,1),
∴a=-![]() ,a′=-
,a′=-![]() ,
,
∴y=-![]() x2+
x2+![]() x+1
x+1
y′=-![]() x2-
x2-![]() x+1,
x+1,
设直线PQ的解析式为y=kx,
∵i=1∶![]() ,C在PQ上,∴设C(
,C在PQ上,∴设C(![]() m,
m),
m,
m),
∴m=![]() mk,∴k=
mk,∴k=![]() ,
,
∴y=![]() x,
x,
∴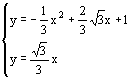 ∴C(
∴C(![]() )舍去负值。
)舍去负值。
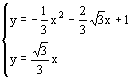 ∴B(
∴B(![]() )舍去正值。
)舍去正值。
∴CD=![]() ,OC=2CD=1+
,OC=2CD=1+![]()
OB=2![]() =3+
=3+![]() ,
,
∴BC=4+![]() +
+![]() 。
。
例5.(1)一辆宽2米的货车要通过跨度为8米,拱高为4米的单行抛物线隧道(从正中通过),为保证安全,车顶离隧道顶部至少要0.5米的距离,求货车的限高为多少?
(2)若将(1)中的单行道改为双行道,即货车必须从隧道中线的右侧通过,求货车的限高应是多少?
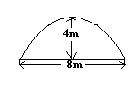
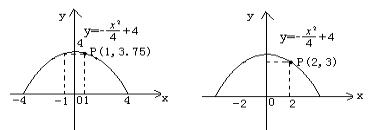
分析:题中已知条件有一条抛物线,要确定这条抛物线必须建立适当的坐标系。为使计算量小,可以过抛物线的对称轴建立坐标系。
解:建立如图所示坐标系,∵抛物线的顶点坐标是(0,4),∴可设抛物线的方程为y=ax2+4.
又抛物线过(4,0)点,∴
0=a×42+4,
∴ a=-![]() .
.
∴ y=-![]() x2+4
(-4≤x≤4)
x2+4
(-4≤x≤4)
(1)当x=1时,y=3.75.
∴货车限高为3.75-0.5=3.25(m)
(2)当x=2时,y=3
故货车限高为3-0.5=2.5米。
例6.一个运动员推铅球,铅球刚出手时离地面1![]() 米,铅球落地点距离铅球刚出手时相应的地面上的点10米,铅球运行中最高点离地面3米,已知铅球走过的路线是抛物线,求这个抛物线的解析式。
米,铅球落地点距离铅球刚出手时相应的地面上的点10米,铅球运行中最高点离地面3米,已知铅球走过的路线是抛物线,求这个抛物线的解析式。
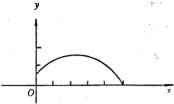
分析:这是一个物理问题,由于铅球的运动路线是抛物线,因此要运用二次函数的知识去解决问题。
解:根据题意,建立直角坐标系,如图
可知抛物线经过(0, ![]() )和(10, 0);抛物线顶点的纵坐标为3,根据题意,
)和(10, 0);抛物线顶点的纵坐标为3,根据题意,
设抛物线的解析式为y=a(x-h)2+3
(0≤x≤10)
将(0, ![]() )和(10, 0)代入解析式,得
)和(10, 0)代入解析式,得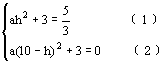
由①,得a=-![]() ,
,
代入②,得-![]() (10-h)2+3=0
(10-h)2+3=0
去分母,整理得h2+16h-80=0
解出h1=-20,
h2=4
当h=-20时,y=a(x+20)2+3,抛物线顶点为(-20, 3),此时当x=-20时,铅球运行中的最高点为3米,不符合
0≤x≤10的要求,舍去。
当h=4时,a=-![]() ,抛物线的解析式为y=-
,抛物线的解析式为y=-![]() (x-4)2+3
(x-4)2+3
即y=-![]() x2+
x2+![]() x+
x+![]() (0≤x≤10)。
(0≤x≤10)。
例7.A市场和B市场分别有库存某种机器12台和6台,现决定支援给C市10台,D市8台,已知从A市调运一台机器到C市、D市的运费分别为4百元和8百元;从B市调运一台机器到C市、D市的运费分别为3百元和5百元。
(1)设B市运往C市机器x台,求总运费W关于x的函数关系式;
(2)若要求总运费不超过9千元,问共有几种调运方案?
(3)求出总运费最低的调运方案,最低运费是多少元?
分析:本题属于规划调运问题,根据题意可建立问题的函数模型,讨论自变量的取值范围,并由函数的性质,讨论问题的最小值,本题是函数知识的灵活运用。
解:(1)因为B市场运往C市机器x台,所以B市场运往D市(6-x)台,A市运往C市(10-x)台,A市场运往D市(2+x)台;运费依次为:3x百元、5(6-x)百元、4(10-x)百元、8(2+x)百元.
总运费为W=3x+5(6-x)+4(10-x)+8(2+x)=2x+86
所求函数的表达式为W=2x+86
(2)由题意,得2x+86≤90,
∴x≤2
又∵B市可总共支援外地6台,
∴0≤x≤6,
∴0≤x≤2,故x可取0、1、2三个数,
所以要求总运费不超过9千元,共有三种调运方案。
(3)∵0≤x≤2,由一次函数性质,得
当x=0时,W的值最小,W最小值=86,
此时的调运方案是
B市场运至C市0台,运至D市6台;
A市场运至C市10台,运至D市2台。
最低总运费为8600元。
