我的小屋更多精彩http://www.xsj21.com/homepage.php?id=44139
2006年中考综合模拟试卷(一)
一、选择题(本题共24分,每小题4分)
1.下列各组数中,互为相反数的是( )
(A)2与![]() (B)
(B)![]() 与1 (C)-1与
与1 (C)-1与![]() (D)2与-2
(D)2与-2
2.为了迎接2008年奥运会在中国北京举行,北京市现在执行严格的机动车尾汽排放标准,同时正在设法减少工业及民用燃料所造成的污染,随着每年10亿立方米的天然气输送到北京,这样,到2006年底,北京的空气质量将会基本达到发达国家城市水平,10亿用科学记数法可以表示为( )
(A) 1.0×10![]() (B) 1.0×10
(B) 1.0×10![]() (C) 1.0×10
(C) 1.0×10![]() (D) 1.0×10
(D) 1.0×10![]()
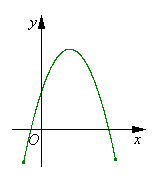
3.二次函数![]() 图象的大致位置如图,下列判断错误的是( )
图象的大致位置如图,下列判断错误的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.下列调查,比较容易用普查方式的是( )
(A)了解贵阳市居民年人均收入 (B)了解贵阳市初中生体育中考的成绩
(C)了解贵阳市中小学生的近视率 (D)了解某一天离开贵阳市的人口流量
5.下列图形中是轴对称图形,而不是中心对称图形的是( )
(A)等腰梯形 (B)矩形 (C)平行四边形 (D)菱形
6.给出下列四个命题:
(1)如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
(2)若点A在直线y=2x-3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
(4)若A(a,m)、B(a –1,n)(a![]() 0)在反比例函数
0)在反比例函数![]() 的图象上,则m
的图象上,则m![]() n.
n.
其中,正确命题的个数是( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
二、填空题(本题共24分,每小题4分)
7.分解因式:![]() =____________________.
=____________________.
8.函数![]() 自变量
自变量![]() 的取值范围是______________.
的取值范围是______________.
9.写一个两实数根和为2的一元二次方程为______________.
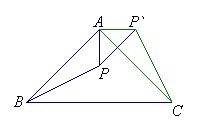
10.如图ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′有长等于____________.
11.为了估计湖里有多少条鱼,我们从湖里捕上100条做上标记,然后放回湖里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计湖里有鱼 ________条.
12.借助计算器探索:![]() =__________,
=__________,![]() =__________,猜想:
=__________,猜想:![]() =____________.
=____________.
三、解答题(本题共30分,每小题5分)
13.计算:
![]() +
+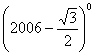
![]() tan60°.
tan60°.
14.解不等式组 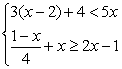
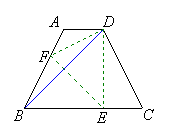
15.如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,
求:(1)BE的长;(2)∠CDE的正切值.
16.已知反比例函数![]() 与一次函数
与一次函数![]() 的图像的一个交点的纵坐标是
-4,求
的图像的一个交点的纵坐标是
-4,求![]() 的值.
的值.
17.已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.

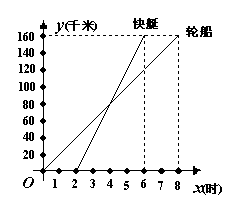
18.如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像(分别是正比例函数图像和一次函数图像).根据图像解答下列问题:
(1)根据图象,轮船比快艇早出发_______小时.
(2)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(3)通过计算说明快艇出发多长时间赶上轮船?
四、解答题(本题共20分,第19、21题各5分,第20题4分,第22题6分)
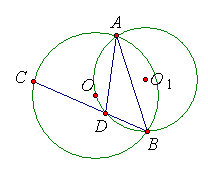
19.已知:如图,⊙O与⊙O1交于A和B两点,且O在⊙O1上,⊙O的弦BC交⊙O1于D.求证;AD=DC.
20.某工程队(有甲、乙两组)承包我市新区某路段的路基改造工程,规定若干天内完成.已知甲组单独完成这项工程所需时间比规定时间的2倍多4天,乙组单独完成这项工程所需时间比规定时间的2倍少16天.如果甲、乙两组合做24天完成,那么甲、乙两组合做能否在规定时间内完成?
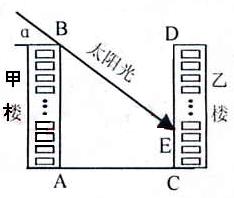
21.下图为某小区的两幢10层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
22.某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
|
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总分相等.此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率.
(2)求两班比赛数据的中位数.
(3)计算两班比赛数据的方差并比较.
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
五、解答题(本题共22分,第23题6分,第24题8分,第25题8分)
23.某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?

24.用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
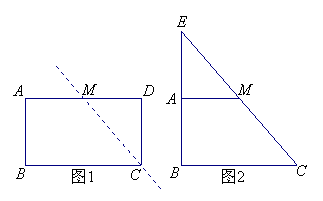
(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
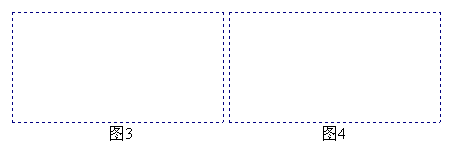
(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程![]() 的两个实数根,试求出原矩形纸片的面积.
的两个实数根,试求出原矩形纸片的面积.
25.已知二次函数![]() 当b取任何实数时,它的图象是一条抛物线.
当b取任何实数时,它的图象是一条抛物线.
(1)现在有如下两种说法:
错误!未找到引用源。b取任何不同的数值时,所对应的抛物线都有着完全相同的形状;
错误!未找到引用源。b取任何不同的数值时,所对应的抛物线都有着不相同的形状;你认为哪一种说法正确,为什么?
(2)若取b= -1,b=2时对应的抛物线的顶点分别为A、B,请你求出AB的解析式,并判断:当b取其它实数值时,所对应的抛物线的顶点是否在这条直线上?说明理由.
(3)在(2)中所确定的直线上有一点C且点C的纵坐标为-1,问在x轴上是否存在点D使△COD为等腰三角形,若存在直接写出点D坐标;若不存在,简单说明理由.
试题分析及解题过程
一、选择题(本题共24分,每小题4分)
1.下列各组数中,互为相反数的是( )
(A)2与![]() (B)
(B)![]() 与1 (C)-1与
与1 (C)-1与![]() (D)2与-2
(D)2与-2
点拨:相反数、倒数、绝对值是基本的知识点.
解答:C
2.为了迎接2008年奥运会在中国北京举行,北京市现在执行严格的机动车尾汽排放标准,同时正在设法减少工业及民用燃料所造成的污染,随着每年10亿立方米的天然气输送到北京,这样,到2006年底,北京的空气质量将会基本达到发达国家城市水平,10亿用科学记数法可以表示为( )
(A) 1.0×10![]() (B) 1.0×10
(B) 1.0×10![]() (C) 1.0×10
(C) 1.0×10![]() (D) 1.0×10
(D) 1.0×10![]()
点拨:10亿==1.0×10![]()
解答:C
3.二次函数![]() 图象的大致位置如图,下列判断错误的是( )
图象的大致位置如图,下列判断错误的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()

点拨:开口向下说明![]() ;与
;与![]() 轴的交点在
轴的交点在![]() 轴的上方,说明
轴的上方,说明![]() ;对称轴在
;对称轴在![]() 轴的右边,说明
轴的右边,说明![]() .
.
解答:D
4.下列调查,比较容易用普查方式的是( )
(A)了解贵阳市居民年人均收入 (B)了解贵阳市初中生体育中考的成绩
(C)了解贵阳市中小学生的近视率 (D)了解某一天离开贵阳市的人口流量
点拨:调查分为普查和抽样调查,采取普查方式的一定是能够操作的,调查对象相对固定,数量也比较小.
解答:B
5.下列图形中是轴对称图形,而不是中心对称图形的是( )
(A)等腰梯形 (B)矩形 (C)平行四边形 (D)菱形
点拨:轴对称、中心对称在新的课标下对于学生建立对图像的感觉有非常重要的意义,体会图形的平移、旋转和轴对称,对于让学生用运动的观点去理解全等、相似等有非常重要的意义.
解答:A
6.给出下列四个命题:
(1)如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
(2)若点A在直线![]() 上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
(3)半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
(4)若A(a,m)、B(a –1,n)(a![]() 0)在反比例函数
0)在反比例函数![]() 的图象上,则m
的图象上,则m![]() n.
n.
其中,正确命题的个数是( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
点拨:(1)设底面半径是![]() ,母线长是
,母线长是![]() ,则
,则![]() ,即
,即![]() ,直角边等于斜边的一半,所以轴截面是一个等边三角形;(2)A点到两轴的距离相等,可设它的坐标是(
,直角边等于斜边的一半,所以轴截面是一个等边三角形;(2)A点到两轴的距离相等,可设它的坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),A点在
),A点在![]() 上,则有
上,则有![]() 或
或![]() ,所以
,所以![]() 或
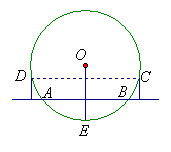
或![]() ,A点的坐标就是(3,3)或(1,-1);(3)如图,到AB距离等于2的是D、C、E三点;(4)当
,A点的坐标就是(3,3)或(1,-1);(3)如图,到AB距离等于2的是D、C、E三点;(4)当![]() 时,
时,![]() ,
,![]() 结论错误.
结论错误.
解答:B
二、填空题(本题共24分,每小题4分)
7.分解因式:![]() =____________________.
=____________________.
点拨:四项式的分解因式需要进行适当的分组,分组的原则是:首先看有没有能够构成完全平方的项,然后看看有没有能够构成平方差的项,最后看有没有公因式.本题前三项能够构成完全平方,所以它们应该分成一组,即:![]()
![]() ,然后做平方差.
,然后做平方差.
解答:![]()
8.函数![]() 自变量
自变量![]() 的取值范围是______________.
的取值范围是______________.
点拨:函数自变量的取值范围就是使代数式有意义的条件。本题中的代数式不仅有被开方数,而且有分母,所以![]() .
.
解答:![]()
9.写一个两实数根和为2的一元二次方程为______________.
点拨:本题考查学生对根系关系和根的判别式的灵活运用,构造出来的方程一定要注意是否有实数根.比如方程![]() 就满足条件,而方程
就满足条件,而方程![]() 就没有实数根.
就没有实数根.
解答:不唯一
10.如图ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′有长等于____________.

点拨:本题是考查平移旋转的有关知识,易知AP=3,AP`=3,∠PAP`=90º,所以PP`=![]()
解答:![]()
11.为了估计湖里有多少条鱼,我们从湖里捕上100条做上标记,然后放回湖里,经过一段时间待带标记的鱼完全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,通过这种调查方式,我们可以估计湖里有鱼 ________条.
点拨:统计方面的试题成为中考比重增加较快的一个知识点,由于它与实际生活的紧密联系,让学生更能体会学习的乐趣.本题是一个概率方面的问题,200条中有25条做过标记的鱼,说明比例是8∶1,有100条做过标记,所以总共的鱼数是800.
解答:800.
12.借助计算器探索:![]() =__________,
=__________,![]() =__________,猜想:
=__________,猜想:![]() =____________.
=____________.
点拨:计算器的使用成为中考的一个热点,本题通过试验能够很快发现他们的规律.
解答:555,55555,![]()
三、解答题(本题共30分,每小题5分)
13.计算:
![]() +
+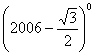
![]() tan60°.
tan60°.
点拨:零次幂、负整数次幂、锐角三角函数都是学生需要掌握的基本运算.
解答:-1
14.解不等式组 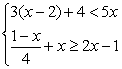
点拨:不等式及不等式组有着广泛的应用,与许多的知识点有关联,比如函数,比如实际应用型的问题的解决等.
解答:![]()
15.如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8,
求:(1)BE的长;(2)∠CDE的正切值.

点拨:翻折始终是考试的一个热点,它实际轴对称的运用,而新课标对学生动手能力和实际操作能力的重视使得这个题型还会热下去.
解答:(1)∵∠DBC=45°∴∠EDB=45°,∴DE⊥BC,∵ABCD是等腰梯形,∴EC=3,BE=5;(2)∵DE=BE=5,CE=3,∴∠CDE=![]() .
.
16.已知反比例函数![]() 与一次函数
与一次函数![]() 的图像的一个交点的纵坐标是
-4,求
的图像的一个交点的纵坐标是
-4,求![]() 的值.
的值.
点拨:反比例函数和一次函数是函数思想的入门,用待定系数法求函数的解析式也是函数中非常重要的方法.
解答:根据题意有
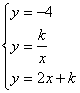 ,所以
,所以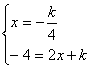 解得
解得![]() .
.
17.已知:如图,矩形ABCD中,AC与BD交于O点,若点E是AO的中点,点F是OD的中点.求证:BE=CF.

点拨:此题包含的知识点有:矩形的性质、中点的性质、图形全等的判定、图形全等的性质,重在考查学生的基本逻辑思维能力.
解答:∵ABCD是矩形,∴OA=OB=OC=OD,又∵点E是AO的中点,点F是OD的中点,∴OE=OF(等量的等分量相等),在△BEO与△CFO中∵ ∴△BEO≌△CFO,∴BE=CF.
∴△BEO≌△CFO,∴BE=CF.
18.如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图像(分别是正比例函数图像和一次函数图像).根据图像解答下列问题:
(1)根据图象,轮船比快艇早出发_______小时.
(2)请分别求出表示轮船和快艇行驶过程的函数解析式(不要求写出自变量的取值范围);
(3)通过计算说明快艇出发多长时间赶上轮船?

点拨:识图是新课标重点强调的学生的一种基本能力,根据题意画出图像,和由图像读出相关的信息都是对函数知识的灵活运用.
解答:(1)2;(2)轮船行驶过程是一条经过原点的直线,由图形可知它还经过(8,160),设函数解析式是![]() ,解得
,解得![]() ,所以解析式是
,所以解析式是![]() ;快艇的行驶过程经过了两点(2,0),(6,160),设它的解析式是
;快艇的行驶过程经过了两点(2,0),(6,160),设它的解析式是![]() ,解得:
,解得:![]() ,所以解析式是
,所以解析式是![]() .(3)求出两条直线的交点就可以知道何时赶上轮船.交点是(4,80),所以快艇出发2个小时后追上轮船.
.(3)求出两条直线的交点就可以知道何时赶上轮船.交点是(4,80),所以快艇出发2个小时后追上轮船.
四、解答题(本题共20分,第19、21题各5分,第20题4分,第22题6分)
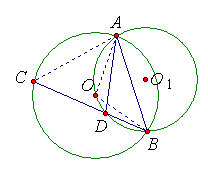
19.已知:如图,⊙O与⊙O1交于A和B两点,且O在⊙O1上,⊙O的弦BC交⊙O1于D.求证;AD=DC.

点拨:圆的有关知识依然是初中几何的集中体现,许多的知识都可以包含在圆的有关知识中,本题所包含的知识点有:公共弦、圆周角与圆心角、三角形的外角、等腰三角形的性质.
解答:(如图)连接AC、AO、BO.∠ADB=∠AOB=2∠C,∠ADB=∠C+∠DAC,所以∠C=∠DAC,则AD=DC.
20.某工程队(有甲、乙两组)承包我市新区某路段的路基改造工程,规定若干天内完成.已知甲组单独完成这项工程所需时间比规定时间的2倍多4天,乙组单独完成这项工程所需时间比规定时间的2倍少16天.如果甲、乙两组合做24天完成,那么甲、乙两组合做能否在规定时间内完成?
点拨:方程的应用是中考中的保留题型,方程的思想以及体现数学在实际生活中的应用都需要把这样的应用题继续作为中考的重点试题.
解答:设规定的时间是![]() 天,则甲组单独完成所需要的时间是
天,则甲组单独完成所需要的时间是![]() 天,乙组单独完成所需的时间是
天,乙组单独完成所需的时间是![]() 天,可得:
天,可得:![]() ,解得:
,解得:![]() ,经检验
,经检验![]() 不符合题意,舍去.所以规定的时间是28天,它们两组能够在规定的时间内完成这项工作.
不符合题意,舍去.所以规定的时间是28天,它们两组能够在规定的时间内完成这项工作.
21.下图为某小区的两幢10层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.

点拨:让学生体会数学的乐趣,就需要让学生感受到数学在实际生活的应用,解直角三角形的应用,是初中几何中最接近实际问题的知识点.
解答:(1)![]() (2)当α=30°时,
(2)当α=30°时,![]() ,落在第五层;当α=45°时,甲楼的影子刚好不影响乙楼采光,所以需要1.5小时.
,落在第五层;当α=45°时,甲楼的影子刚好不影响乙楼采光,所以需要1.5小时.
22.某校初三学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
|
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总分相等.此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率.
(2)求两班比赛数据的中位数.
(3)计算两班比赛数据的方差并比较.
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
点拨:统计方面的知识在新的课标下得到发展,它是数学与实际生活接触最紧密的一章,也是培养学生的数学兴趣非常有用的平台.最近几年在各个地方的中考中,这方面的试题都在逐渐加重.
解答:(1)甲班的优秀率是60%,乙班的优秀率是40%;(2)甲班的中位数是100,乙班的中位数是97;(3)甲班的方差是![]() ,乙班的方差是
,乙班的方差是![]() ,乙班的方差较大,说明乙班的波动比较大.(4)冠军应该是甲班,首先是优秀率高于乙班,其次中位数较大,而且甲班的方差较小,说明它们的成绩波动较小.
,乙班的方差较大,说明乙班的波动比较大.(4)冠军应该是甲班,首先是优秀率高于乙班,其次中位数较大,而且甲班的方差较小,说明它们的成绩波动较小.
五、解答题(本题共22分,第23题6分,第24题8分,第25题8分)
23.某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?

点拨:有关二次函数应用的试题是中考比较热点的知识点.本题涉及的知识点有:待定系数法求函数的解析式,点是否在函数图像上。同时还需要将实际问题转化为数学问题的能力.
解答:(1)有题意可知,抛物线经过(0,![]() ),顶点坐标是(4,4).设抛物线的解析式是
),顶点坐标是(4,4).设抛物线的解析式是![]() ,解得
,解得![]() ,所以抛物线的解析式是
,所以抛物线的解析式是![]() ;篮圈的坐标是(7,3),只要这个点在抛物线上,球就能够投中.代入解析式得
;篮圈的坐标是(7,3),只要这个点在抛物线上,球就能够投中.代入解析式得![]() ,所以能够投中.(2)能够获得成功就要看1m处得纵坐标是多少,大于3.1就不能成功。当
,所以能够投中.(2)能够获得成功就要看1m处得纵坐标是多少,大于3.1就不能成功。当![]() 时,
时,![]() ,所以能够盖帽拦截成功.
,所以能够盖帽拦截成功.
24.用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.

(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.

(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程![]() 的两个实数根,试求出原矩形纸片的面积.
的两个实数根,试求出原矩形纸片的面积.
点拨:培养学生动手超作的能力是新课程标准的新的要求,图形的平移、旋转能够产生许多美丽的图案,让学生享受其中,提高对数学学习的兴趣。本题有很好将几何问题与一元二次方程的有关知识结合在一起,考查了学生综合运用知识解决问题的能力.
解答:(1)如图:
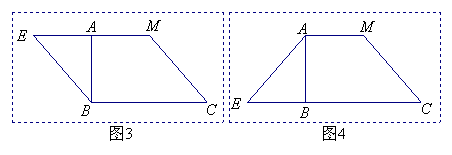
(2)Rt△BCE是等腰直角三角形,所以![]() ;
;
a、b恰好是关于x的方程![]() 的两个实数根,
的两个实数根,
所以![]() ,可得:
,可得:![]() 代入
代入![]() 解得:
解得:![]() .当
.当![]() 时,
时,![]() 不符合实际情况,所以
不符合实际情况,所以![]() ,解得:
,解得:![]() .
.
25.已知二次函数![]() 当b取任何实数时,它的图象是一条抛物线.
当b取任何实数时,它的图象是一条抛物线.
(1)现在有如下两种说法:
错误!未找到引用源。b取任何不同的数值时,所对应的抛物线都有着完全相同的形状;
错误!未找到引用源。b取任何不同的数值时,所对应的抛物线都有着不相同的形状;你认为哪一种说法正确,为什么?
(2)若取b= -1,b=2时对应的抛物线的顶点分别为A、B,请你求出AB的解析式,并判断:当b取其它实数值时,所对应的抛物线的顶点是否在这条直线上?说明理由.
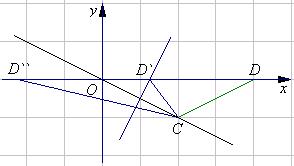
(3)在(2)中所确定的直线上有一点C且点C的纵坐标为-1,问在x轴上是否存在点D使△COD为等腰三角形,若存在直接写出点D坐标;若不存在,简单说明理由.
点拨:二次函数的综合运用是初中知识中能够体现数学思想和数学方法的平台,分类讨论思想是这种题型中非常重要的一种.
解答:(1)抛物线的形状和开口方向只决定于二次项系数的值,与一次项的系数、常数项无关.所以①的说法是正确的。(2)当b= -1时,顶点坐标是A(![]() ,
,![]() );当b= 2时,顶点坐标是B(
);当b= 2时,顶点坐标是B(![]() ,
,![]() ),所以直线AB的解析式是
),所以直线AB的解析式是![]() .二次函数
.二次函数![]() 的顶点坐标可以表示为(
的顶点坐标可以表示为(![]() ,
,![]() ),它们始终在直线
),它们始终在直线![]() 上.(3)如图,存在三个满足条件的点,它们的坐标分别是(4,0),(
上.(3)如图,存在三个满足条件的点,它们的坐标分别是(4,0),(![]() ,0),(
,0),(![]() ,0).
,0).
试卷的整体评价
1.知识点覆盖率:90%
2.考查重点:数学基础知识、数学知识的应用、数学的计算能力、分析能力、逻辑思维能力.
3.规律总结:题型更新,应用加强.
4.2006年中考预测:阅读理解型题、探索性题型、应用型题型、分类讨论性题型、运动型题目应该是这一年中考的重点试题,继续重视数学基础,继续要求学生的数学能力.考查学生的数学思想方法,检测学生的数学知识综合运用的能力,仍然是中考命题的重要任务.
5.复习对策:数学复习不是简单的内容再现和重复,而是对知识的整理、疏通,升华,教会学生驾驭教材,掌握知识、灵活应用.中考数学新题型虽背景新颖,千变万化,但万变不离其本—课本.课本是新题型的直接来源,课本是解题能力的生长点.由于新题型是能力型试题,因此中考对新题型的复习必须把能力的培养落实到位.中考复习必须帮助学生从总体上条理出解决问题的本质思路,引导学生抓住贯穿于各种类型问题的“红线”,即教学观点.复习过程中随时利用问题情境,帮助学生提炼教学观点,长此以往,学生在新题型面前,就能够迅速地从宏观上驾驭解题思路,再结合纯熟的“三基”就能够从微观上作出正确的解答.
总之,中考数学题是越来越难,越来越灵活,新型题目形式多样,涉及的知识面也越来越宽,不仅要求教师精通教材,有良好的数学素质,而且要教师博闻强识,了解生活的方方面面,随时利用问题情境,提炼教学观点,培养数学意识.