2005年临沂市中考试题(课改实验区用)
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分．第1卷l至4页，第Ⅱ卷5至12页．满分120分．考试时间120分钟．
第1卷(选择题 共42分)
注意事项：
1．答第1卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后。再选涂其它答案，不能答在试卷上。
3．考试结束，将本试卷和答题卡一并交回．
一、选择题(本题共14小题．每小题3分，共42分)在每小题所给的四个选项中，只有一项是符合题目要求的．
1．一3的绝对值是
(A)3
(C)±3 (B) 3 (D)±
2．2004年临沂市的国民生产总值为1012亿元，用科学记数法表示正确的是
(A)1012×10
元
(B)1.012×
元
(C)1.0×元． (D)1.012×
元．
3．下列各式计算正确的是
(A)
．(B)
(C)
(D)
。
4．一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球，从中随机摸出一个，摸到黄球的概率是
(A) 
(B) (C) 
(D) 
5．如图，将两根钢条
、
的中点O连在一起，使、可以绕着点0自由转动，就做成了一个测量工件，则
的长等于内槽宽AB，那么判定△AOB
△
的理由是
(A)边角边 (B)角边角 (C)边边边 (D)角角边
|
(A)r>2 (13)2<r<14 (C)l<r<8 (13)2<r<8
7．化简
的结果是
(A)一4
(B)4 (C)
(13)
+4
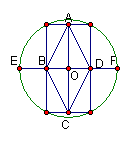8．如图，顺次连结圆内接矩形各边的中点，得到菱形ABCD，若BD＝10，DF＝4，则菱形ABCD的边长为
(A)4
．
(B)5
(C)6．
(D)9．
9．小华同学自制了一个简易的幻灯机，其工作情况如图所示，幻灯片与屏幕平行，光源到幻灯片的距离是30cm幻灯片到屏幕的距离是1.5m，幻灯片上小树的高度是10cm，则屏幕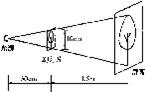
上小树的高度是
(A)50cm．
(B)500cm．
(C)60 cm．
(D)600cm．
|
(A)1个． (B)2个．
(C)3个． (D)4个．
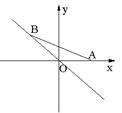11．如图，已知点A的坐标为(1，0)，点B在直线
上运动，当线段AB最短时，点B的坐标为
(A)(0，0)． (B)
．
(c) 
(D) 
．
12．等腰三角形一腰上的高与另一腰的夹角为30。，则顶角的度数为
(A)60
． (B)120． (C)60或150． (D)60或120
13．如图是无盖长方体盒子的表面展开图(重叠部分不计)，则盒子的容积为
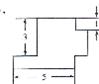(A)4．
(C)12．
(B)6．
(D)15
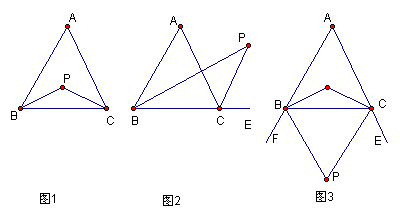
14．已知△ABC，
(1)如图l，若P点是
ABC和ACB的角平分线的交点，则P=
；
(2)如图2，若P点是ABC和外角ACE的角平分线的交点，则P=
；
(3)如图3，若P点是外角CBF和BCE的角平分线的交点，则P=
。
上述说法正确的个数是
(A)0个 (B)1个 (C)2个 (D)3个
2005年临沂市中考试题(课改实验区用)
第Ⅱ卷(非选择题 共78分)
注意事项：
1．第Ⅱ卷共8页，用钢笔或园珠笔直接答在试卷上。
2．答卷前将密封线内的项目及座号填写清楚。
二、填空题(本大题共5小题．每小题3分，共15分)把答案填在题中横线上．
15．关于
的不等式3一2
≤一2的解集如图所示，则的值是_______________。
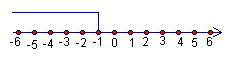
(第15题图)
16．若圆周角
所对弦长为sin，则此圆的半径r为___________。
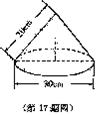
17．如图是小芳学习时使用的圆锥形台灯灯罩的示意图，则围成这个灯罩的铁皮的面积___________cm
。(不考虑接缝等因素，计算结果用
表示)
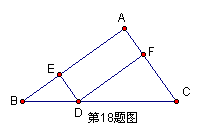
18．如图，Rt△ABC中，A＝90，AB＝4，AC＝3，D在BC上运动(不与B、C重合)，过D点分别向AB、Ac作垂线，垂足分别为E、F，则矩形AEDF的面积的最大值为___________。
19．判断一个整数能否被7整除，只需看去掉一节尾(这个数的末位数字)后所得到的数与此一节尾的5倍的和能否被7整除．如果这个和能被7整除，则原数就能被7整除．如126，去掉6后得12，12+6×5＝42，42能被7整除，则126能被7整除．类似地，还可通过看去掉该数的一节尾后与此一节尾的”倍的差能否被7整除来判断，则
___________（
是整数，且1≤n<7)．
三、开动脑筋．你一定能做对
20．(本小题满分6分)
为了了解家庭日常生活消费情况，小亮记录了他家一年中7周的日常生活消费费用．数据如下(单位：元)：
230 l 95 180 250 270 455 170
请你用统计初步的知识，计算小亮家平均每年(每年按52周计算)的日常生活消费总费用．
21．(本小题满分7分)
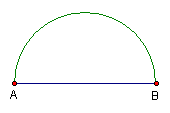
小芸在为班级办黑板报时遇到了一个难题，在版面设计过程中需将一个半圆面三等分，请你帮助她设计一个合理的等分方案．要求用尺规作出图形，保留作图痕迹，并简要写出作法．
22．(本小题满分8分)
某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖，装饰材料商场出售的这种瓷砖有大、小两种包装，大包装每包50片，价格为30元；小包装每包30片，价格为20元，若大、小包装均不拆开零售，那么怎样制定购买方案才能使所付费用最少?
四、认真思考，你一定能成功！
23．(本小题满分9分)
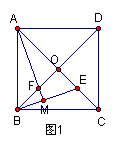
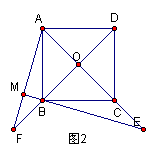
如图l，已知正方形ABCD的对角线AC、BD相交于点O，E是AC上一点，连结EB，过点A作AM
BE，垂足为M，AM交BD于点F．
(1)求证：OE=OF；
(2)如图2，若点E在AC的延长线上，AMBE于点M，交DB的延长线于点F，其它条件不变，则结论“OE=OF”还成立吗?如果成立，请给出证明；如果不成立，请说明理由．
24．(本小题满分10分)
某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
| 年 度 | 2001 | 2002 | 2003 | 2004 |
| 投入技改资金z(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本，(万元／件) | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
(2)按照这种变化规律，若2005年已投人技改资金5万元．
①预计生产成本每件比2004年降低多少万元?
②如果打算在2005年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元（结果精确到0.01万元)?
五、相信自己。加油呀
25．(本小题满分10分)
△ABC中，BC＝，AC＝
，AB＝c．若
，如图l，根据勾股定理，则
。若△ABC不是直角三角形，如图2和图3，请你类比勾股定理，试猜想
与
的关系，并证明你的结论．
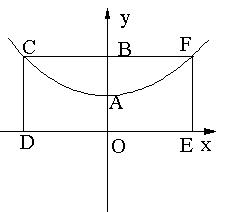
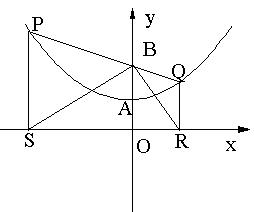
26．(本小题满分13分)
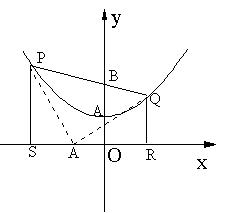
如图1，已知抛物线的顶点为A(O，1)，矩形CDEF的顶点C、F在抛物线上，D、E在轴上，CF交y轴于点B(0，2)，且其面积为8．
(1)求此抛物线的解析式；
(2)如图2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作轴的垂线，垂足分别为S、R．
①求证：PB＝PS；
②判断△SBR的形状；
③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似，若存在，请找出M点的位置；若不存在，请说明理由．
2005年临沂市中考试题(课改实验区用)
数学试题参考答案及评分标准
注：第三、四、五题给出了一种解法或两种解法．考生若用其它解法．应参照本评分标准给分
一、选择题(每小题3分，共42分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 答案 | A | B | D | C | A | D | A | D | C | C | B | D | B | C |
二、填空题(每小题3分．共15分l
1 5．一
； 16．； 17． 300； 18 ．3； 19 ．2。
三、开动脑筋，你一定能做对（共21分）
20．解：由题中7周的数据．可知小亮家平均每周日常生活消费的费用为：
(230+195+180+250+270+455+170)=250(元) …………（4分）
小亮家每年日常生活消费总赞用为：
250×52=13000(元)
答：小亮家平均每年的日常生活消费总费用约为13000元 …………… (6分)
2l．解：
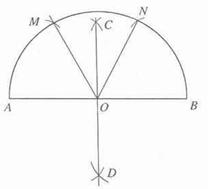
作法：
(1)作AB的垂直平分线CD交AB于点O；
(2)分别以A、B为圆心，以AO(或BO)的长为半径画弧，分别交半圆干点M、N；
(3)连结OM、ON即可．
说明：本小题满分7分。画图正确得4分；写出作法，每步各1分，共3分。
22．解：根据题意，可有三种购买方案；
方案一：只买大包装，则需买包数为：
；
由于不拆包零卖．所以需买10包．所付费用为30×10=300(元) … (1分)
方案二：只买小包装．则需买包数为：
所以需买1 6包，所付费用为1 6×20＝320(元) ……… (2分)
方案三：既买大包装．又买小包装，并设买大包装包．小包装
包．所需费用为W元。
则
…………（4分）
…………（5分）
∵
，且为正整数，
∴
9时，
290(元)．
∴购买9包大包装瓷砖和l包小包装瓷砖时，所付费用最少．为290元。
………………………………………………………………（7分）
答：购买9包大包装瓷砖和l包小包装瓷砖时，所付费用最少为290元。
……………………………………………………………… (8分)
四、认真思考．你一定能成功！(共19分)
23(1)证明：∵四边形ABCD是正方形．
∴BOE=AOF＝90．OB＝OA ……………… (1分)
又∵AMBE，∴MEA+MAE＝90=AFO+MAE
∴MEA＝AFO………………（2分）
∴Rt△BOE≌ Rt△AOF ……………… (3分)
∴OE=OF ………………(4分)
(2)OE＝OF成立 ……………… (5分)
证明：∵四边形ABCD是正方形，
∴BOE=AOF＝90．OB＝OA ……………… (6分)
又∵AMBE，∴F+MBF＝90=B+OBE
又∵MBF＝OBE
∴F＝E………………（7分）
∴Rt△BOE≌ Rt△AOF ……………… (8分)
∴OE=OF ………………(9分)
24．(1)解：设其为一次函数，解析式为
当
时，
；
当=3时，
6．
解得
，
∴一次函数解析式为
把
时，
代人此函数解析式，
左边≠右边．
∴其不是一次函数．
同理．其也不是二次函数． ………… (3分)
(注：学生如用其它合理的方式排除以上两种函数，同样得3分)
设其为反比例函数．解析式为
。
当时，，
可得
解得
∴反比例函数是
。………… (5分)
验证：当=3时，
，符合反比例函数。
同理可验证4时，，
时，
成立。
可用反比例函数表示其变化规律。………… (6分)
(2)解：①当5万元时，，
。………… (7分)
（万元），
∴生产成本每件比2004年降低0．4万元。………… (8分)
②当
时，
。
∴
………… (9分)
∴
（万元）
∴还约需投入0.63万元． …………… (10分)
五、相信自己，加油呀！（共23分）
25解：若△ABC是锐角三角形，则有
…… (1分)
若△ABC是钝角三角形，
为钝角，则有
。
(2分)
当△ABC是锐角三角形时，
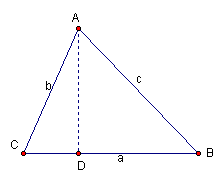
证明：过点A作ADBC，垂足为D，设CD为，则有BD＝
……（3分）
根据勾股定理，得
即
。
∴
…………………………（5分）
∵
，
∴
。
∴。…………………………（6分）
当△ABC是钝角三角形时，
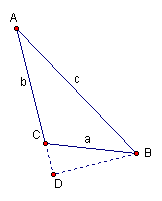
证明：过B作BDAC，交AC的延长线于D。
设CD为，则有
…………………………（7分）
根据勾股定理，得
．
即
。…………………………（9分）
∵
，
∴
，
∴。…………………………（10分）
26.⑴解：方法一：
∵B点坐标为(0．2)，
∴OB＝2，
∵矩形CDEF面积为8，
∴CF=4.
∴C点坐标为(一2，2)．F点坐标为(2，2)。
设抛物线的解析式为
．
其过三点A(0，1)，C(-2．2)，F(2，2)。
得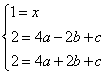
解这个方程组，得
∴此抛物线的解析式为 
………… (3分)
方法二：
∵B点坐标为(0．2)，
∴OB＝2，
∵矩形CDEF面积为8，
∴CF=4.
∴C点坐标为(一2，2)。 ……… (1分)
根据题意可设抛物线解析式为
。
其过点A(0，1)和C(-2．2)
………
解这个方程组，得
此抛物线解析式为
(2)解：
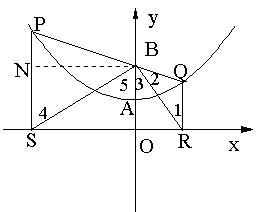
①过点B作BN
，垂足为N．
∵P点在抛物线y=
十l上．可设P点坐标为
．
∴PS＝
，OB＝NS＝2，BN＝。
∴PN=PS—NS=
………………………… (5分)
在Rt
PNB中．
PB＝
∴PB＝PS＝………………………… (6分)
②根据①同理可知BQ＝QR。
∴
，
又∵
，
∴
，
同理SBP＝
………………………… (7分)
∴
∴
∴
.
∴ △SBR为直角三角形．………………………… (8分)
③方法一：
设
，
∵由①知PS＝PB＝b．
，
。
∴
∴
。………………………… (9分)
假设存在点M．且MS＝，别MR＝
。
若使△PSM∽△MRQ，
则有
。
即
∴
。
∴SR＝2
∴M为SR的中点.………………………… (11分)
若使△PSM∽△QRM，
则有
。
∴
。
∴
。
∴M点即为原点O。
综上所述，当点M为SR的中点时．
PSM∽MRQ；当点M为原点时，PSM∽MRQ．………………………… (13分)
方法二：
若以P、S、M为顶点的三角形与以Q、M、R为顶点的三角形相似，
∵
，
∴有PSM∽MRQ和PSM∽△QRM两种情况。
当PSM∽MRQ时．SPM＝RMQ，SMP＝RQM．
由直角三角形两锐角互余性质．知PMS+QMR＝
。
∴
。………………………… (9分)
取PQ中点为N．连结MN．则MN＝PQ=
．…………………… (10分)
∴MN为直角梯形SRQP的中位线,
∴点M为SR的中点 …………………… (11分)
当△PSM∽△QRM时，
又
，即M点与O点重合。
∴点M为原点O。
综上所述，当点M为SR的中点时，PSM∽△MRQ；当点M为原点时，PSM∽△QRM……………………… (13分)