2005年中考数学模拟试题
(考试时间：120分钟，满分：150分)
请注意：1.本试卷分第一部分选择题和第二部分非选择题．
2.考生答卷前，必须将自己的姓名、考试号用黑色或蓝色钢笔或圆珠笔填写在试卷和答题卡的相应位置，再用2B铅笔将考试号、科目填涂在答题卡上相应的小框内．
第一部分 选择题（共36分）
请注意：考生必须将所选答案的字母标号用2B铅笔填涂到答题卡上相应的题号内，答在试卷上无效．
一、选择题（下列各题所给答案中,只有一个答案是正确的.每小题3分,共36分）
1、下列式子结果是负数的是（ ）
A. －
B. －(－3) C. 
D. 
2、如图，各“风车”型的平面图案中，是中心对称图形的个数为
A. 1 B.2 C.3 D.4
3．矩形的两邻边长分别为2.5和5，若以较长一边为直径作圆，则与圆相切的矩形的边共有
A. 4条 B. 3条 C. 2条 D. 1条
4．两个顶角相等的等腰三角形框架，其中一个三角形框架的腰长为6，底边长为4，另一个三角形的框架的底边长为2，则这个三角形框架的腰长为
A. 6 B. 5 C. 4 D. 3
5.下列图形中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开图的是:
6.以下是一些来自媒体的信息，你认为比较可信的数据是
A.报纸刊载：高校毕业生平均年收入为5万元．（数据来源于对某高校校友的一次问卷调查）
B.某房产广告称：本地区居民年收入6万元．（事实上该地区居住了许多普通工人家庭，只有几户富翁家庭）
C.某杂志刊载消息解释其价格上涨原因：10年来，原材料上涨10%，印刷费增加10%，推销广告费上升10%．这样一来，成本增加30%，零售价格也上涨了
D.据报载：我市中考体育加试报名时发现今年参加中考的学生人数比去年增长30%．
7．一张桌子上摆放着若干个碟子，从三个方向看，三种视图如下图所示,，则这张桌子上共有碟子为
A. 6个 B. 8个 C. 12个 D. 17个
8、在“抛一枚均匀硬币”的实验中，如果现在没有硬币，则下面各个试验中哪个不能代替
A. 两张扑克，“黑桃” 代替“正面”，“红桃” 代替“反面”
B. 两个形状大小完全相同，但一红一白的两个乒乓球
C. 扔一枚图钉
D. 人数均等的男生、女生，以抽签的方式随机抽取一人
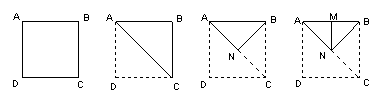9、将一张正方形的纸片按下图所示的方式三次折叠，折叠后再按图所示沿MN裁剪，则可得
A.
多个等腰直角三角形 B.
一个等腰直角三角形和一个正方形
C.两个相同的正方形 D. 四个相同的正方形
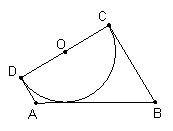
10．如图，已知梯形ABCD中，AD∥BC，∠C=900，以CD为直径的圆与AB相切，AB=6，那么梯形ABCD的中位线长是
A. 2 B. 3 C. 4
D. 不能确定，与∠B的大小有关
11、某出版社计划出版一套百科全书，固定成本为10万元，每印制一套需增加成本20元．如果该书以每套100元出售，卖出后需付书款的30%给承销商．若出版社要盈利10%，那么该书至少应发行（精确到千位）
A. 2千套 B. 3千套 C. 4千套 D. 5千套
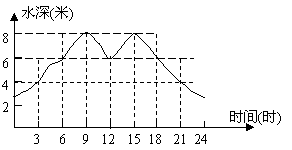12．一港口受潮汐影响，某天24小时内港内水深变化大致如下图．港口规定：为了保证航行安全，只有当船底与水底间的距离不少于4米时，才能进出该港．一艘吃水深度（即船底与水面的距离）为2米的轮船进出该港的时间最多为（单位：时）
| 座位号 |
A. 3 B. 6
C. 12 D. 18
第二部分 非选择题（共114分）
| 得分 | 评卷人 |
请注意：考生必须将答案直接做在试卷上
二、填空题（每题3分,共24分）
13．在实数—2，π，
，
中，无理数有______个
14．据报载：泰州市2004年国民经济生产总值(GDP)约为元，该数据用科学计数法表示为__________________元．
15．点(α，β)在反比例函数
的图象上，其中α、β是方程
的两根，则
．
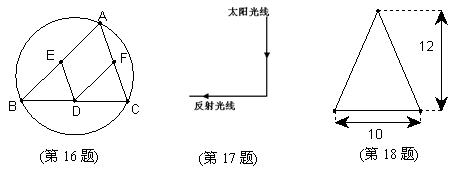16．如图，圆内接△ABC中，D是BC边的中点，E是AB边的中点，F是AC边的中点，连结DE、DF，要使四边形AEDF为菱形，应补充的一个条件是
．（只要填上一个你认为恰当的条件即可）
17．如图，一束光竖直照射在一平面镜上，如果要让反射光成水平光线，平面镜的镜面与入射光线的夹角应为 度．
18．如图是圆锥的主视图(单位：cm)， 其表面积为________cm2（结果保留π）
19．在一个不透明的布袋中放有除颜色外完全相同的三只小球，颜色分别为红、黑、白，任意摸出一球放回后再摸一球，则两次摸出的球颜色不同的概率为___________．
20．一个鞋厂有四个生产小组分别生产24厘米、24
厘米、25厘米、25厘米四种尺码的运动鞋，因故5月份只能有一组生产，其余三个小组暂停生产，为了确定哪个小组开工，工厂派出有关人员到商场查看最近一个月的销售记录，调查人员根据销售记录得到下列四种数据：①一个月售出运动鞋的总数②日平均销售数③一个月销售中四种尺码的众数④一个月的纯利润．你认为厂家应该最关心哪个数据_________（只填一个序号）
三、解答下列各题（第21、22、23、每题7分共21分）
21.计算：
22.先化简，再请你用喜爱的数代入求值
23.解不等式组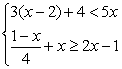 
四、生活中的数学（第24、25每题8分，第26题9分，27题10分,共35分）
24.某工程队（有甲、乙两组）承包我市新区某路段的路基改造工程，规定若干天内完成．已知甲组单独完成这项工程所需时间比规定时间的2倍多4天，乙组单独完成这项工程所需时间比规定时间的2倍少16天．如果甲、乙两组合做24天完成，那么甲、乙两组合做能否在规定时间内完成？
25. 2005年某学校学习小组分别调查了甲、乙两个小区居民的家庭人口数，并绘制了下面甲、乙的扇形统计图
（1）在甲图中，求出该小区居民家庭人口数的众数、中位数和平均数.
（2）学习小组的小明认为：乙小区中人口数为3人的居民家庭比甲小区中人口数为3人的居民家庭多，你认为合理吗，为什么？
 |
26.三等分角仪——把材料制成如图所示的阴影部分的形状，使AB与半圆的半径CB、CD相等，PB垂直于AD．这便做成了“三等分角仪”．如果要把∠MPN三等分时，可将三等分角仪放在∠MPN上，适当调整它的位置，使PB通过角的顶点P，使A点落在角的PM边上，使角的另一边与半圆相切于E点，最后通过B、C两点分别作两条射线PB、PC，则∠MPB=∠BPC=∠CPN．请用推理的方法加以证明．
 |
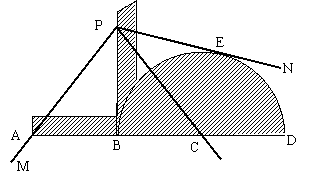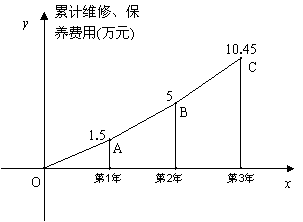
27.某企业投资100万元引进一条新产品加工线，若不计维修、保养费用，预计投产后每年可创利33万元，该生产线投产后，从第1年到第
年的维修、保养费用累计为
万元，其情况如下图所示，可以看出图中的折线近似于过原点的抛物线的一部分．
(1)求过O、A、B三点的的函数关系式；
(2)利用(1)的结果预测第4年的维修、保养费用，并说明第4年是否能收回投资并开始赢利．
五、试一试，想一想（第28题10分，第29题12分共22分）
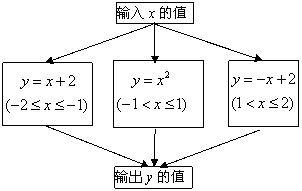
28．(02海淀区)如图所示的程序是函数型的数值转换程序，其中
．
(1)若输入的x值为
， 求输出的结果y,
(2)事件“输入任一符合条件的x，其输出的结果y是一个非负数”，是一个必然事件吗？说说你的理由．
(3)若所输入的x的值是满足条件的整数，求输出结果为0的概率．
 |
| 座位号 |
29．如图，在直角坐标系中，直线AB：
分别交x、y轴于点A、B，线段OA上的一动点C以每秒1个单位的速度由O向点A运动，线段BA上的一动点D以每秒
个单位的速度由B向A运动．
(1)在运动过程中△ADC与△ABO是否相似？试说明你的理由；
(2)问当运动时间t为多少秒时，以CD为直径的圆与y轴相切？
(3)在运动过程中是否存在某一时刻，使得△OCD与△ACD相似？若存在，求出运动时间；若不存在，说明理由．
 |
六、观察、探究、思考（本题满分12分）
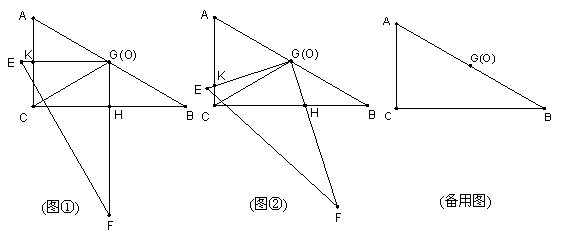
30．把两个全等的直角三角板ABC和EFG叠放在一起，使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，其中∠B＝∠F＝30°，斜边AB和EF长均为4．
(1)当 EG⊥AC于点K，GF⊥BC于点H时（如图①），求GH：GK的值
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转，旋转角α满足条件：0°＜α<30°（如图②），EG交AC于点K ，GF交BC于点H，GH：GK的值是否改变？证明你发现的结论；
(3)在②下，连接HK，在上述旋转过程中，设GH=，△GKH的面积为，求与之间的函数关系式，并写出自变量的取值范围；
（4）三角板EFG由图①所示的位置绕O点逆时针旋转一周，是否存在某位置使△BFG是等腰三角形，若存在，请直接写出相应的旋转角α(精确到0.1°)；若不存在，说明理由．
命题：张昕、吴志豪、刘振华
2005年中考数学模拟试题参考答案
一、选择题（每小题3分,共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | B | D | C | D | C | C | D | B | B | C |
二、填空题（每题3分,共24分）
13、1 14、7.05×1010
15、－8 16、AB＝AC（答案不唯一）
17、45° 18、90π
19、
20、③
三、21．－2 22、
，（x不能取0、2、4）
23．
四、24．规定天数为28天 ，大于24天，能在规定时间内完成。
25．(1)众数为3人、中位数为3人、平均数为3.2人
(2)不合理，可取反例说明：如甲小区中居民家庭人口数为200人，乙小区中居民家庭人口数为100人，……。
26． 简证：∵AB=AC，PB⊥AC
∴AP=AC
∴∠MPB=∠CPB
∵PB⊥BC且BC为半圆的直径，
∴PB为半圆的切线
又∵PN为半圆的切线
∴∠BPC=∠CPN
∴∠MPB=∠BPC=∠CPN
27． (1)
，(2)7.5万元，能(过程略)
28． (1)，(2)必然事件(过程略)，(3)
29．(1)相似，(2)1.2秒，(3)
或秒
30．(1)
，(2)不变，(3)
(
)，
(3)存在，30°、90°、133.2°或346.8°