2006年中考第一轮复习（三）一次函数
基础达标验收卷
一、选择题：
1.
（03杭州）一次函数
的图象不经过（ ）
A. 第一象限 B.
第二象限 C.
第三象限 D.
第四象限
2.
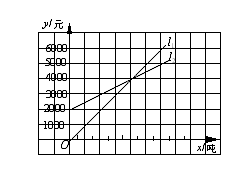
（04南宁）如图，
反映了某公司的销售收入与销售量的关系，
反映了该公司的产品销售成本与销售量的关系，当该公司赢利（收入大于成本）时，销售量（ ）
A. 小于3吨 B. 大于3吨
C. 小于4吨 D. 大于4吨
3.
（03哈尔滨）若正比例函数
的图象经过点
和点
，当
时，
，则m的 取值范围是（ ）
A. 
B.
C.
D.
4.
（03甘肃）结合正比例函数
的图象回答：当
时，y的取值范围是（ ）
A. 
B.1≤x<4 C.
D.
5.
（02山西）若
，则下列函数：①
；②
；③
；
④
中，y随x的增大而增大的是（ ）
A. ①② B. ②③ C. ①③ D. ③④
6.
（03河南）两条直线
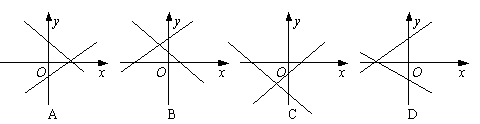
与
在同一坐标系中的图象可能是下图中的（ ）
7. （05黄冈）有一个装有进、出水管的容器，单位时间内进、出的水量都是一定. 已知容器的容积为600升，又知单开进水管10分钟可把空容器注满. 若同时打开进、出水管，20分钟可把满容器的水放完. 现已知容器内有水200升，先打开进水管5分钟，再打开出水管，两管同时开放，直至把容器中的水放完，则正确反映这一过程中容器中的水量Q（升）随时间t（分）变化的图象是（ ）
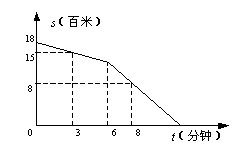
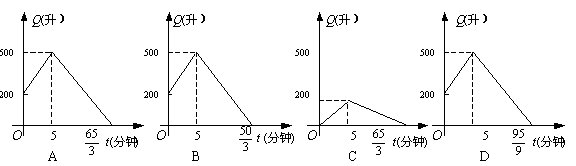
8. （05武汉）“高高兴兴上学来，开开心心回家去”小明某天放学后，17时从学校出发，回家途中离家的路程 s（百米）与所走的时间t（分钟）之间的函数关系如图所示，那么这天 小明到家的时间为（ ）
A. 17时15分 B. 17时14分
C. 17时12分 D. 17时11分
9.
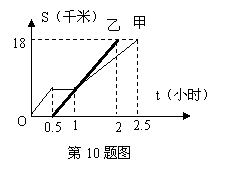（05陕西）甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系图象如图所示，根据图中提供的信息，有下列说法：
（1）他们都行驶了18千米；
（2）甲在途中停留了0.5小时；
（3）乙比甲晚出发了0.5小时；
（4）相遇后，甲的速度小于乙的速度；
（5）甲、乙两人同时到达目的地
其中符合图象描述的说法有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
二、填空题：
1. （03广州）如果正比例函数的图象经过点（2，1），那么这个函数的解析式是__________.
2.
（04四川）在平面直角坐标系中，直线
（k，b为常数k≠0，b>0）可以看成是将直线
沿y轴向上平行移动b个单位得到的，那么将直线沿x轴向右平行移动m个单位（m>0）得到的直线方程是____________.
3. （04大连）大连市内与庄河两地之间的距离是160千米，若汽车以平均每小时80千米的速度从大连开往庄河，则汽车距庄河的路程s（千米）与行驶的速度t（小时）之间的函数关系式为_________________.
4.
（03河南）若一次函数
的图象经过第一、二、四象限，则m的取值范围是________________.
三、解答题：
1.
已知y与
成正比例，且
时，
.
（1）求y与x之间的函数关系式；
（2）若点
在函数的图象上，求a的值.
2. （04南京）某地举办乒乓球比赛的费用y（元）包括两部分：一部分是租用比赛场地等固定不变的费用b（元），另一部分与参加比赛的人数x（人）成正比例. 当x=20时，y=1600；当x=30时，y=2000.
（1）求y与x之间的函数关系式；
（2）如果有50名运动员参加比赛，且全部费用由运动员分摊，那么没2名运动员需要支付多少元？
3. （05海南）在我省环岛高速公路上，一辆轿车和一辆货车沿相同路线从A地到B地，所经过的路程y（千米）与时间x（小时）的函数关系如图所示，试根据图象回答下列问题：
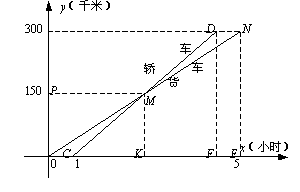（1）货车比轿车早出发__________小时，轿车追上货车时行驶了__________千米，A地到B地的距离为_________千米.
（2）轿车追上货车需要多小时？
（3）轿车比货车早到多少时间？
能力提高练习
一、跨学科综合题
1. （03恩施）在某一段电路中，保持电压不变，则 电力强度I与电阻R之间的函数关系的图象是下图中的（ ）
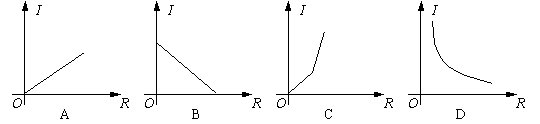
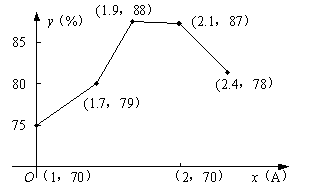
2. （03杭州）转炉炼钢产生的棕红色烟尘会污染大气，某装置可通过回收棕红色烟尘中的氧化铁从而降低污染，该装置的氧化铁回收率与其通过的电流有关，现经过试验得到下列数据：
| 通过电流强度（单位：A） | 1 | 1.7 | 1.9 | 2.1 | 2.4 |
| 氧化铁回收率（%） | 75 | 79 | 88 | 87 | 78 |
如图建立直角坐标系，用横坐标表示通过的电流强度，纵坐标表示氧化铁的回收率.
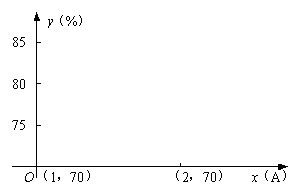（1）将试验所得数据在如图所示的直角坐标系中用点表示；（注：该
图中坐标轴的交点代表点（1，70））
（2）用线段将题（1）中所画的点从左到右顺次连接，若用此图象来模拟氧化铁回收率y关于通过电流x的函数关系，试写出该函数在1.7≤x≤2.4时的表达式；
（3）利用（2）所得函数关系，求氧化铁回收率大于85%时，该装置通过的电流应该控制的范围（精确到0.1A）.
二、实际应用题
3.
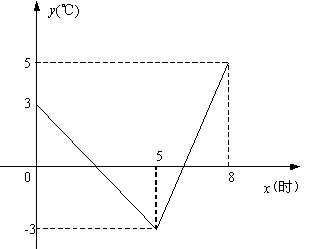（05宁夏）春、秋季节，由于冷空气的入侵，地面气温急剧下降到0℃以下的天气现象称为“霜冻”.
由霜冻导致植物生长受到影响或破坏现象称为霜冻灾害.
某种植物在气温是0℃以下持续时间超过3小时，即遭到霜冻灾害，需采取预防措施. 下图是气象台某天发布的该地区气象信息，预报了次日0时~8时气温随着时间变化情况，其中0时~5时，5时~8时的图象分别满足一次函数关系. 请你根据图中信息，针对这种植物判断次日是否需要采取防霜措施，并说明理由.
三、开放探索题：
4.
（03吉林）如图（1），在矩形ABCD中，AB=10cm，BC=8cm.
点P从A点出发，沿A→B→C→D路线运动，到D停止；点Q从D出发，沿D→C→B→A路线运动，到A停止. 若点P、点Q同时出发，点P的速度为每秒1cm，点Q的速度为每秒2cm，a秒时，点P、点Q同时改变速度，点P的速度变为每秒bcm，点Q的速度变为每秒dcm. 图（2）是点P出发x秒后△APD的面积
（cm2）与x（秒）的函数关系图象；图（3）是点Q出发x秒后△AQD的面积
（cm2）与x（秒）的函数关系图象.
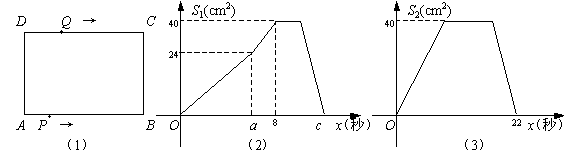
（1）参照图（2），求a、 b及图（2）中c的值；
（2）求d的值；
（3）设点P离开点A的路程为
（cm），点Q到点A还需要走的路程为
（cm），请分别写出改变速度后、与出发后的运动时间x（秒）的函数关系式，并求出P、Q相遇时x的值；
（4）当点Q出发_________秒时，点P、点Q在运动路线上的路程为为25cm.
四、创新题
5.
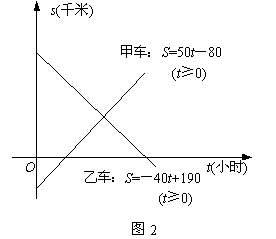
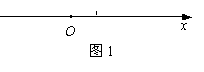甲、乙两辆汽车在一条公路上匀速行驶，为了确定汽车的位置，我们用数轴Ox表示这条公路，原点为零千米路标（如图1），并作如下约定：
①速度v>0，表示汽车向数轴正方向行驶；速度v<0，表示汽车向数轴负方向行驶；速度v=0，表示汽车静止.
②汽车位置在数轴上的坐标s>0，表示汽车位于零千米路标的右侧；汽车在数轴上的坐标s<0，表示汽车位于零千米路标的左侧；汽车在数轴上的坐标s=0，表示汽车恰好位于零千米路标处.
遵照上述约定，将这两辆汽车在公路上匀速行驶的情况，以一次函数的形式画在了同一直角坐标系中，如图2.
请解答下列问题：
（1）就这两个一次函数图象反映的两汽车在这条公路上行驶的状况填写如下的表格.
|
  | 行驶方向 | 速度的大小 （千米/时） | 出发前的位置 | ||||||||||||
（2）甲、乙两车能否相遇？如能相遇，求相遇时的时刻及在公路上的位置；如不能相遇，请说明理由.
参考答案
基础达标验收卷
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 答案 | B | D | D | D | A | A | A | C | C |
二、填空题：
| 题号 | 1 | 2 | 3 | 4 |
| 答案 |
|
|
|
|
(0≤t≤2)
三、解答题：
1. 解：（1）
；（2）
.
2. 解：（1）
；（2）每名运动员需支付56元.
3. 解：（1）1，150，300.
（2）根据图象提供的信息，可知点M为ON的中点，MK∥NE，
∴
. ∴
，即轿车追上货车需1.5小时.
（3）根据图象提供的信息，可知M为CD的中点，且MK∥DF，
∴K是CF的中点. ∴CF=3. ∴
.
∴
，即轿车比货车早到1小时.
能力提高练习
1. D.
2. 解：（1）如下图.
（2）如上图连结，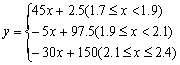
（3）当
时，由
，得
；
当
时，由
，得
；
又当
时，恒有
.
综上所述可知：满足需要时该装置的电流应控制在1.8A至2.2A之间.
3. 解：设0时~5时的一次函数解析式为
，将点
，
分别代入，得
，
. ∴
.
设5时~8时的一次函数解析式为
，将点，
分别代入，得
，
. ∴
.
当、分别为0时，
，
，而
，
∴应采取防霜冻措施.
4. 解：（1）观察图2得
S△APD=
.
∴
（秒），
（厘米/秒）.
（2）依题意
. 解得
（厘米/秒）.
（3）
，
.
依题意
.
∴
（秒）.
（4）1，19.
5. 解：（1）
|
| 行驶方向 | 速度的大小 （千米/时） | 出发前的位置 | ||||||||||||
| 甲 车 | x轴负方向（向左） | 40 | 零千米路标右侧190千米处 | ||||||||||||
| 乙 车 | x轴正方向（向右） | 50 | 零千米路标左侧80千米处 |
（2）甲乙两车能相遇.
设经过t小时两车相遇，由
得
所以经过3小时两车相遇，相遇在零千米路标右侧70千米处