中考复习专题之探索题

一、中考透视

探索性试题是近年来中考数学试题的一种新题型，也是热点题型，更是中考题多样化和时代发展要求的产物．一些省市连年考这种题型，而且在质量上也逐渐上一个新台阶，因此，在数学总复习时，必须重视这种题型．

二、特征

探索性试题往往没有明确的条件和结论，没有固定的形式和方法，要求学生通过观察、分析、比较、概括得出结论，其覆盖面广，综合性强，能力要求高．

三、解题策略：

解探索性试题需要灵活运用基础知识，大胆推理、联想、创新，恰当选用数形结合思想、转化思想和分类讨论等数学思想，多角度、多侧面、多层次思考问题，并考虑问题存在的各种可能性，从而揭示事物的整体性和一般性．

四、题型：条件探索型、结论探索型和存在性探索型．

五、例题选讲：

（一）条件探索型

例1 （青海实验区04）已知二次函数y＝0.5x²＋bx＋c的图像经过点A（c,－2），．

求证：这个二次函数图像的对称轴是x＝3．

题目中的矩形框部分是一段被墨水染污了无法辩认的文字．

（1）根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程，并画出图像；若不能，请说明理由．

（2）请你根据已有的信息，在原题中的矩形框中，填加一个适当的条件，把原题补充完整．

分析：（1）易求解析式为y=0.5x²－3x+2．

（2）以下其中的任何一种情况均可.①过抛物线的任意一点的坐标 ②顶点坐标为（3，-） ③与x轴的交点坐标（3＋，0）或（3-，0）④与y轴的交点坐标（0，2）⑤b＝-3或c=2.

评析：这类试题的特征是结论已确定，但条件未知或条件不足.解题时需要执果索因，即应把结论与题设均视为已知，然后分析探求结论成立的充分条件.通常答案不唯一.

（二）结论探索型

例2：（烟台03）如图1，AB是⊙O的直径，AC是弦，直线CD切⊙O于点C，AD⊥CD，垂足为D.

（1）求证：AC²＝AB·AD；

（2）若将直线CD向上平移，交⊙O于点C₁、C₂两点，其它条件不变，可得到图2所示的图形，试探索AC₁、AC₂、AB、AD之间的关系，并说明理由．

　　　　　　　　　　　　　

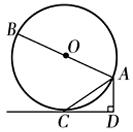
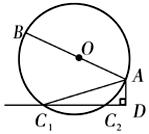
图1　　　　　　　　　 　　　　　　　　　　　　　图2

分析：（1）连结BC，可证△ACD∽△ABC．（2）关系：AC₁·AC₂＝AB·AD，可证△ADC₂∽△AC₁B．

评析：这类题的特征是给定条件，但结论不确定，其解题一般思路为：已知条件――演绎推理——推出结论．若是遇到与自然数有关的问题，则可采用归纳――猜想――证明的思维方法，去探求结论．

（三）存在性探索型

例3　已知抛物线y＝（1－m）x²＋4x－3开口向下，与x轴交于A（x₁，0）和B（x₂，0）两点，其中x₁＜x₂．

（1）求m的取值范围；

（2）若两根的平方和为10，求抛物线的解析式，并在给出直角坐标系中画出这条抛物线；

（3）设这条抛物线的顶点为C，延长CA交y轴于点D.在y轴上是否存在点P，使以P、O、B为顶点的三角形与△BCD相似？若存在，求出P点的坐标；若不存在，请说明理由．

分析：(1)易求1＜m＜；(2)易求解析式为y=-x²+4x-3；

(3)假设Rt△POB与Rt△BCD相似，则＝或＝．解得PO＝或PO＝6．符合题意.∴点P的坐标为(0,6)、(0,-6) 、(0,1.5)、(0,-1.5)．

例4　如图，梯形OABC中，O为直角坐标系的原点，A、B、C的坐标分别为（14，0）、（14，3）、（4、3）．

点P、Q同时从原点出发，分别作匀速运动。其中点P沿OA向终点A运动，速度为每秒1个单位；点Q沿OC、CB向终点B运动。当这两点中有一点到达自己的终点时，另一点也停止运动．

（1）设从出发起运动了x秒，如果点Q的速度为每秒2个单位，试分别写出这时点Q在OC上或在CB上时的坐标（用含x的代数式表示，不要求写出x的取值范围）：

（2）设从出发起运动了x秒，如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半．

①试用含x的代数式表示这时点Q所经过的路程和它的速度；

②试问：当点Q在OC上时，直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分？如有可能，求出相应的x的值和P、Q的坐标；如不能，请说明理由．

　　　　　　　　 

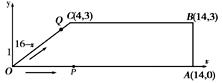
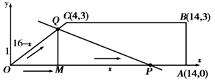
图3　　　　　　　　　　　　　　　　　　　　　　　图4

分析：（1）当点Q在OC上时，坐标为（x，x），当点Q在CB上，坐标为（2x-1，3）.

（2）①点Q所经过的路程为16-x，速度为.②当Q在OC上时，作QM⊥OA，垂足为M，则QM＝（16-x）×，∴S_△OPQ＝×（16-x）•x＝×（16-x）.令x（16－x）=18，解之，得x₁=10，x₂=6.∵当x₁=10时，16-x=6,这时点Q不在OC上，故舍去，当x₂=6，16-x=10，这时点Q不在OC上，故舍去. ∴当Q点在OC上时，PQ不可能同时把梯形OABC的面积也分成相等的两部分.

评析：这例题的特征是探索命题的结论或结论的某些方面是否存在，解题思路是：假设存在——演绎推理——得出结论，若结论合理，则存在；若结论不合理，产生矛盾，则不存在．

六、其它类型题介绍

1、（数学建模型）如图5所示，在直角三角形ABC中，∠B=90º，AB=a，BC=b（a﹥b），延长BA、BC，使AE=CD=c，直线CA、DE交于点F．

　　　　 　　　　　

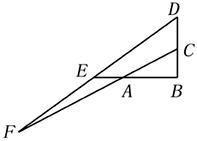
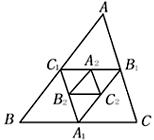
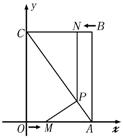
　　　　　图5　　　　　　　　　　　　　　图6　　　　　　　　　　　　　　图7

又锐角三角函数有如下性质：锐角的正弦、正切值随锐角的增大而增大；锐角的余弦值随锐角的增大而减小，请运用该性质，并根据以上所提供的几何模型证明你提炼的不等式．

2、（几何变换型）如图6所示，ΔABC的周长为a，ΔABC的三条中位线组成ΔA₁B₁C₁,ΔA₁B₁C₁的三条中位线组成ΔA₂B₂C₂，……如此进行下去得ΔA_nB_nC_n,,则

(1)ΔA₁B₁C的周长为_______,(2)ΔA₂B₂C₂的周长为_______,(3)ΔA_nB_nC_n的周长为________.

3、　　　（数形结合型）（苏州04）如图7所示，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0）、（3、4），动点M、N分别从O、B同时出发，以每秒1个单位的速度运动，其中，点M沿OA向终点A运动，点N沿BC向终点C运动．过点N作NP⊥BC，交AC于点P，连结MP，已知动点运动了x秒．

（1）　　点的坐标为（________,________）;(用含x的代数式表示)

（2）　　求ΔMPA面积的最大值，并求此时x的值；

请你探索：当x为何值时，ΔMPA是一个等腰三角形？你发现了几种情况？写出你的研究成果．

4、（阅读启示型）（绍兴04）已知一元二次方程ax²-bx+c=0的两个根满足x₁-x₂=,且a,b,c分别是ΔABC的∠A，∠B，∠C的对边，若a=c，求∠B的度数．

小敏解得此题的正确答案“∠B=120º后，思考以下问题，请你帮助解答．

（1）若在原题中，将方程改为ax²-bx=c=0,要得到∠B=120º，而条件“a=c不变，那么应对条件中的x₁-x₂的值应改为多少（不必说明理由）？

（2）  原题中，将方程改为ax²-bx+c=0(n为正整数，n≥2)，要得到∠B=120º，而条件“a=c”不变，那么条件中的x₁-x₂的值应改为多少（不必说明理由）？

5、（决策型）（河北04）光华农机租凭公司共有50台联合收割机，其中甲型20台，乙型30台，现将这些50台联合收割机派往A、B两地区收割小麦，其中共中央总书记0台派往A地区，20台派往B地区．

两地区与该农机租凭公司商定的每天的租凭价格见下表：

	每台甲型收割机的租金	每台乙型收割机的租金
A地区	1800元	1600元
B地区	1600元	1200元

（1）  设派往A地区x 台乙型联合收割机，租凭公司这些50台联合收割机一天获得的租金为y（元），求x与y间的函数关系式，并写出x的取值范围：

（2）  若使农机租凭公司这些50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来；

参考答案

1.＜　　2.（1）a （2）a （3）1/2ⁿa　 3.(1)(3-x，x)（2）x=时S的最大值为.（3）分三种情况x=1，或x=或x=.　4.（1）∣x₁-x₂∣=（2）∣x₁-x₂∣= 5.（1）y=200x+74000，x的取值范围是：10≤x≤30（x是正整数）.（2）有三种不同分配方案，即x取28,29,30这三个值.（3）当x=30时，y取最大值.