二次函数
1、(2005年安徽)一列火车自A城驶往B城,沿途有n 个车站(包括起点站A和终点站B),该列火车挂有一节邮政车厢,运行时需要在每个车站停靠,每停靠一站不仅要卸下已经通过的各车站发给该站的邮包一个,还要装上该站发往下面行程中每个车站的邮包一个.
例如,当列车停靠在第x 个车站时,邮政车厢上需要卸下已经通过的(x-1)个车站发给该站的邮包共(x-1)个,还要装上下面行程中要停靠的(n-x)个车站的邮包共(n-x)个.
(1)根据题意,完成下表:
| 车站序号 | 在第x车站启程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | |
| 5 | |
| … | …… |
| n |
(2)根据上表,写出列车在第x车站启程时,邮政车厢上共有邮包的个数y(用x、n表示).
(3)当n=18时,列车在第几个车站启程时邮政车厢上邮包的个数最多?
(1)
| 车站序号 | 在第x车站启程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | 3(n-3)-3+(n-4)=4(n-4) |
| 5 | 4(n-4)-4+(n-5)=5(n-5) |
| … | …… |
| n | 0 |
(2)y=x(n-x);(3)当n=18时,y=x(18-x)=-x2+18x=-(x-9)2+81,当x=9时,y 取得最大值.所以列车在第9个车站启程时,邮政车厢上邮包的个数最多.
2、(2005年北京)已知:在平面直角坐标系xOy中,一次函数![]() 的图象与x轴交于点A,抛物线
的图象与x轴交于点A,抛物线![]() 经过O、A两点。
经过O、A两点。
(1)试用含a的代数式表示b;
(2)设抛物线的顶点为D,以D为圆心,DA为半径的圆被x轴分为劣弧和优弧两部分。若将劣弧沿x轴翻折,翻折后的劣弧落在⊙D内,它所在的圆恰与OD相切,求⊙D半径的长及抛物线的解析式;
(3)设点B是满足(2)中条件的优弧上的一个动点,抛物线在x轴上方的部分上是否存在这样的点P,使得![]() ?若存在,求出点P的坐标;若不存在,请说明理由。
?若存在,求出点P的坐标;若不存在,请说明理由。
(1)解法一:∵一次函数![]() 的图象与x轴交于点A
的图象与x轴交于点A
∴点A的坐标为(4,0) ∵抛物线![]() 经过O、A两点
经过O、A两点
![]()
![]()
解法二:∵一次函数![]() 的图象与x轴交于点A
的图象与x轴交于点A
∴点A的坐标为(4,0)
∵抛物线![]() 经过O、A两点
经过O、A两点
∴抛物线的对称轴为直线![]()
![]()
![]() (2)解:由抛物线的对称性可知,DO=DA ∴点O在⊙D上,且∠DOA=∠DAO 又由(1)知抛物线的解析式为
(2)解:由抛物线的对称性可知,DO=DA ∴点O在⊙D上,且∠DOA=∠DAO 又由(1)知抛物线的解析式为![]() ∴点D的坐标为(
∴点D的坐标为(![]() )
)
①当![]() 时,
时,
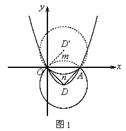
如图1,设⊙D被x轴分得的劣弧为![]() ,它沿x轴翻折后所得劣弧为
,它沿x轴翻折后所得劣弧为![]() ,显然
,显然![]() 所在的圆与⊙D关于x轴对称,设它的圆心为D' ∴点D'与点D也关于x轴对称 ∵点O在⊙D'上,且⊙D与⊙D'相切 ∴点O为切点 ∴D'O⊥OD ∴∠DOA=∠D'OA=45° ∴△ADO为等腰直角三角形
所在的圆与⊙D关于x轴对称,设它的圆心为D' ∴点D'与点D也关于x轴对称 ∵点O在⊙D'上,且⊙D与⊙D'相切 ∴点O为切点 ∴D'O⊥OD ∴∠DOA=∠D'OA=45° ∴△ADO为等腰直角三角形
![]() ∴点D的纵坐标为
∴点D的纵坐标为![]()
![]()
∴抛物线的解析式为![]() ②当
②当![]() 时, 同理可得:
时, 同理可得:![]()
抛物线的解析式为![]() 综上,⊙D半径的长为
综上,⊙D半径的长为![]() ,抛物线的解析式为
,抛物线的解析式为![]() 或
或![]()
(3)解答:抛物线在x轴上方的部分上存在点P,使得![]()
设点P的坐标为(x,y),且y>0
①当点P在抛物线![]() 上时(如图2)
上时(如图2)
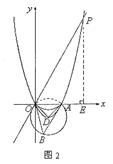
∵点B是⊙D的优弧上的一点 ![]()
![]() 过点P作PE⊥x轴于点E
过点P作PE⊥x轴于点E 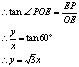
由![]() 解得:
解得:![]() (舍去)
(舍去)
∴点P的坐标为![]()
②当点P在抛物线![]() 上时(如图3)
上时(如图3)
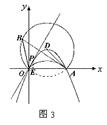
同理可得,![]()
由![]() 解得:
解得:![]() (舍去) ∴点P的坐标为
(舍去) ∴点P的坐标为![]()
综上,存在满足条件的点P,点P的坐标为 ![]() 或
或![]()
3、(长沙市 2005)已知抛物线![]() 经过点A(
经过点A(![]() ,0)、B(m,0)(m>0),且与y轴交于点C.
,0)、B(m,0)(m>0),且与y轴交于点C.
⑴求a、b的值(用含m的式子表示);
⑵如图所示,⊙M过A、B、C三点,求阴影部分扇形的面积S(用含m的式子表示);⑶在x轴上方,若抛物线上存在点P,使得以A、B、P为顶点的三角形与![]() 相似,求m的值.
相似,求m的值.

⑴依题意得有![]() ,解得
,解得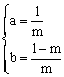
∴抛物线的解析式为:![]()
⑵∵![]() 时,
时,![]() ,∴C(0,
,∴C(0,![]() )
)
∵![]() ,∴
,∴![]() ,∴
,∴![]()
又∵![]() ,∴
,∴![]()
⑶如图,由抛物线的对称性可知,若抛物线上存在点P, 使得以A、B、P为顶点的三角形与△ABC相似,则P关于对称轴的对称点P’也符合题惫,即P、P’对应的m值相同.下面以点P在对称轴右侧进行分析:
情形一:如图,ΔABC∽△APB
则![]() ,
,![]()
过点P作![]() 垂足为D,连PA、PB.在Rt△PDA中,∵
垂足为D,连PA、PB.在Rt△PDA中,∵![]() ,∴PD=AD,∴可令P(x,x+1)
,∴PD=AD,∴可令P(x,x+1)
若点P在抛物线上,
则有![]()
即![]() ,解得
,解得![]() ,
,![]()
∴![]() (2m,2m+1),
(2m,2m+1),![]() (-1,0).显然
(-1,0).显然![]() 不合题意舍去.
不合题意舍去.
此时![]()
又由![]() ,得
,得![]()
由①、②有![]()
整理得:![]() ,解得:
,解得:![]() .
.
4、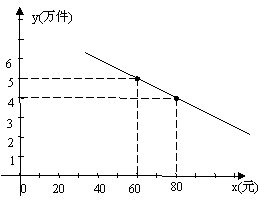 (长沙市 2005)某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
(长沙市 2005)某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
⑴求y关于x的函数关系式;
⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑶若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
解:⑴设![]() ,它过点(60,5),(80,4)
,它过点(60,5),(80,4)
∴![]() 解得
解得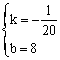 ∴
∴![]() ⑵
⑵![]()
∴当![]() 元时,最大年获得为60万元.…(6分)
元时,最大年获得为60万元.…(6分)
⑶令![]() ,得
,得![]() ,整理得:
,整理得: ![]() 解得:
解得:![]() ,
,![]() 由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
5、(2005年常德)y=(x-1)2+2的对称轴是直线 ( B )
A.x=-1 B.x=1 C.y=-1 D.y=1
6、(2005年常德)请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式 y=(x-2)2+3等 。
7、(2005年常德)某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益.通过测算:今年开关的年产量y(万只)与投入的改造经费x(万元)之间满足![]() 与
与![]() 成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
成反比例,且当改造经费投入1万元时,今年的年产量是2万只.
(1) 求年产量y(万只)与改造经费x(万元)之间的函数解析式.(不要求写出x的取值范围)
(2) 已知每生产1万只开关所需要的材料费是8万元.除材料费外,今年在生产中,全年还需支付出2万元的固定费用.
① 求平均每只开关所需的生产费用为多少元.(用含y的代数式表示)
(生产费用=固定费用+材料费)
② 如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和,那么今年生产的开关正好销完.问今年需投入多少改造经费,才能使今年的销售利润为9.5万元?
(销售利润=销售收入-生产费用-改造费用)
(1)10(2)55(3)略(4)经观察所描各点,它们在二次函数的图象上。
设:此函数的解析式为![]() 由题意得:
由题意得:
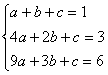 解得:
解得:![]()
所以此函数的解析式为![]()
8、(2005常州市)已知抛物线![]() 的部分图象如图,则抛物线的对称轴为直线x= 3
,满足y<0的x的取值范围是
1<x<5
,将抛物线
的部分图象如图,则抛物线的对称轴为直线x= 3
,满足y<0的x的取值范围是
1<x<5
,将抛物线![]() 向 上
平移
4 个单位,则得到抛物线
向 上
平移
4 个单位,则得到抛物线![]() .
.
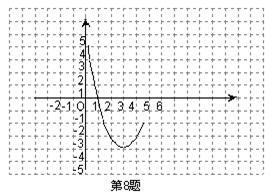
9、(枣 庄 市2005)已知抛物线![]() 的图象的一部分如图所示,抛物线的顶点在第一象限,
的图象的一部分如图所示,抛物线的顶点在第一象限,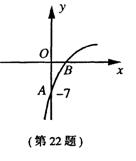 且经过点A(0,-7)和点B.
且经过点A(0,-7)和点B.
(1)求a的取值范围;
(2)若OA=2OB,求抛物线的解析式.
解:(1)由图可知,b=-7. 故抛物线为![]() 又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点.
又抛物线的顶点在第一象限,开口向下,所以抛物线与x轴有两个不同的交点.
∴ ![]() 解之,得
解之,得 ![]() . 即a的取值范围是
. 即a的取值范围是![]() .
(2)设B(x1,o),由OA=20B,得7=2x1,即
.
(2)设B(x1,o),由OA=20B,得7=2x1,即![]() .
由于
.
由于![]() ,方程(1-a)x2+8x-7=o的一个根,∴
,方程(1-a)x2+8x-7=o的一个根,∴![]() ∴
∴![]() . 故所求所抛物线解析式为
. 故所求所抛物线解析式为![]() .
.
10、(枣 庄 市2005)已知抛物线y=ax2+bx+c经过点A(-2,7),B(6,7),C(3,-8),则该抛物线上纵坐标为-8的另一点的坐标是__(1,-8) _______·
11、(南京市2005)在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子。镜子的长与宽的比是2:1。已知镜面玻璃的价格是每平方米120元,边框的价格是每米20元,另外制作这面镜子还需加工费45元。设制作这面镜子的总费用是y元,镜子的宽度是x米。
(1) 求y与x之间的关系式。
(2) 如果制作这面镜子共花了195元,求这面镜子的长和宽。
(1) y=240x2+180x+45 (2)长1m 宽0.5m
12、(丰台区2005)已知二次函数![]() 的图象如图所示,下列结论:
的图象如图所示,下列结论:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (4)
(4)![]() 。其中正确的结论有:B
。其中正确的结论有:B
A. 4个 B. 3个 C. 2个 D. 1个
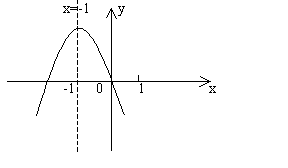
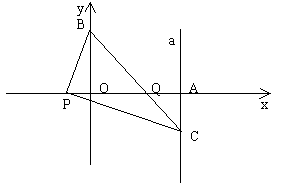
13、(丰台区2005)如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)![]() ,连结BP,过P点作
,连结BP,过P点作![]() 交过点A的直线a于点C(2,y)
交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标。
解:(1)![]()
![]()
![]() A(2,0),C(2,y)在直线a上
A(2,0),C(2,y)在直线a上 ![]()
![]()
![]() ,
,![]() ,
, ![]()
![]() (2)
(2)![]() ,
,![]() 的最大整数值为
的最大整数值为![]() 当
当![]() 时,
时,![]() ,
,![]()
![]() 设Q点坐标为
设Q点坐标为![]() ,则
,则![]()
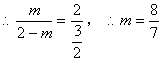
![]() 点坐标为
点坐标为![]()
14、(2005年北京市海淀)已知抛物线![]() .
.
(1) 求证此抛物线与x轴有两个不同的交点;
(2)
若m是整数,抛物线![]() 与x轴交于整数点,求m的值;
与x轴交于整数点,求m的值;
(3) 在(2)的条件下,设抛物线的顶点为A,抛物线与x轴的两个交点中右侧交点为B. 若m为坐标轴上一点,且MA=MB,求点M的坐标.
解:(1)证明:令![]() ,则
,则![]() .因为
.因为![]() =
=![]() ,所以此抛物线与x轴有两个不同的交点. (2)因为关于x的方程
,所以此抛物线与x轴有两个不同的交点. (2)因为关于x的方程![]() 的根为
的根为![]() ,由m为整数,当
,由m为整数,当![]() 为完全平方数时,此抛物线与x轴才有可能交于整数点.设
为完全平方数时,此抛物线与x轴才有可能交于整数点.设![]() (其中n为整数),则
(其中n为整数),则![]() 因为
因为![]() 与
与![]() 的奇偶性相同, 所以
的奇偶性相同, 所以![]() 或
或![]() 解得
解得 ![]() . 经过检验,当
. 经过检验,当![]() 时,方程
时,方程![]() 有整数根. 所以
有整数根. 所以![]() . (3)当m=2时,此二次函数解析式为
. (3)当m=2时,此二次函数解析式为
![]() ,则顶点坐标为
,则顶点坐标为![]() . 抛物线与x轴的交点为
. 抛物线与x轴的交点为![]() 、
、![]() .
设抛物线的对称轴与x轴交于点
.
设抛物线的对称轴与x轴交于点![]() ,则
,则![]() . 在直角三角形
. 在直角三角形![]() 中,由勾股定理,得
中,由勾股定理,得![]() . 由抛物线的对称性可得,
. 由抛物线的对称性可得,![]() . 又
. 又![]() ,即
,即![]() .所以△ABO为等腰直角三角形. 则
.所以△ABO为等腰直角三角形. 则![]() . 所以
. 所以![]() 为所求的点. 若满足条件的点
为所求的点. 若满足条件的点![]() 在y轴上时,设
在y轴上时,设![]() 坐标为
坐标为![]() , 过A作AN⊥y轴于N,连结
, 过A作AN⊥y轴于N,连结![]() 、
、![]() ,则
,则![]() .由勾股定理,有
.由勾股定理,有![]() ;
;![]() , 即
, 即![]() . 解得y=1. 所以
. 解得y=1. 所以![]() 为所求的点. 综上所述,满足条件的M点的坐标为(1,0)或(0,1).
为所求的点. 综上所述,满足条件的M点的坐标为(1,0)或(0,1).
15、 (兰州市2005)一条抛物线的对称轴是x=1且与x轴有惟一的公共点,并且开口方向向下,则这条抛物线的解析式是_y=-x2+2x-1__(任写一个)
16、(兰州市2005)已知二次函数y=ax2-4a图像的顶点坐标为(0,4)矩形ABCD在抛物线与x轴围成的图形内,顶点B、C在x轴上,顶点A、D在抛物线上,且A在D点的右侧,
(1)求二次函数的解析式
(2)设点A的坐标为(xy)试求矩形ABCD的周长L与自变量x的函数关系
(3)周长为10的矩形ABCD是否存在?若存在,请求出顶点A的坐标;若不存在,请说明理由。
解:(1)由题意得-4a=4 ∴a=-1∴二次函数的解析式为y=-x2+4
⑵ 设点A(xy)∵点A在抛物线y=-x2+4上∴y=-x2+4则AD=2x,AB=-x2+4
∴L=2(AD+AB)=2(2x-x2+4)=-2x2+4x+80<x<2 ⑶ 当L=10时 -2x2+4x+8=10x2-2x+1=0 x1=x2=1∴当x=1时,y=-12+4=3∴存在周长为10的矩形ABCD,且点A的坐标为(1,3)
17、(2005马尾区)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
(1)设每千克应涨价x元,则(10+x)(500-20x)=6000 解得x=5或x=10,为了使顾客得到实惠,所以x=5.(2)设涨价x元时总利润为y, 则y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125 当x=7.5时,y取得最大值,最大值为6125.
18、(2005马尾区)已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.
解:(1)由已知条件,得:n2-1=0
解这个方程,得: n1=1 ,n2=-1;
当n=1时,得y=x2+x,此抛物线的顶点不在第四象限;
当n=-1时,得y=x2-3x,此抛物线的顶点在第四象限;
∴所求的函数关系式为y=x2-3x
(2)由y=x2-3x,令y=0,得x2-3x=0,解得x1=0 ,x2=3;
∴抛物线与x 轴的另一个交点为(3,0)
∴它的顶点为(![]() ),对称轴为直线x=
),对称轴为直线x=![]()
①∵BC=1,由抛物线和矩形的对称性易知OB=![]()
∴B(1,0)
∴点A的横坐标x=1,又点A在抛物线y=x2-3x上,
∴点A的纵坐标y=12-3×1=-2。
∴AB=y =2
∴矩形ABCD的周长为:2(AB+BC)=6
②∵点A在抛物线y=x2-3x上,可以设A点的坐标为(x,x2-3x),
∴B点的坐标为 (x,0)。(0<x<![]()
∴BC=3-2x,A在x 轴的下方,
∴x2-3x<0
∴AB= x2-3x =3x-x2
∴矩形ABCD的周长P=2〔(3x-x2)+(3—2x)〕=-2(x-![]() )2+
)2+![]()
∵a=-2<0
∴当x=![]() 时, 矩形ABCD的周长P最大值是
时, 矩形ABCD的周长P最大值是![]() 。
。
19、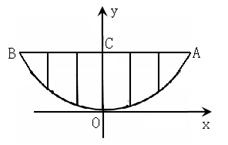 (丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(1) 以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,求出抛物线y=ax2的解析式;
(2)计算一段栅栏所需立柱的总长度.(精确到0.1米)
解:(1) 由已知:OC=0.6,AC=0.6, 得点A的坐标为(0.6,0.6),
代入y=ax2,得a=![]() , ∴抛物线的解析式为y=
, ∴抛物线的解析式为y=![]() x2.
x2.
(2)点D1,D2的横坐标分别为0.2,0.4, 代入y=![]() x2,得点D1,D2的纵坐标分别为: y1=
x2,得点D1,D2的纵坐标分别为: y1=![]() ×0.22≈0.07,y2=
×0.22≈0.07,y2=![]() ×0.42≈0.27, ∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为: 2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
×0.42≈0.27, ∴立柱C1D1=0.6-0.07=0.53,C2D2=0.6-0.27=0.33,
由于抛物线关于y轴对称,栅栏所需立柱的总长度为: 2(C1D1+ C2D2)+OC=2(0.53+0.33)+0.6≈2.3米.
20、(2005年梅州市)东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
|
| 销售量p(件) | 500 | 490 | 480 | 470 | …… |
(1)以x作为点的横坐标,p作为纵坐标,把表中的
数据,在图8中的直角坐标系中描出相应的点,观察连结
各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入件为每件40元,试求销售
利润y(元)与卖出价格x(元/件)的函数关系式
(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
解:(1)p与x成一次函数关系。
设函数关系式为p=kx+b ,则![]()
解得:k=-10,b=1000 , ∴ p=-10x+1000
经检验可知:当x=52,p=480,当x=53,p=470时也适合这一关系式
∴所求的函数关系为p=-10x+1000
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000)
∴ y=-10x2+1400x-40000
(3)由y=-10x2+1400x-40000 可知,当![]() 时,y有最大值
时,y有最大值
∴ 卖出价格为70元时,能花得最大利润。
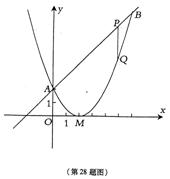 21、(2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为
21、(2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为![]() ,点P的横坐标为x,求出
,点P的横坐标为x,求出![]() 与x之间的函数关系式,并求出自变量x的取值范围;(3)在(2)的条件下,线段AB上是否P,使四边形PQMA为梯形.若存在,求出
与x之间的函数关系式,并求出自变量x的取值范围;(3)在(2)的条件下,线段AB上是否P,使四边形PQMA为梯形.若存在,求出
点P的坐标,并求出梯形的面积;若不存在,请说明理由.
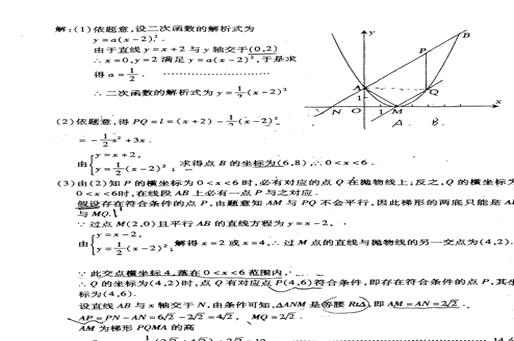
22、(2005年海安县)如图,已知抛物线![]() 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
(1)求抛物线的解析式。
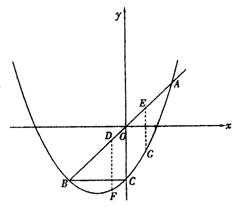 (2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
(1)∵抛物线![]() 与y轴交于点C
∴C(0,n)
与y轴交于点C
∴C(0,n)
∵BC∥x轴 ∴B点的纵坐标为n
∵B、A在y=x上,且OA=OB ∴B(n,n),A(-n,-n)
∴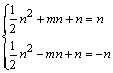 解得:n=0(舍去),n=-2;m=1
解得:n=0(舍去),n=-2;m=1
∴所求解析式为:![]()
(2)作DH⊥EG于H
∵D、E在直线y=x上 ∴∠EDH=45° ∴DH=EH
∵DE=![]() ∴DH=EH=1
∵D(x,x) ∴E(x+1,x+1)
∴DH=EH=1
∵D(x,x) ∴E(x+1,x+1)
∴F的纵坐标:![]() ,G的纵坐标:
,G的纵坐标:![]()
∴DF=![]() -(
-(![]() )=2-
)=2-![]() EG=(x+1)- [
EG=(x+1)- [![]() ]=2-
]=2-![]()
∴![]()
![]()
![]()
∴x的取值范围是-2<x<1 当x=-![]() 时,y最大值=3
时,y最大值=3![]() .
.
23、(2005年漳州)如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C。
(1)求抛物线的解析式及点A、B、C的坐标;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
 (3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。
解:(1)由抛物线的顶点是M(1,4),设解析式为![]()
又抛物线经过点N(2,3),所以![]() 解得a=-1
解得a=-1
所以所求抛物线的解析式为y=![]()
令y=0,得![]() 解得:
解得:![]()
得A(-1,0) B(3,0) ;
令x=0,得y=3,所以 C(0,3).
(2)直线y=kx+t经过C、M两点,所以![]() 即k=1,t=3
即k=1,t=3
直线解析式为y=x+3.
令y=0,得x=-3,故D(-3,0) CD=![]()
连接AN,过N做x轴的垂线,垂足为F.
设过A、N两点的直线的解析式为y=mx+n,
则![]() 解得m=1,n=1
解得m=1,n=1
所以过A、N两点的直线的解析式为y=x+1
所以DC∥AN.
在Rt△ANF中,AN=3,NF=3,所以AN=![]()
所以DC=AN。
因此四边形CDAN是平行四边形.
(3)假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u) 其中u>0,则PA是圆的半径且![]()
过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切。
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u, PM=4-u, PQ=![]()
由![]() 得方程:
得方程:![]() ,解得
,解得![]() ,
,
舍去负值u=![]() ,符合题意的u=
,符合题意的u=![]() ,
,
所以,满足题意的点P存在,其坐标为(1,![]() ).
).
24、26(2005年惠安县)如图,抛物线![]() 过点A(4,0),O为坐标原点,
过点A(4,0),O为坐标原点,
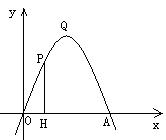 Q是抛物线的顶点. ⑴求
Q是抛物线的顶点. ⑴求![]() 的值;⑵点P是
的值;⑵点P是![]() 轴上方抛物线上的一个动点,过P作PH⊥
轴上方抛物线上的一个动点,过P作PH⊥![]() 轴,H为垂足.有一个同学说:“在
轴,H为垂足.有一个同学说:“在![]() 轴上方抛物线上的所有点中,抛物线的顶点Q与
轴上方抛物线上的所有点中,抛物线的顶点Q与![]() 轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
解:⑴∵点A(4,0)在抛物线上 ∴![]() ∴
∴![]() ∴
∴![]()
![]() ⑵设点P的坐标为
⑵设点P的坐标为![]()
![]() ∴
∴ ![]()
∴折线P-H-O的长度![]()
![]()
![]()
![]()
![]() ∴当
∴当![]() 时,折线P-H-O的长度最长为
时,折线P-H-O的长度最长为![]() ∵点Q的横坐标为2∴这个同学的说法不正确。
∵点Q的横坐标为2∴这个同学的说法不正确。
25、(2005年台州)如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
(1)设矩形的一边为![]() (m),面积为
(m),面积为![]() (m2),求
(m2),求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?
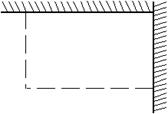 |
解:(1) 由已知,矩形的另一边长为![]()
![]()
则![]() =
= ![]()
=![]()
自变量![]() 的取值范围是0<
的取值范围是0<![]() <18.
<18.
(2)∵
![]() =
=![]() =
=![]()
∴ 当![]() =9时(0<9<18),苗圃的面积最大
=9时(0<9<18),苗圃的面积最大
最大面积是81 ![]()
又解: ∵ ![]() =-1<0,
=-1<0,![]() 有最大值,
有最大值,
∴ 当 ![]() =
=![]() 时(0<9<18),
时(0<9<18),
![]() (
(![]() )
)
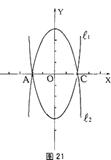
26、(玉溪市2005)如图21,已知抛物线![]() 的图象与x轴交于A、C两点。
的图象与x轴交于A、C两点。
(1)若抛物线![]() 关于x轴对称,求
关于x轴对称,求![]() 的解析式;
的解析式;
(2)若点B是抛物线![]() 上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在
上一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点记为D,求证:点D在![]() 上;
上;
(3)探索:当点B分别位于![]() 在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。
在x轴上、下两部分的图象上时,□ABCD的面积是否存在最大值或最小值?若存在,判断它是何种特殊平行四边形并求出它的面积;若不存在,请说明理由。
解:(1)设![]() 的解析式为y=
的解析式为y=![]() .
.
∵![]() 与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),
并且![]() 与
与![]() 关于x轴对称,
关于x轴对称,
∴![]() 经过点A(-2,0),C(2,0),顶点坐标是(0,4).
经过点A(-2,0),C(2,0),顶点坐标是(0,4).
∴y=![]() .
.
∴0=4a+4 得a=-1,
∴![]() 的解析式为
的解析式为![]() .
.
(2)设B(![]() )
)
∵点B在![]() 上,
上,
∴B(![]() )
)
∵四边形ABCD是平行四边形,A、C关于O对称。
∴B、D关于原点O对称,
∴D(![]() ).
).
将D(![]() )的坐标代入
)的坐标代入![]() :
:![]()
可知 左边=右边。
∴点D在![]() 上。
上。
(3)设□ABCD的面积为S,则S=2×![]() .
.
(I)当点B在x轴上方时,![]() >0,
>0,
∴![]() ,它是关于
,它是关于![]() 的正比例函数且S随
的正比例函数且S随![]() 的增大而增大,
的增大而增大,
∴S既无最大值也无最小值。
(II)当点B在x轴下方时,-4≤![]() <0.
<0.
∴![]() ,它是关于
,它是关于![]() 的正比例函数且S随
的正比例函数且S随![]() 的增大而减小,
的增大而减小,
∴当![]() =-4时,S有最大值16,但它没有最小值。
=-4时,S有最大值16,但它没有最小值。
此时B(0,-4)在y轴上,它的对称点D也在y轴上。
∴AC⊥BD.
∴□ABCD是菱形。此时![]() .
.
27、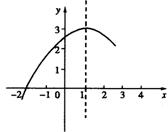 (2005年湖南省湘潭)如图;抛物线y=ax2+bx+c(a≠0)的图像与x轴的一个交点是(—2,0),顶点是(1,3)。下列说法中不正确的是( )
(2005年湖南省湘潭)如图;抛物线y=ax2+bx+c(a≠0)的图像与x轴的一个交点是(—2,0),顶点是(1,3)。下列说法中不正确的是( )
A.抛物线的对称轴是x=1
B.抛物线的开口向下
C.抛物线与x轴的另一个交点是(2,0)
D.当x=1时,y有最大值是3
28、(贵州省毕节地区2005)当你将一把扇形扇子逐渐打开时,容易发现打开部分的扇形面积随圆心角的变化而变化,那么下列函数中能正确描述这种变化的是( A )
A.正比例函数 B.反比例函数 C.一次函数(b≠0) D.二次函数
29、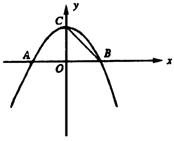 (贵州省毕节地区2005) 如图,抛物线y=―
(贵州省毕节地区2005) 如图,抛物线y=―![]() x2+(6―
x2+(6―![]() )x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
)x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
(1)求抛物线的解析式,并写出顶点坐标及对称轴方程。
(2)在抛物线上是否存在一点P使△PBC≌△OBC,
若存在,求出点P的坐标,若不存在,请说明理由。

30、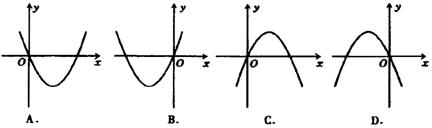 (2005年太原)在反比例函数y=
(2005年太原)在反比例函数y=![]() 中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( D )
中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( D )
31、(2005年太原) 已知二次函数y=ax2+bx+c的部分对应值如下表,求这个函数的解析式,并写出其图像的顶点坐标和对称轴。
| x | ―2 | ―1 | 0 | 1 | 2 | 3 |
| y | 0 | ―2 | ―2 | 0 | 4 | 10 |

32、(2005年太原)某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=![]() ―10;
―10;
(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;
(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理化的建议。(字数不超过50)



 ……
……