1、（2005年北京） 列方程或方程组解应用题：

　　夏季，为了节约用电，常对空调采取调高设定温度和清洗设备两种措施。某宾馆先把甲、乙两种空调的设定温度都调高1℃，结果甲种空调比乙种空调每天多节电27度；再对乙种空调清洗设备，使得乙种空调每天的总节电量是只将温度调高1℃后的节电量的1.1倍，而甲种空调节电量不变，这样两种空调每天共节电405度。求只将温度调高1℃后两种空调每天各节电多少度？

    解法一：设只将温度调高1℃后，甲种空调每天节电x度，乙种空调每天节电y度

　  依题意，得：　　解得：

　　 解法二：设只将温度调高1℃后，乙种空调每天节电x度 则甲种空调每天节电度　依题意，得：　解得： 　 

2、（长沙市 2005）某工厂第一季度生产甲、乙两种机器共480台．改进生产技术后，计划第二季度生产这两种机器共554 台，其中甲种机器产量要比第一季度增产10 % ，乙种机器产量要比第一季度增产20 % ．该厂第一季度生产甲、乙两种机器各多少台？
解：设该厂第一季度生产甲种机器x 台，乙种机器y台，依题意得：　　解得：

3、(枣 庄 市2005)某水果批发市场香蕉的价格如下表：

购买香蕉数 (千克)	不超过 20千克	20千克以上但不超过40千克	40千克以上
每千克价格	6元	5元	4元

张强两次共购买香蕉50千克(第二次多于第一次)，共付款264元，请问张强第一

次、第二次分别购买香蕉多少千克?

解：设张强第一次购买香蕉x千克，第二次购买香蕉y千克．由题意，得

　　　　  0<x<25． 　　 当0<x≤20，y≤40时，由题意，得

　　　　　　 

当0<x≤20，y>40时，由题意，得

(不合题意，舍去)．　　　　当20<x<25时，25<y<30．此时张强用去的款项为 5x+5y=5(x+y)=5×50=250<264(不合题意，舍去)　　　　 

　　综合①②③可知，张强第一次购买香蕉14千克，第二次购买香蕉36千克.

4、（南京市2005）某水果店有200个菠萝，原计划以2.6元/千克的价格出售，现在为了满足市场需要，水果店决定将所有的菠萝去皮后出售。以下是随机抽取的5个菠萝去皮前后相应的质量统计表：（单位：千克）

去皮前各菠萝的质量	1．0	1．1	1．4	1．2	1．3
去皮后各菠萝的质量	0．6	0．7	0．9	0．8	0．9

（1）　　　 计算所抽取的5个菠萝

去皮前的平均质量和去

皮后的平均质量，并估计这200个菠萝去皮前的总质量和去皮后的总质量。

（2）　　　 根据（1）的结果，要使去皮后这200个菠萝的销售总额与原计划的销售总额相同，那么去皮后的菠萝的售价应是每千克多少元？

（1）去皮前1.2千克，去皮后0.78千克。估计200个菠萝去皮前后总质量分别为240千克和156千克。（2）4元/千克。

5、(贵州省毕节地区2005)小明、小敏、小新商量要在毕业前夕给老师办公室的4道窗户剪贴窗花表达大伙的尊师之情，今年是农历鸡年，他们设计了金鸡报晓的剪纸图案。小明说：“我来出一道数学题：把剪4只金鸡的任务分配给3个人，每人至少1只，有多少种分配方法?”小敏想了想说：“设各人的任务为x、y、z，可以列出方程x+y+z=4。”小新接着说：“那么问题就成了问这个方程有几个正整数解。”现在请你说说看：这个方程正整数解的个数是(　D )

  A．6个　　　　　　 B．5个　　　　　  C．4个　　　　　　  D．3个

6、（2005年临沂市）李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水，李明家第一季度从甲、乙两供水点分别购买了10桶和6桶，共花费51元；陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶。且在乙供水点比在甲供水点多花18元钱。若只考虑价格因素，通过计算说明到哪家供水点购买这种桶装矿泉水更便宜一些？

解：设这种矿泉水在甲、乙两处每桶的价格分别为x、y元， 根据题意，得

解这个方程组，得　 ∵3.5>3，∴到甲供水点购买便宜

7、（2005广东省）李明与王云分别从A、B两地相向而行，若两人同时出发，则经过80分钟两人相遇；若李明出发60分钟后王云再出发，则经过40分钟两人相遇，问李明与王云单独走完AB全程各需多少小时？

8（2005泰州）如下图，正方形是由k个相同的矩形组成，上下各有2个水平放置的矩形，中间竖放若干个矩形，则k=　8　 .

9、(2005年河南省)如图，点O在直线AB上，OC为射线，比的3倍

少，设，的度数分别为,,那么下列求出这两个

角的度数的方程是　　　　　　　　　　　　　　　　  （ B　　 ）

 

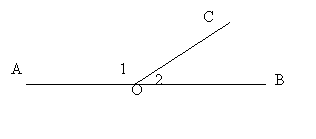
A．　　 B．　

 C．　  D．

10、(2005年潍坊)为了改善住房条件，小亮的父母考察了某小区的两套楼房，套楼房在第层楼，套楼房在第层楼，套楼房的面积比套楼房的面积大24平方米，两套楼房的房价相同，第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍．为了计算两套楼房的面积，小亮设套楼房的面积为平方米，套楼房的面积为平方米，根据以上信息列出了下列方程组．其中正确的是（　 D ）．

A．　　　　　　　　 B．

C．　　　　　　　　 D．

11、(2005年吉林)随着我国人口增长速度的减慢，小学入学儿童数量每年按逐渐减少的趋势发展。某区2003年和2004年小学入学儿童人数之比为8∶7，且2003年入学人数的2倍比2004年入学人数的3倍少1500人。某人估计2005年入学儿童数将超过2300人。请你通过计算，判断他的估计是否符合当前的变化趋势。

12、（乌鲁木齐2005）为满足市民对优质教育的需求某中学决定改变办学条件计划拆除一部分旧校舍、建造新校舍。拆除旧校舍每平米需80元，建造新校舍每平米需700元。计划在年内拆除旧校舍与建造新校舍共7200平方米，在实施中为扩大绿化面积，新建校舍只完成了计划的80％，而拆除校舍则超过了10％，结果恰好完成了原计划的拆、除的总面积。

（1）求原计划拆建面积各多少平方米？

（2）若绿化1平方米需200元，那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米？

解：设原计划拆除旧校舍x平方米，新建校舍y平方米，本世纪初题意得：

（1）

解得

（2）实际比原计划拆除与新建校舍节约资金是

（4800×80—2400×700）—〔4800×（1—10％）×80＋2400×80％×700〕

＝297600

用此资金可绿化面积是297600÷200＝1488（平方米）

13、（乌鲁木齐2005）销售某件商品可获利30元，若打9折每件商品所获利润比比原来减少了10元。则该商品的进价是＿＿＿70＿＿元。

14、（2005福州）如图2射线OC的端点O在直线AB上，∠AOC的度数比∠BOC的2倍多10°。设∠AOC和∠BOC的度数分别为x、y，则下列正确的方程组为…………（ B　）　

A、　　　　　　　  B、

C、　　　　　　　  D、

14、（2005年无锡）某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：

品名	西红柿	豆角
批发价（单位：元/㎏）	1.2	1.6
零售价（单位：元/㎏）	1.8	2.5

问：他当天卖完这些西红柿和豆角能赚多少钱？

33元.

15、(绵阳2005)已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.

由题意有

解得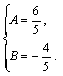：即A、B的值分别为、 .

16、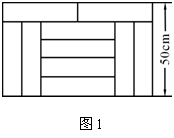(绵阳2005)如图1，宽为50 cm的矩形图案由10个全等的小长方形拼成，其中一个小长方形的面积为A

A. 400 cm²　　　　　　　　　　　　　　　　　　　　B. 500 cm²

C. 600 cm²　　　　　　　　　　　　　　　　　　　　D. 4000 cm²

17、(黄石市2005)被誉为城区风景线的杭州东路跨湖段长1857米，其各项绿化指标如表中所示，分析下表，回答下列问题：

主要树种	株数	绿化覆盖率
香樟	336	24%
柳树	188	12%
棕榈	50	3%
桂花树	50	1%
合计	832	40%

(1)　　已知杭州东路全线长4744米，在各树种行距(两树之间的水平距离)不变的情况下，请你用统计方法估计全线栽植的香樟、棕榈各多少株(结果保留整数)？

(2)　　杭州东路全线绿化工程是分期完成的，每千米的绿化投资成本一定，跨湖段是首期工程，且阳光、水份、土壤皆优于其它路段，问是否可以用跨湖段的绿化覆盖40%表示全线的绿化覆盖率？请用统计知识说明理由.

18、（遂宁市2004）足球比赛的计分规则为：胜一场得3分，平一场得1分，负一场得0分，一个队进行了14场比赛，得分不低于20分，那么该队至少胜了几场（　 A ）

A.3　　　 B.4　　　  C.5　　　　  D.6

19、（2004年无锡）西北某地区为改造沙漠，决定从2002年起进行“治沙种草”，把沙漠地变为草地，并出台了一项激励措施：在“治沙种草”的过程中，每一年新增草地面积达到10亩的农户，当年都可得到生活补贴费1500元，且每超出一亩，政府还给予每亩a元的奖励.另外，经治沙种草后的土地从下一年起，平均每亩每年可有b元的种草收入.

下表是某农户在头两年通过“治沙种草”每年获得的总收入情况：

年份	新增草地的亩数	年总收入
2002年	20亩	2600元
2003年	26亩	5060元

（注：年总收入=生活补贴费+政府奖励费+种草收入）

（1）试根据以上提供的资料确定a、b的值；

（2）从2003年起，如果该农户每年新增草地的亩数均能比前一年按相同的增长率增长，那么2005年该农户通过“治沙种草” 获得的年总收入将达到多少元？

（1）a=110，b=90.（2）1500+3630+7182=12312（元）

20、（2004年芜湖）某商场在促销期间规定：商场内所有商品按标价的80%出售，同时，当顾客在该商场内消费满一定金额后，按如下方案获得相应金额的奖券.（奖券购物不再享受优惠）

消费金额x的范围（元）	200≤x<400	400≤x<500	500≤x<700	…
获得奖券的金额（元）	30	60	100	…

根据上述促销方法，顾客在该商场购物可获得双重优惠，如果胡老师在该商场购标价450元的商品，他获得的优惠额为_____120　____元.

21、（2004年苏州）西部山区某县响应国家“退耕还林”号召，将该县一部分耕地改还林地。改还后，林地面积和耕地面积共有180km², 耕地面积是林地面积的25%。设改还后耕地面积为x km² ，林地面积为ykm²,则下列方程组中，正确的是　 （　 A　 ）

Ａ　　　  x+y=180　　　　　　 Ｂ.　　　 x+y=180　　　

　

x=25%y　　　　　　　　　　  y=25%x　　　　 

Ｃ.　　　 x+y=180　　　　 　　　　　Ｄ.　　 x+y=180

x-y=25%　　　　　　　　　　　　 y—x=25%

22、(绍兴市2004)初三（2）班的一个综合实践活动小组去A，B两个超市调查去年和今年“五一节”期间的销售情况，下图是调查后小敏与其他两位同学交流的情况.根据他们的对话，请你分别求出A，B两个超市今年“五一节” 期间的销售额.

设去年A超市销售额为x万元，B 超市销售额为y万元，

由题意得

解得

100（1+15%）=115（万元），50（1+10%）=55（万元）.

23、（安徽2004）某电视台在黄金时段的2分钟广告时间内，计划插播长度为15秒和30秒的两种广告。15秒广告每播1次收费0.6万元，30秒广告每播1次收费1万元。若要求每种广告播放不少于2次。问：

　　（1）两广告的播放的次数有几种安排方式？

（2）电视台选择哪种方式播放收益较大？

（1）设15秒广告播放x次，30秒广告播放y次，由题意得

　　15x+30y=120,

　　解得x=4,y=2或x=2,y=3。

　　（2）若x=4,y=2时，0.6×4＋1×2＝4.4万元；

　　若x=2,y=3时，0.6×2＋1×3＝4.2万元。

　　故播放15秒广告4次，30秒广告2次的方式，收益较大。

24、（河南2004）若与互为相反数，则__ _____。

25、（福州2005）如图2射线OC的端点O在直线AB上，∠AOC的度数比∠BOC的2倍多10°。设∠AOC和∠BOC的度数分别为x、y，则下列正确的方程组为…………（　B ）　

A、　　　　　　　  B、

C、　　　　　　　  D、

26、