2005年全国各地中考试题分类——03方程与不等式
一、选择题
1.(佛山市2005年)方程![]() 的解是( )
的解是( )
A.1 B.-1 C.±1 D.0
2.(扬州市2005年)关于x的方程kx2+3x-1=0有实数根, 则k的取值范围是( )
A. k≤-![]() B.k≥-
B.k≥-![]() 且k≠0 C.k≥-
且k≠0 C.k≥-![]() D.k>-
D.k>-![]() 且k≠0
且k≠0
3. (扬州市2005年)若方程![]() 有增根,则它的增根是( )
有增根,则它的增根是( )
A.0 B. 1 C. -1 D.1或-1
4. (2005年北京市)用换元法解方程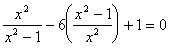 时,如果设
时,如果设![]() ,那么原方程可化为( )
,那么原方程可化为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.(2005年佛山市)已知直角三角形的两条直角边的长恰好是方程x2—5x+6=0的两根,则此直角三角形的斜边长为( ).
A.![]() B.3 C.
B.3 C.![]() D.13
D.13
|
任意圈出一竖列上相邻的三个数,请你运用方程思想来
研究,发现这三个数的和不可能是( )
A.69 B.54
C.27 D.40
7.(2005年常德市)已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,k的取值是( )
A.-3或1 B.-3 C.1 D.3
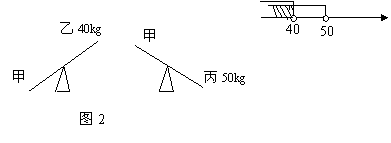
8.(2005年大连市)图2是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )
 | |||
 | |||
A B
 | |||
 | |||
C D
9.(05年深圳市)方程x2 = 2x的解是( )
A、x=2
B、x1=![]() ,x2= 0 C、x1=2,x2=0 D、x = 0
,x2= 0 C、x1=2,x2=0 D、x = 0
10.(05年深圳市)一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是( )
A、106元 B、105元 C、118元 D、108元
11.(2005年黑龙江)不等式组![]() 的解集是( )
的解集是( )
(A)x≤3 (B)l<x≤3 (C)x≥3 (D)x>1
12.(2005年黑龙江)A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,经过t小时两车相距50千米,则t的值是( )
(A)2或2.5 (B)2或10 (C)10或12.5 (D)2或12.5
二、填空题
1.(2005年黑龙江)小华的妈妈为爸爸买了一件衣服和一条裤子,共用306元.其中衣服按标价打七折,裤子按标价打八折,衣服的标价为300元,则裤子的标价为 元.
2.(佛山市2005年)不等式组![]() 的解集是
.
的解集是
.
3. (2005年北京市)不等式组![]() 的解集是____________。
的解集是____________。
4.(2005年大连市)方程![]() 的解为________.
的解为________.
5.(扬州市2005年)用换元法解方程![]() 时,若设
时,若设![]() ,则原方程变形为关于y的方程是
.
,则原方程变形为关于y的方程是
.
6. (2005年荆门市)不等式组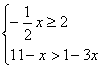 的解集为_______.
的解集为_______.
7. (2005年荆门市)在一次主题为“学会生存”的中学生社会实践活动中,春华同学为了锻炼自己,他通过了解市场行情,以每件6元的价格从批发市场购进若干件印有2008北京奥运标志的文化衫到自由市场去推销,当销售完30件之后,销售金额达到300元,余下的每件降价2元,很快推销完毕,此时销售金额达到380元,春华同学在这次活动中获得纯收入_____元.
三、解答题
1.(2005年常德市)解方程:![]() .
.
2. (2005年北京市)用配方法解方程![]() .
.
3.(北京市丰台区2005年) 用换元法解方程:![]() .
.
4.(2005年佛山市)在商品市场经常可以听到小贩的叫嚷声和顾客的讨价还价声:“10元一个的玩具赛车打八折,快来买啊!”“能不能再便宜2元?”如果小贩真的让利(便宜)2元卖了,他还能获利20%,根据下列公式求一个玩具赛车进价是多少元?(公式:利润=进价×利润率=销售价×打折数—让利数—进价)
5.(扬州市2005年) 宝应县是江苏省青少年足球训练基地,每年都举行全县中小学生足球联赛.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分.2004年的联赛中某校足球队参加了16场比赛,共得30分.已知该队只输了2场,那么这个队胜了几场?平了几场?
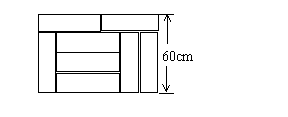
6.(北京市丰台区2005年)列方程或方程组解应用题:用8块相同的长方形地砖拼成一块矩形地面,地砖的拼放方式及相关数据如图所示,求每块地砖的长与宽.
7. (2005年北京市)列方程或方程组解应用题:夏季,为了节约用电,常对空调采取调高设定温度和清洗设备两种措施。某宾馆先把甲、乙两种空调的设定温度都调高1℃,结果甲种空调比乙种空调每天多节电27度;再对乙种空调清洗设备,使得乙种空调每天的总节电量是只将温度调高1℃后的节电量的1.1倍,而甲种空调节电量不变,这样两种空调每天共节电405度。求只将温度调高1℃后两种空调每天各节电多少度?
8.(2005年大连市)某企业的年产值在两年内从1000万元增加到1210万元,求平均每年增长的百分率.
9.(佛山市2005年)某酒店客房部有三人间、双人间客房,收费数据如下表.

为吸引游客,实行团体入住五折优惠措施.一个50人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房.若每间客房正好住满,且一天共花去住宿费1510元,则旅游团住了三人普通间和双人普通间客房各多少间?
10.(05年深圳市)某工程,甲工程队单独做40天完成,若乙工程队单独做30天后,甲、乙两工程队再合作20天完成.
(1)求乙工程队单独做需要多少天完成?
(2)将工程分两部分,甲做其中一部分用了x天,乙做另一部分用了y天,其中x、y均为正整数,且x<15,y<70,求x、y..
11.(2005年黑龙江)已知关于x的一元二次方程x2+(4m+1)x+2m-1=O.
(1)求证:不论m为任何实数,方程总有两个不相等的实数根;
(2)若方程两根为x1、x2,且满足+=-,求m的值.
12.(2005年河南省)某公司为了扩大经营,决定购进6台机器用于生产某种活塞。现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示。经过预算,本次购买机器所耗资金不能超过34万元.
| 甲 | 乙 | |
| 价格(万元/台) | 7 | 5 |
| 每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种方案?
13. (2005年荆门市)已知关于x的方程![]() 的两根是一个矩形两邻边的长.
的两根是一个矩形两邻边的长.
⑴k取何值时,方程在两个实数根;
⑵当矩形的对角线长为![]() 时,求k的值.
时,求k的值.
14. (2005年荆门市)某校初中三年级270名师生计划集体外出一日游,乘车往返,经与客运公司联系,他们有座位数不同的中巴车和大客车两种车型可供选择,每辆大客车比中巴车多15个座位,学校根据中巴车和大客车的座位数计算后得知,如果租用中巴车若干辆,师生刚好坐满全部座位;如果租用大客车,不仅少用一辆,而且师生坐完后还多30个座位.
⑴求中巴车和大客车各有多少个座位?
⑵客运公司为学校这次活动提供的报价是:租用中巴车每辆往返费用350元,租用大客车每辆往返费用400元,学校在研究租车方案时发现,同时租用两种车,其中大客车比中巴车多租一辆,所需租车费比单独租用一种车型都要便宜,按这种方案需要中巴车和大客车各多少辆?租车费比单独租用中巴车或大客车各少多少元?
参考答案
一、1.D 2.C 3.B 4. C 5.C 6.D 7.C 8.C 9.C 10.D 11.B 12.A
二、1.120 2.![]() 3.
3. ![]() 4.x=1 5.
4.x=1 5.![]() 6.-5<x≤-4
7.140
6.-5<x≤-4
7.140
三、1. 解:6-3(x+1)=x2-1,x2+3x-4=0,(x+4)(x-1)=0.x1=-4,x2=1.经检验x=1是增根,应舍去.∴原方程的解为x=-4.
2. 解:移项,得:![]() ,配方,得:
,配方,得:![]() ,
,![]() .解这个方程,得:
.解这个方程,得:![]() ,即
,即![]() .
.
3.解:设![]() ,那么
,那么![]() ,于是原方程变形为
,于是原方程变形为 ![]() .方程的两边都乘以y,约去分母,并整理,得
.方程的两边都乘以y,约去分母,并整理,得![]() .解这个方程,得
.解这个方程,得![]() ,
,![]() .当
.当![]() 时,
时,![]() ,即
,即![]() .解这个方程,得
.解这个方程,得![]() .当
.当![]() 时,
时,![]() ,即
,即![]() ,因为
,因为![]() ,所以,这个方程没有实数根.经检验,
,所以,这个方程没有实数根.经检验,![]() 都是原方程的根.∴原方程的根是
都是原方程的根.∴原方程的根是![]() .
.
4.解:设进价是![]() 元,依题意,得
元,依题意,得![]() .解得
.解得![]() (元).答:(略).
(元).答:(略).
5.解:方法一:设这个队胜了x场,平了y场,根据题意,得![]() 解之得
解之得![]() 方法二:设这个队胜了x场,则平了(14-x)场,根据题意,得3x+(14-x)=30,解之得x=8,则14-x=6.答:这个队胜了8场,平了6场.
方法二:设这个队胜了x场,则平了(14-x)场,根据题意,得3x+(14-x)=30,解之得x=8,则14-x=6.答:这个队胜了8场,平了6场.
6.解:设每块地砖的长为xcm,宽为ycm.根据题意,得![]() .解这个方程组,得
.解这个方程组,得![]() .答:每块地砖的长为45cm,宽为15cm .
.答:每块地砖的长为45cm,宽为15cm .
7. 解法一:设只将温度调高1℃后,甲种空调每天节电x度,乙种空调每天节电y度.依题意,得:![]() ,解得:
,解得:![]() .解法二:设只将温度调高1℃后,乙种空调每天节电x度,则甲种空调每天节电
.解法二:设只将温度调高1℃后,乙种空调每天节电x度,则甲种空调每天节电![]() 度.依题意,得:
度.依题意,得:![]() .解得:
.解得:![]() ,
,![]() .答:只将温度调高1℃后,甲种空调每天节电207度,乙种空调每天节电180度.
.答:只将温度调高1℃后,甲种空调每天节电207度,乙种空调每天节电180度.
8.解:设平均每年增长的百分率为x,根据题意,得1000(1+x)2=1210,![]() ,解这个方程,得x1=0.1=10%,x2=-2.1.由于增长率不能为负数,所以x=-2.1不符合题意,因此符合本题要求的x为0.1=10%.答:平均每年增长的百分率为10%.
,解这个方程,得x1=0.1=10%,x2=-2.1.由于增长率不能为负数,所以x=-2.1不符合题意,因此符合本题要求的x为0.1=10%.答:平均每年增长的百分率为10%.
9.解法一:设三人普通房和双人普通房各住了![]() 、
、![]() 间,根据题意,得
间,根据题意,得![]() 解得
解得![]() 解法二:设三人普通房和双人普通房各住了
解法二:设三人普通房和双人普通房各住了![]() 、
、![]() 人,根据题意,得
人,根据题意,得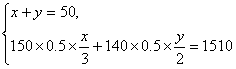 解得
解得![]() 且
且![]() (间),
(间),![]() (间).解法三:设三人普通房共住了
(间).解法三:设三人普通房共住了![]() 人,则双人普通房共住了
人,则双人普通房共住了![]() 人,根据题意,得
人,根据题意,得![]() .解得
.解得 ![]() ,且
,且![]() (间),
(间),![]() (间).答:三人间普通客房、双人间普通客房各住了8、13间.
(间).答:三人间普通客房、双人间普通客房各住了8、13间.
10.解:(1)设乙工程队单独做需要x天完成.则30×![]() +20(
+20(![]() )=1,解之得:x=100.经检验得x=100是所列方程的解,所以求乙工程队单独做需要100天完成.(2)甲做其中一部分用了x天,乙做另一部分用了y天,所以
)=1,解之得:x=100.经检验得x=100是所列方程的解,所以求乙工程队单独做需要100天完成.(2)甲做其中一部分用了x天,乙做另一部分用了y天,所以![]() ,即:y=100 -
,即:y=100 -![]() ,又x<15,y<70,所以
,又x<15,y<70,所以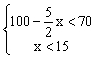 ,解之得:12<x<15,所以x=13或14,又y也为正整数,所以x=14,y=65.
,解之得:12<x<15,所以x=13或14,又y也为正整数,所以x=14,y=65.
11.解:(1)证明:△=(4m+1)2-4(2m-1)=16m2+8m+1-8m+4=16m2+5>O,∴ 不论m为任何实数,方程总有两个不相等的实数根.(2)∵ xl+x2=-(4m+1),xl·x2=2m-l,∴ +===-,解得m=-.
12.(1)设购买甲种机器x台,则购买乙种机器(6-x)台.由题意,得![]() ,
,
解这个不等式,得![]() ,即x可以取0、1、2三个值,所以,该公司按要求可以有以下三种购买方案:方案一:不购买甲种机器,购买乙种机器6台;方案二:购买甲种机器1台,购买乙种机器5台;方案三:购买甲种机器2台,购买乙种机器4台.(2)按方案一购买机器,所耗资金为30万元,新购买机器日生产量为360个;按方案二购买机器,所耗资金为1×7+5×5=32万元;,新购买机器日生产量为1×100+5×60=400个;按方案三购买机器,所耗资金为2×7+4×5=34万元;新购买机器日生产量为2×100+4×60=440个。因此,选择方案二既能达到生产能力不低于380个的要求,又比方案三节约2万元资金,故应选择方案二.
,即x可以取0、1、2三个值,所以,该公司按要求可以有以下三种购买方案:方案一:不购买甲种机器,购买乙种机器6台;方案二:购买甲种机器1台,购买乙种机器5台;方案三:购买甲种机器2台,购买乙种机器4台.(2)按方案一购买机器,所耗资金为30万元,新购买机器日生产量为360个;按方案二购买机器,所耗资金为1×7+5×5=32万元;,新购买机器日生产量为1×100+5×60=400个;按方案三购买机器,所耗资金为2×7+4×5=34万元;新购买机器日生产量为2×100+4×60=440个。因此,选择方案二既能达到生产能力不低于380个的要求,又比方案三节约2万元资金,故应选择方案二.
13.解:⑴ 要使方程有两个实数根,必须△≥0,即![]() ≥0,化简得:2k-3≥0,解之得:k≥
≥0,化简得:2k-3≥0,解之得:k≥![]() .⑵设矩形的两邻边长分别为a、b,则有
.⑵设矩形的两邻边长分别为a、b,则有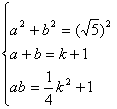 解之得:k1=2,k2=-6.由⑴可知,k=-6时,方程无实数根,所以,只能取k=2.
解之得:k1=2,k2=-6.由⑴可知,k=-6时,方程无实数根,所以,只能取k=2.
14.解:⑴设每辆中巴车有座位x个,每辆大客车有座位(x+15)个,依题意有![]() ,解之得:x1=45,x2=-90(不合题意,舍去).答:每辆中巴车有座位45个,每辆大客车有座位60个.⑵解法一:①若单独租用中巴车,租车费用为
,解之得:x1=45,x2=-90(不合题意,舍去).答:每辆中巴车有座位45个,每辆大客车有座位60个.⑵解法一:①若单独租用中巴车,租车费用为![]() ×350=2100(元);②若单独租用大客车,租车费用为(6-1)×400=2000(元);③设租用中巴车y辆,大客车(y+1)辆,则有45y+60(y+1)≥270,解得y≥2,当y=2时,y+1=3,运送人数为45×2+60×3=270合要求.这时租车费用为350×2+400×3=1900(元),故租用中巴车2辆和大客车3辆,比单独租用中巴车的租车费少200元,比单独租用大客车的租车费少100元.解法二:③设租用中巴车y辆,大客车(y+1)辆,则有350y+400(y+1)<2000,解得:
×350=2100(元);②若单独租用大客车,租车费用为(6-1)×400=2000(元);③设租用中巴车y辆,大客车(y+1)辆,则有45y+60(y+1)≥270,解得y≥2,当y=2时,y+1=3,运送人数为45×2+60×3=270合要求.这时租车费用为350×2+400×3=1900(元),故租用中巴车2辆和大客车3辆,比单独租用中巴车的租车费少200元,比单独租用大客车的租车费少100元.解法二:③设租用中巴车y辆,大客车(y+1)辆,则有350y+400(y+1)<2000,解得:![]() 。故y=1或y=2.
。故y=1或y=2.
