七、阅读型试题
例1、（2005年台州）我国古代数学家秦九韶在《算书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积。用现代式子表示即为：
……①（其中a、b、c为三角形的三边长，s为面积）。而另一个文明古国古希腊也有求三角形面积的海伦公式：
……②（其中
）。
（1） 若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积。
（2） 你能否由公式①推导出公式②？请试试。
知识点：本题考查了多项式乘法、分解因式、二次根式及其化简等有关知识。
精析：这是一道阅读理解题，它要求学生通过阅读理解“三斜求积术”的现在代公式，第（1）小题是检验学生的阅读能力及学以致用的能力，第（2）题是考查学生是创新能力。
准确答案：
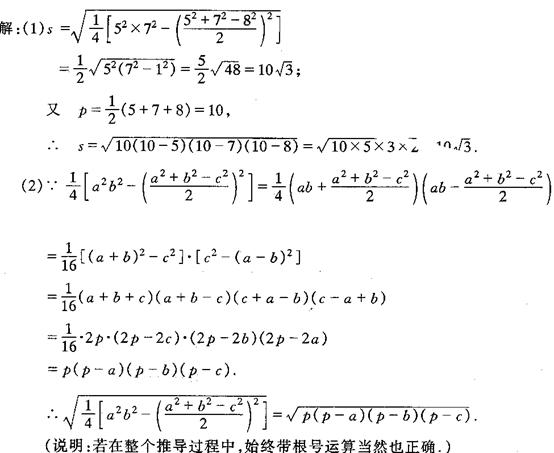
中考对该知识点的要求：近几年中考试题中，阅读理解型试题题型新颖，形式多样，知识覆盖面较大，它可以是总计课本原文，也可以是设计一个新的数学情境，让学生在阅读的基础上，理解其中的内容、方法、思想，然后把握本质，理解实质的基础上作出回答。
目标达成：
7－1－1．（2005年贵州市）阅读下面操作过程，回答后面问题：在一次数学实践探究活动中，小强过A、C两点画直线AC把平行四边形ABCD分割成两个部分（如图12（
）），小刚过AB、AC的中点画直线EF，把平行四边形ABCD也分割成两个部分（如图12（
））；
图12
（）
（）
（
）
（1）这两种分割方法中面积之间的关系为：
，
；
（2）根据这两位同学的分割方法，你认为把平行四边形分割成满足以上面积关系的直线
有
条，请在图12（）的平行四边形中画出一种；
（3）由上述实验操作过程，你发现了什么规律？
（3）经过平行四边形对称中心的任意直线，都可以把平行四边形分成满足条件的图形；
7－1－2．（2005年资阳市）阅读以下短文，然后解决下列问题：
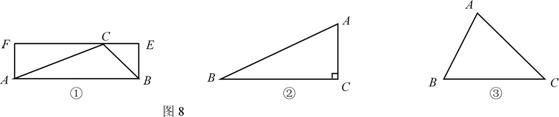
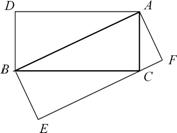
如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”. 如图8①所示，矩形ABEF即为△ABC的“友好矩形”. 显然，当△ABC是钝角三角形时，其“友好矩形”只有一个 .
(1) 仿照以上叙述，说明什么是一个三角形的“友好平行四边形”；
(2) 如图8②，若△ABC为直角三角形，且∠C=90°，在图8②中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；
(3) 若△ABC是锐角三角形，且BC>AC>AB，在图8③中画出△ABC的所有“友好矩形”，指出其中周长最小的矩形并加以证明.
7－1－3．（2005年玉林）阅读下列材料，并解决后面的问题．
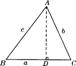在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c．过A作AD⊥BC于D(如图)，则sinB=
，sinC=
，即AD=csinB，AD=bsinC，于是csinB=bsinC，即
．
同理有
，
．
所以
………(*)
即：在一个三角形中，各边和它所对角的正弦的比相等．
(1)在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论(*)和有关定理就可以
求出其余三个未知元素c、∠B、∠C，请你按照下列步骤填空，完成求解过程：
第一步：由条件a、b、∠A
∠B；
第二步：由条件 ∠A、∠B． ∠C；
第三步：由条件．
c．
(2)一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以28．4海里／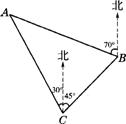
时的速度按北偏东45°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西70°的方向上(如图11)，求此时货轮距灯塔A的距离AB(结果精确到0．1．参考数据：sin40°=0．6 4 3，sin65°=0．90
6，sin70°=0．940，sin7 5°=0．9 6 6)．
7－1－4、（2005年佛山）“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB置于直角坐标系中，边OB在
轴上、边OA与函数
的图象交于点P，以P为圆心、以2OP为半径作弧交图象于点R．分别过点P和R作轴和
轴的平行线，两直线相交于点M ，连接OM得到∠MOB，则∠MOB=
∠AOB．要明白帕普斯的方法，请研究以下问题：
（1）设
、
，求直线OM对应的函数表达式（用含
的代数式表示）．
（2）分别过点P和R作轴和轴的平行线，两直线相交于点Q．请说明Q点在直线OM上，并据此证明∠MOB=∠AOB．
（3）应用上述方法得到的结论，你如何三等分一个钝角（用文字简要说明）．
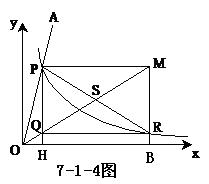
7－1－5、（2005年福州）已知：如图8，AB是⊙O的直径，P是AB上的一点（与A、B不重合），QP⊥AB，垂足为P，直线QA交⊙O于C点，过C点作⊙O的切线交直线QP于点D。则△CDQ是等腰三角形。
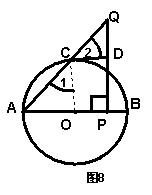对上述命题证明如下：
证明：连结OC
∵OA＝OC
∴∠A＝∠1
∵CD切O于C点
∴∠OCD＝90°
∴∠1＋∠2＝90°
∴∠A＋∠2＝90°
在RtQPA中，QPA＝90°
∴∠A＋∠Q＝90° ∴∠2＝∠Q ∴DQ＝DC
即CDQ是等腰三角形。
问题：对上述命题，当点P在BA的延长线上时，其他条件不变，如图9所示，结论“△CDQ是等腰三角形”还成立吗？若成立，误给予证明；若不成立，请说明理由。
能力提高：
7－1、（2005年内江）阅读材料，大数学家高斯在上学读书时
曾经研究过这样一个问题：
1+2+3+…+100＝？经过研究，这个问题的一般性结论是1+2+3+…+
，其中ｎ是正整数。现在我们来研究一个类似的问题：1×2+2×3+…
＝？
观察下面三个特殊的等式
将这三个等式的两边相加，可以得到1×2+2×3+3×4＝
读完这段材料，请你思考后回答：
⑴
⑵
⑶
（只需写出结果，不必写中间的过程）
7－2、（2005年陕西）阅读：我们知道，在数轴上，x＝1表示一个点，而在平面直角坐标系中，x＝1表示一条直线；我们还知道，以二元一次方程2x－y＋1＝0的所有解为坐标的点组成的图形就是一次函数y＝2x＋1的图象，它也是一条直线，如图①.
观察图①可以得出：直线＝1与直线y＝2x＋1的交点P的坐标（1，3）就是方程组
的解，所以这个方程组的解为
在直角坐标系中，x≤1表示一个平面区域，即直线x＝1以及它左侧的部分，如图②；y≤2x＋1也表示一个平面区域，即直线y＝2x＋1以及它下方的部分，如图③。
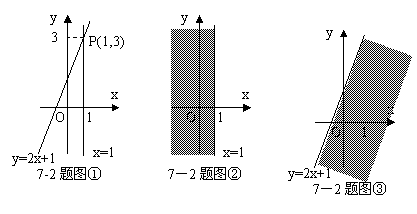
回答下列问题：
（1）
在直角坐标系（图④）中，用作图象的方法求出方程组
的解；
（2）
用阴影表示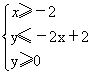
，所围成的区域。
答案：
7－1－1．（1）
，；
（2）无数，图略；
7－1－2．(1) 如果一个三角形和一个平行四边形满足条件：三角形的一边与平行四边形的一边重合，三角形这边所对的顶点在平行四边形这边的对边上，则称这样的平行四边形为三角形的“友好平行四边形”.
(2) 此时共有2个友好矩形，如图的BCAD、ABEF.
易知，矩形BCAD、ABEF的面积都等于△ABC面积的2倍，∴ △ABC的“友好矩形”的面积相等.
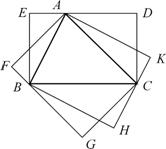
(3) 此时共有3个友好矩形，如图的BCDE、CAFG及ABHK，其中的矩形ABHK的周长最小 .
证明如下：
易知，这三个矩形的面积相等，令其为S. 设矩形BCDE、CAFG及ABHK的周长分别为L1，L2，L3，△ABC的边长BC=a，CA=b，AB=c，则
L1=
+2a，L2=
+2b，L3=
+2c .
∴ L1-
L2=(+2a)-(+2b)=2(a-b)
，
而 ab>S，a>b，
∴ L1- L2>0，即L1> L2 .
同理可得，L2> L3 .
∴ L3最小，即矩形ABHK的周长最小.
7－1－3．解：(1) , ∠A+∠B+∠C=180°，a、∠A、∠C或b、∠B、∠C，
或
(2)依题意，可求得∠ABC=65°，
∠A=40°.
BC=14．2．
AB≈21．3．
答：货轮距灯塔A的距离约为21．3海里．(9分)
7－1－4、解：（1）设直线OM的函数关系式为
．
则
∴
．
∴直线OM的函数关系式为
．
（2）∵
的坐标
满足，∴点在直线OM上．
∵四边形PQRM是矩形，∴SP=SQ=SR=SM=
PR．
∴∠SQR=∠SRQ．
∵PR=2OP，∴PS=OP=PR．∴∠POS=∠PSO．
∵∠PSQ是△SQR的一个外角，
∴∠PSQ=2∠SQR．∴∠POS=2∠SQR．
∵QR∥OB，∴∠SOB=∠SQR．
∴∠POS=2∠SOB．
∴∠SOB=∠AOB．
（3）以下方法只要回答一种即可．
方法一：利用钝角的一半是锐角，然后利用上述结论把锐角三等分的方法即可．
方法二：也可把钝角减去一个直角得一个锐角，然后利用上述结论把锐角三等分后，再将直角利用等边三角形（或其它方法）将其三等分即可．
方法三：先将此钝角的补角（锐角）三等分，再作它的余角．
7－1－5、答：结论“△CDQ是等腰三角形”还成立
证明：略
7－1、⑴343400(或
⑵
⑶
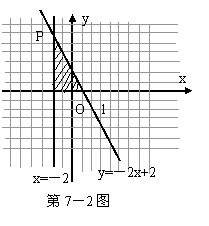7－2. 解：（1）如图所示，
在坐标系中分别作出直线x＝－2和直线y＝－2x＋2，
这两条直线的交点是P（－2，6）。
则
是方程组的解。
（3） 如阴影所示。