六安海峰学校中考模拟数学试卷

一、　  选择题（本题共40分）

下列各题都有代号为A、B、C、D的四个结论供选择，其中只有一个结论是正确的。

1、  －5的相反数等于（　　 ）

A、5　　　　　　　　　　　B、　　　　　　　　　 C、－5　　　　　　　　 D、－

2、  如图，在正方体ABCD－A₁B₁C₁D₁中，下列棱中与面CC₁D₁D垂直的棱是（　　 ）

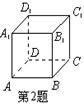A、A₁B₁B、CC₁C、BC　　　　　　　　　D、CD

3、  若分式的值为零，则x等于（　　 ）

A、0　　　　　　　　　　　B、1　　　　　　　　　　 C、　　　　　　　　　D、－1

4、  已知等腰三角形的一个底角等于30°，则这个等腰三角形的顶角等于（　　 ）

A、150°　　　　　　　 B、120°　　　　　　　C、75°　　　　　　　 D、30°

5、 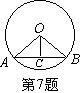 如图，已知O的半径OA长为5，弦AB长为8，C是AB的中点，

则OC的长为（　　 ）

A、3　　　　　　　　　　　B、6　　　　　　　　　　 C、9　　　　　　　　　　 D、10

6、  下列图形中既是轴对称图形又是中心对称图形的是（　　 ）

A　　　　　　　　　 　B　　　　　　　　　C　　　　　　　　　　　　D

7、  一列列车自2004年全国铁路第5次大提速后，速度提高了26千米/时，现在该列车从甲站到乙站所用的时间比原来减少了1小时，已知甲、乙两站的路程是312千米，若设列车提速前的速度是x千米，则根据题意所列方程正确的是（　　 ）

A、　　　　　　　B、

C、　　　　　　　D、

8、　　　  抛物线的对称轴是（　　 ）

A、x＝－2　　　　　B、x＝2　　　　 C、x＝－4　　　　　　D、x＝4

9、　　　  某中学新科技馆铺设地面，已有正三角形形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该学校不应该购买的地砖形状是（　　 ）

A、正方形　　　　B、正六边形　　　　 C、正八边形　　　　D、正十二边形

10、　  据《南通日报》2004年3月18日报道，在2003年度中国城市综合指标座次排名中，南通市在苏中、苏北独占鳌头，各项综合指标的名次如图：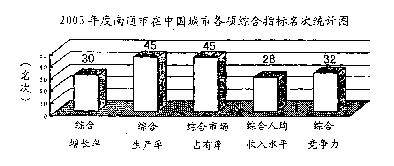

则图中五个数据的众数和平均数依次是（　　 ）

A、32，36　　　　　　 B、45，36　　　　　　C、36，45　　　　　　D、45，32

二、填空题（本题共40分）把最后结果填在题中横线上。

11、计算sin30°cot45°____________

12、点M（1，2）关于x轴对称点的坐标为____________

13、如图，是一个简单的数值运算程序

当输入x的值为－1时，则输出的数值为 ___________

14、化简的结果为　　　

15、如图，为了求出湖两岸A、B两点之间的距离，观测者

从测点A、B分别测得∠BAC＝90°，∠ABC＝30°，

又量得BC＝160 m，则A、B两点之间的距离为　　m（结果保留根号）

16、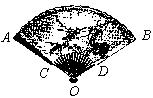换元法解方程，若设，则原方程可化为关于y的一元二次方程为　　　　　　　　　　　

17、图，一扇形纸扇完全打开后，两竹条外侧OA和OB的夹角为120°，OC长为8cm，贴纸部分的CA长为15cm，则贴纸部分的面积为　　　　cm²（结果保留π）

18、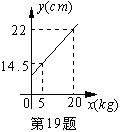请任意写一个能在实数范围内分解因式的二次三项式　　　　  （该二次三项式的字母、系数不限）

19、如图，如图，弹簧总长y（cm）与所挂物体质量x（kg）之间是一

次函数关系，则该弹簧不挂物体时的长度为　　　　　  cm

20、已知一个矩形的长为3cm， 宽为2cm， 试 估算 它的对角线长

为　　　　　cm（结果保留两个有效数字，要求误差小于0.2）

三、解答题

21、（本小题10分）

⑴在所给数轴上画出表示数－3，－1，的点。　　 ⑵计算：

22、（本小题5分）

解方程组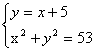

23、（本小题5分）

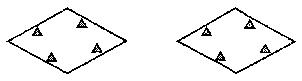
如图，菱形公园内有四个景点，请你用两种不同的方法，按下列要求设计成四个部分：⑴用直线分割；⑵每个部分内各有一个景点；⑶各部分的面积相等。（可用铅笔画，只要求画图正确，不写画法）

24、（本小题10分）

已知关于x的一元二次方程

⑴请选取一个你喜爱的m的值，使方程有两个不相等的实数根，并说明它的正确性；

⑵设x₁，x₂是⑴中所得方程的两个根，求x₁x₂＋x₁＋x₂的值。

25、（本小题10分）

小刚为书房买灯，现有两种灯可供选购，其中一种是9瓦（即0.009千瓦）的节能灯，售价49元/盏；另一种是40瓦（即0.04千瓦）的白炽灯，售价为18元/盏。假设两种灯的照明亮度一样，使用寿命都可以达到2800小时，已知小刚家所在地的电价是每千瓦0.5元。

⑴设照明时间是x小时，请用含x的代数式分别表示用一盏节能灯的费用和用一盏白炽灯的费用（注：费用＝灯的售价＋电费）

⑵小刚想在这两种灯中选购一盏

①当照明时间是多少时，使用两种灯的费用一样多；

②试用特殊值推断

照明时间在什么范围内，选用白炽灯费用低；

照明时间在什么范围内，选用节能灯费用低；

⑶小刚想在这两种灯中选购两盏

假定照明时间是3000小时，使用寿命都是2800小时，请你帮他设计费用最低的选灯方案，并说明理由。

26、（本小题10分）

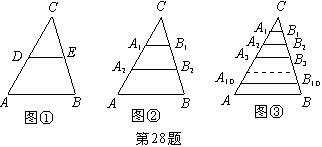
已知：△ABC中，AB＝10

⑴如图①，若点D、E分别是AC、BC边的中点，求DE的长；

⑵如图②，若点A₁、A₂把AC边三等分，过A₁、A₂作AB边的平行线，分别交BC边于点B₁、B₂，求A₁B₁＋A₂B₂的值；

⑶如图③，若点A₁、A₂、…、A₁₀把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B₁、B₂、…、B₁₀。根据你所发现的规律，直接写出A₁B₁＋A₂B₂＋…＋A₁₀B₁₀的结果。

27、（本小题10分）

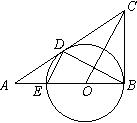
已知：如图，在△ABC中，∠ABC＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点D，连结DB、DE、OC。

⑴从图中找出一对相似三角形（不添加任何字母和辅助线），并证明你的结论；

⑵若AD＝2，AE＝1，求CD的长。

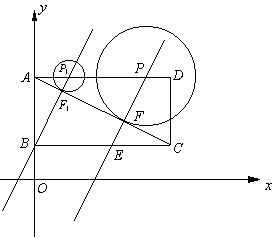
28、（本小题10分）

已知，如图，直角坐标系内的矩形ABCD，顶点A的坐标为（0，3），BC＝2AB，P为AD边上一动点（与点A、D不重合），以点P为圆心作⊙P与对角线AC相切于点F，过P、F作直线L，交BC边于点E ，当点P运动到点P₁位置时，直线L恰好经过点B，此时直线的解析式是y＝2x＋1

⑴求BC、AP₁的长；

⑵设AP＝m，梯形PECD的面积为S，求S与m之间的函数关系式，写出自变量m的取值范围；

⑶以点E为圆心作⊙E与x轴相切

①探究并猜想：⊙P和⊙E有哪几种位置关系，并求出AP相应的取值范围；

②当直线L把矩形ABCD分成两部分的面积之比值为3∶5时，则⊙P和⊙E的位置关系如何？并说明理由。