2005年苏州市初中毕业暨升学考试试卷(数学)
中考试卷
第I卷(选择题,共24分)
一. 选择题:本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 下列运算错误的是( )
A. ![]()
B. ![]()
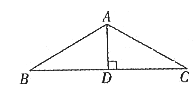
C. ![]()
D. ![]()
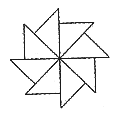
2. 下图可以看作是一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是( )
A. 90° B. 60° C. 45° D. 30°
3. 据苏州市红十字会统计,2004年苏州市无偿献血者总量为12.4万人次,已连续6年保持全省第一。12.4万这个数用科学记数法表示是()
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
4. 将直线![]() 向上平移两个单位,所得的直线是(
)
向上平移两个单位,所得的直线是(
)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
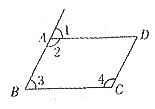
5. 如图所示,在平行四边形ABCD中,下列各式不一定正确的是( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
6. 初二(1)班有48位学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中,“想去苏州乐园的学生数”的扇形圆心角是60°,则下列说法正确的是()
A. 想去苏州乐园的学生占全班学生的60%
B. 想去苏州乐园的学生有12人
C. 想去苏州乐园的学生肯定最多
D. 想去苏州乐园的学生占全班学生的![]()
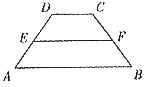
7. 如图所示,已知等腰梯形ABCD的中位线EF的长为6,腰AD的长为5,则该等腰梯形的周长为( )
A. 11 B. 16 C. 17 D. 22
8. 如图所示的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:
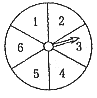
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
其中,你认为正确的见解有:()
A. 1个 B. 2个 C. 3个 D. 4个
第II卷(非选择题,共96分)
二. 填空题:本大题共8小题,每小题3分,共24分,把答案填在题中横线上。
9. ![]() 的相反数是____________。
的相反数是____________。
10. 如图所示,等腰△ABC的顶角为120°,腰长为10,则底边上的高AD=_________。
11. 温家宝总理有一句名言:“多么小的问题,乘以13亿,都会变得很大;多么大的经济总量,除以13亿,都会变得很小。”据国家统计局公布,2004年我国淡水资源总量为26520亿立方米,居世界第四位,但人均只有__________立方米,是全球人均水资源最贫乏的十三个国家之一。
12. 函数![]() 中自变量x的取值范围是____________。
中自变量x的取值范围是____________。
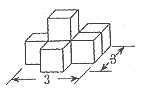
13. 下图的几何体由若干个棱长为1的正方体堆放而成,则这个几何体的体积为_______。
14. 下表给出了苏州市2005年5月28日至6月3日的最高气温,则这些最高气温的极差是______________℃。
 15.
已知反比例函数
15.
已知反比例函数![]() ,其图像在第一、第三象限内,则k的值可为________。(写出满足条件的一个k的值即可)
,其图像在第一、第三象限内,则k的值可为________。(写出满足条件的一个k的值即可)
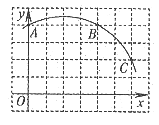
16. 如图所示,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为_____________。
三. 解答题:本大题共12小题,共72分,解答应写出必要的计算过程、推算步骤或文字说明。(第17~19题,每题5分,共15分)
17. 不使用计算器,计算:![]()
18. 化简:![]()
19. 解方程组: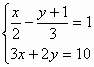
(第20�21题,每题6分,共12分)
20. 如图所示,平行四边形纸条ABCD中,E、F分别是边AD、BC的中点,张老师请同学们将纸条的下半部分平行四边形ABFE沿EF翻折,得到一个V字形图案。
(1)请你在原图中画出翻折后的图形平行四边形A”B”FE;(用尺规作图,不写画法,保留作图痕迹)
(2)已知![]() 的大小。
的大小。
21. 如图所示,小明、小华用4张扑克牌玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
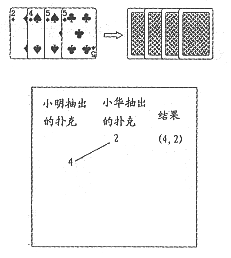
(1)若小明恰好抽到了黑桃4。
①请在右边方框中绘制这种情况的树状图;
②求小华抽出的牌的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌的牌面数字比小华的大,则小明胜;反之,则小明负,你认为这个游戏是否公平?说明你的理由。
(第22�23题,每题6分,共12分)
22. 如图所示,AB是圆O的直径,BC是圆O的切线,D是圆O上的一点,且AD//CO。
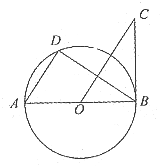
(1)求证:![]() ;
;
(2)若AB=2,![]() ,求AD的长。(结果保留根号)
,求AD的长。(结果保留根号)
23. 为缓解“停车难”问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE。(精确到0.1m)
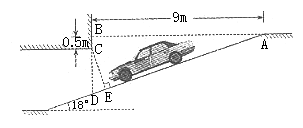
(第24�25题,每题6分,共12分)
24. 已知二次函数![]() 。
。
(1)求证:对于任意实数m,该二次函数图像与x轴总有公共点;
(2)若该二次函数图像与x轴有两个公共点A、B,且A点坐标为(1,0),求B点坐标。
25. 苏州市区某居民小区共有800户家庭,有关部门准备对该小区的自来水管网系统进行改造,为此,需了解该小区的自来水用水情况。该部门通过随机抽样,调查了其中的30户家庭,已知这30户家庭共有87人。
(1)这30户家庭平均每户___________人;(精确到0.1人)。
(2)这30户家庭的月用水量见下表:
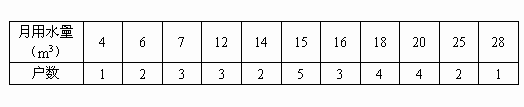
求这30户家庭的人均日用水量;(一个月按30天计算,精确到0.001m3)
(3)根据上述数据,试估计该小区的日用水量?(精确到1m3)
26. (本题6分)
(1)如图1所示,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连结AE。求证:AE//BC;
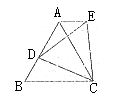
图1
(2)如图2所示,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形,所作△EDC改成相似于△ABC。请问:是否仍有AE//BC?证明你的结论。
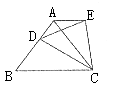
图2
27. (本题7分)
苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
(1)每亩水面的年租金为500元,水面需按整数亩出租;
(2)每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
(3)每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
(4)每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
①若租用水面n亩,则年租金共需__________元;
②水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
③李大爷现有资金25000元,他准备再向银行贷不超过25000元的款,用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35000元?
28. (本题8分)
如图1所示,平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6),D是BC边上的动点(与点B、C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,将△BDE沿DE翻折,得到△GDE,并使直线DG、DF重合。
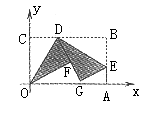
图1
(1)如图2所示,若翻折后点F落在OA边上,求直线DE的函数关系式;
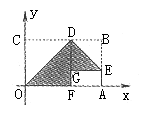
图2
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线![]() 的公共点的个数,在图2的情形中通过计算验证你的猜想;如果直线DE与抛物线
的公共点的个数,在图2的情形中通过计算验证你的猜想;如果直线DE与抛物线![]() 始终有公共点,请在图1中作出这样的公共点。
始终有公共点,请在图1中作出这样的公共点。
【试题答案】
2005年苏州市初中毕业暨升学考试
数学试题参考答案
一. 选择题(每题3分,共24分)
1. B 2. C 3. B 4. A
5. D 6. D 7. D 8. A
二. 填空题(每题3分,共24分)
9. ![]() 10.
10.
![]() 11.
2040
11.
2040
12. ![]() 13.
6 14. 7
13.
6 14. 7
15. 答案不惟一,只要符合k>2即可;
16. (2,0)
三. 解答题(共72分)
17. (5分)
解:原式![]()
18. (5分)
解法一:原式![]()
解法二:原式![]()
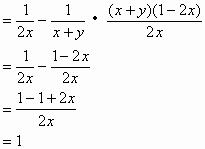
19. (5分)
解:整理,得![]()
![]() ,即
,即![]()
将![]() 代入(2)式,得
代入(2)式,得![]() ,即
,即![]()
∴原方程组的解为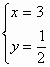
20. (6分)
解:(1)画出正确的图形(见图)。
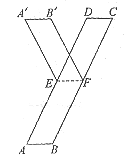
有正确的作图痕迹。
(2)![]()

21. (6分)
解:(1)①见下图
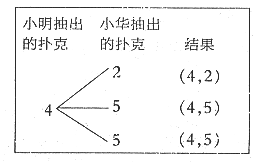
②小华抽出的牌的牌面数字比4大的概率是![]() 。
。
(2)这个游戏不公平。
小明胜的情况共有5种,即(4,2),(5,2),(5,2),(5,4),(5,4),故小明获胜的概率为![]() ,而小明输的概率为
,而小明输的概率为![]() 。
。

22. (6分)
(1)证明:∵AB是圆O的直径
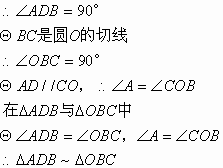
(2)解:由(1),得![]()
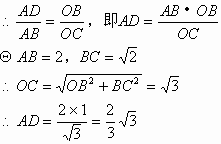
注1:结果写成![]() 不扣分,结果取近似值不得分。
不扣分,结果取近似值不得分。
注2:本题也可以利用垂径定理求解。
23. (6分)
解:在△ABD中,![]()
![]()
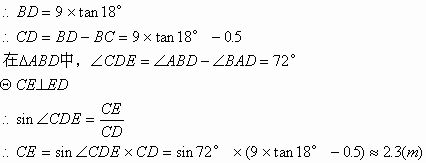
答:CE为2.3m。
24. (6分)(1)证明:![]()
![]()
∴对于任意实数m,该二次函数图像与x轴总有公共点。
(2)解:把(1,0)代入二次函数关系式,得:
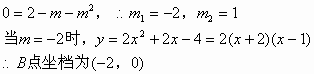
当![]() 时,
时,![]()
![]()
25. (6分)
(1)2.9
(2)解:![]() +25×2+
+25×2+![]() 。
。
![]() 。
。
答:这30户家庭的人均日用水量为0.174m3
(3)解:![]()
(或:![]() )
)
答:估计该小区每天需要使用![]() 自来水。
自来水。
26. (6分)
(1)证明:![]() 都是等边三角形
都是等边三角形
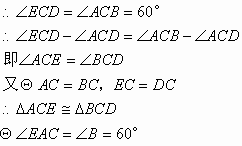
![]()
![]()
(2)仍有AE//BC
证明:![]()
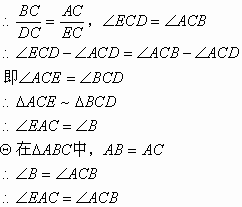
![]()
27. (7分)
(1)500n
(2)解:每亩的成本![]()
每亩的利润![]()
(3)解:设向银行贷款x元。
则![]()
即![]()
根据题意,有
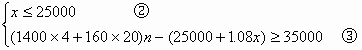
将![]()
即![]()
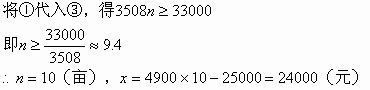
答:李大爷应该租10亩水面,并向银行贷款24000元。
注:③也可以列成![]() 。
。
28. (8分)
(1)解:根据题意,可知![]()
∴直线DE的函数关系式为![]()
(2)解:根据题意,可知![]()
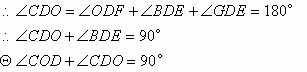
![]()
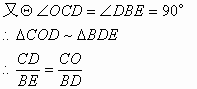
根据题意,可知![]()
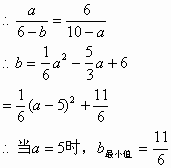
(3)猜想:直线DE与抛物线![]() 只有1个公共点。
只有1个公共点。
证明:由(1)可知,DE所在直线为![]()
代入抛物线![]() ,消去y,得
,消去y,得![]()
化简,得![]()
![]()
∴直线DE与抛物线![]() 只有1个公共点。
只有1个公共点。
作法一:延长OF交DE于点H。
作法二:在DB上取点M,使DM=CD,过M作![]() ,交DE于点H。
,交DE于点H。