2006年中考全真模拟试卷（四）
（考试时间：120分钟 满分150分）
| 题号 | 一 （1-12） | 二 （13-18） | 三 | 总分 | 积分人 | 核分人 | |||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | ||||||
| 得分 | |||||||||||||
| 得分 | 评卷人 |
一、选择题（每题3分，共36分.每小题有四个选项，其中只有一个选项是正确的，将正确选项的字母填入下表相应的题号下面.）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．小明放学回家将自行车放于地下1楼车库，来到1楼奶奶家帮助做了一会儿家务，然后回到三楼自己的家中，他一共爬的楼层数可列式计算为
A．3―（―1）＝4 Ｂ．3－1＝２
Ｃ．２―（―1） ＝3 Ｄ．―1 ―3＝－4
2．水是由氢原子和氧原子组成的，其中氧原子的直径是0.米，用科学记数法可表示为
A．0.74×10－10 米 Ｂ．74×10－12米
Ｃ．7.4×10－10米 Ｄ．7.4×10－11米
3．下列计算中，正确的是
A．3a+5b=8ab Ｂ．(—ab)3＝－a3b3 Ｃ．a6÷a2＝a3 Ｄ． x3＋x3=x6
4．下图中几何体的左视图是
 |
5．小斌家买了一套新房正在进行装修，星期天小斌陪父母一起到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设客厅地面（需无缝），则购买的瓷砖形状不可以是
A.三角形地砖 B.正方形地砖 C. 正六边形地砖 D. 正五边形地砖
6．家在农村的小李家卖猪，为了揭露收购者短斤少两的行为，在收购者称一头猪重207斤并还没有被放下的时候，快速在猪身上放了事先称好的准确的10斤重的铁块，结果称得216斤。假设猪的实际重x斤，则根据题意，列方程得
A．
Ｂ．
Ｃ．
Ｄ．
7． 同时向空中掷两枚质地完全相同的硬币，则出现同时正面朝上的概率为
A． 
Ｂ．
Ｃ．
Ｄ．1
8．平面直角坐标系中，某点在第二象限且它的横坐标、纵坐标之和为2，则该点的坐标是
A．（-1，2） Ｂ．（-1，3） Ｃ．（4，-2） Ｄ．（0，2）
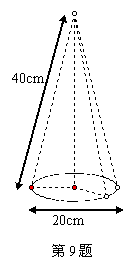
9．劳技课上，王芳制作了一个圆锥形纸帽，其尺寸如图．则将这个纸帽展开成扇形时的圆心角等于
A．45° Ｂ．60° C．90° Ｄ．120°
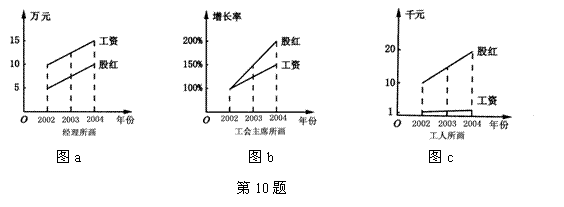
10．某企业有5名正副经理，100名工人，年底公布经营业绩，如下表所示：
| 2002年 | 2003年 | 2004年 | |
| 5名正副经理红利总额 | 5万元 | 7.5万元 | 10万元 |
| 100名工人工资总额 | 10万元 | 12.5万元 | 15万元 |
你认为最恰当的是
A．经理所画的图a Ｂ．工会主席所画的图b
C．工人所画的图c Ｄ．都正确，只不过考虑的角度不同
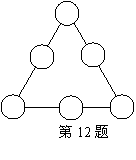
11．如图，平行四边形ABCD的面积为24，E为AB上的中点，连接CE、DE，DE、AC的交点为O，则三角形OCE的面积为
A．2 Ｂ．3 Ｃ．4 Ｄ．6
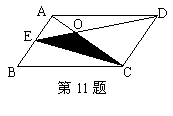
12．如图，在一个由6个圆圈组成的三角形里，把1到6这6个数分别填入图的圆圈中，要求三角形的每条边上的三个数的和S都相等，那么S的最大值是
A．9 Ｂ．10 Ｃ．12 Ｄ．13
 | |||
 | |||
| 得分 | 评卷人 |
二、填空题 (每小题4分，共24分.请把答案填在相应的横线上.)
13．当x=2005时，化简
+2 = ．
14．两圆半径分别为2、3，两圆圆心距为d，则两圆相交时d的取值范围为 ．
15．甲、乙两名学生进行射击练习，两人在相同条件下各射靶10次,将射击结果作统计分析如下:
| 命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
| 乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
请你从射击稳定性方面评价甲、乙两人的射击水平，则 比较稳定.
16．若反比例函数
与一次函数
的图象都经过点A（a，2），则m= .
17．如上图，Rt△AOB的斜边OA在y轴上，且OA=5，OB=4，将Rt△AOB绕原点O逆时针旋转一定的角度，使直角边OB落在x轴的负半轴上，得相应的△A’OB’，则A’点的坐标是 ．
18．在课题学习时，老师布置画一个三角形ABC，使∠A=30°，AB=10cm, ∠A的对边可以在长为4cm、5cm、6cm、11cm四条线段中任选，这样的三角形可以画 个．
三、解答题 (本大题共8题，计90分.解答时应写明演算步骤、证明过程或必要的文字说明.)
| 得分 | 评卷人 |
19．(本题满分8分)
阅读下面对话:
小红妈: “售货员，请帮我买些梨. ”
售货员: “小红妈，您上次买的那种梨都卖完了，我们还没来得及进货，我建议这次您买些新进的苹果，价格比梨贵一点，不过苹果的营养价值更高. ”
小红妈: “好，你们很讲信用，这次我照上次一样，也花30元钱. ”
对照前后两次的电脑小票， 小红妈发现: 每千克苹果的价是梨的1.5倍，苹果的重量比梨轻2.5千克.
试根据上面对话和小红妈的发现，分别求出梨和苹果的单价.
| 得分 | 评卷人 |
20．(本题满分10分)
小宝和爸爸、妈妈3人玩跷跷板，3人体重一共为150千克，爸爸坐在跷跷板的一端，体重只有妈妈一半的小宝和妈妈一同坐在跷跷板的另一端，这时，爸爸的那端仍然着地，后来，小宝借来一副质量为10千克的哑铃，加在他和妈妈的一端，结果，爸爸被跷起离地。试求确定小宝体重的范围．
| 得分 | 评卷人 |
21． (本题满分10分)
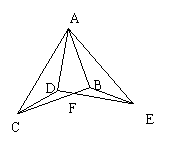
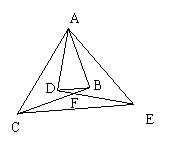
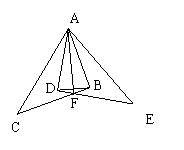
已知：如图，Rt△ABC≌Rt△ADE，∠ABC＝∠ADE=900，试以图中标有字母的点为端点，连结两条线段，如果你所连结的两条线段满足相等、垂直或平行关系中的一种，那么请你把它写出来并证明．
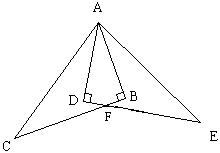
| 得分 | 评卷人 |
22．(本题满分12分)
学校门口经常有小贩搞摸奖活动．某小贩在一只黑色的口袋里装有只有颜色不同的50只小球，其中红球1只，黄球2只，绿球10只，其余为白球．搅拌均匀后，每2元摸1个球．奖品的情况标注在球上（如下图）．
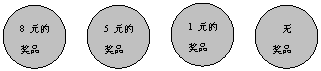（1）如果花2元摸1个球，那么摸不到奖的概率是多少？
（2）如果花4元同时摸2个球，那么获得10元奖品的概率是多少？
| 得分 | 评卷人 |
23．(本题满分12分)
某课外学习小组在设计一个长方形时钟钟面时，欲使长方形的宽为20厘米，时钟的中心在长方形对角线的交点上，数字2在长方形的顶点上，数字3、6、9、12标在所在边的中点上，如图所示。
（1）问长方形的长应为多少？
（2）请你在长方框上点出数字1的位置，并说明确定该位置的方法；
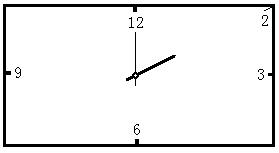（3）请你在长方框上点出钟面上其余数字的位置，并写出相应的数字（说明：要画出必要的、反映解题思路的辅助线）。
| 得分 | 评卷人 |
24、(本题满分12分)
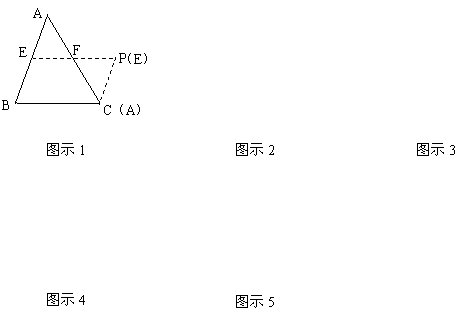
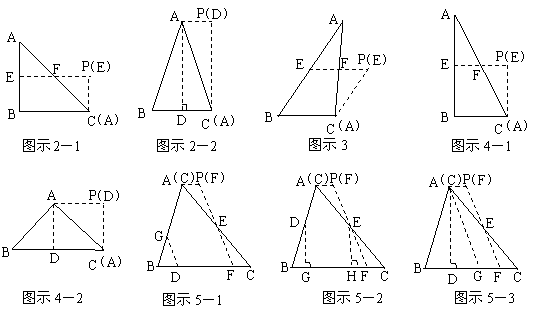
在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF一刀剪切后，用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图示1，仿上述的方法，按要求完成下列操作设计，并在规定位置画出图示，
⑴在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置；
⑵在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置；
⑶在△ABC中，增加条件＿＿＿＿＿＿＿＿＿＿＿＿＿，沿着＿＿＿＿＿一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置
⑷在△ABC（AB≠AC）中，一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，其操作过程（剪切线的作法）是：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
然后，沿着剪切线一刀剪切后可以拼成等腰梯形，剪切线与拼图画在图示5的位置.
| 得分 | 评卷人 |
25、(本题满分12分)
扬州亚龙水果批发市场内有一种水果，保鲜期一周，如果冷藏，可以延长保鲜时间，但每天仍有一定数量的这种水果变质，假设这种水果保鲜期内的个体重量基本保持不变。现有一个体户，按市场价收购了这种水果200千克放在冷藏室内，此时市场价为每千克2元，据测算，此后这种鲜水果每千克的价格每天可上涨0.2元，但存放一天需各种费用20元，日平均每天还有1千克变质丢弃.
(1)设x天后每千克鲜水果的市场价为y元，写出y关于x的函数关系式；
(2)若存放x天后将鲜水果一次性出售，设鲜水果的销售总金额为w元，写出w关于x的函数关系式；
(3)该个体户将这批水果存放多少天后出售，可获最大利润Q?最大利润Q是多少?
(本题不要求写出自变量x的取值范围)
| 得分 | 评卷人 |
26、(本题满分14分)
已知，O为正方形ABCD对角线上一点，以O为圆心，OA的长为半径的⊙O与BC相切于M，与AB、AD分别相交于E、F。
(1)求证：CD与⊙O相切．
(2)若正方形ABCD的边长为1，求⊙O的半径。
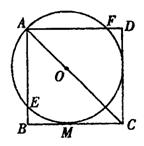(3)对于以点M、E、A、F以及CD与O⊙的切点为顶点的五边形的五条边，从相等的关系考虑，你可以得出什么结论?请你给出证明.
2006年中考全真模拟试卷（四）参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | B | A | D | C | A | B | C | D | C | C |
二、填空题
13、2005 14、1<d<5 15、乙 16、2 17、（-4，3） 18、4
三、解答题
19、解：设梨的单价为x元/千克，苹果的单价为1.5x元千克
30/x - 30/（1.5x）=2.5
解得：x=4
经检验：x=4是原方程的解
∴x=4,1.5x=6
答：梨和苹果的单价分别为4元/kg和6元/kg。
20、解：设小宝体重为xkg，则妈妈体重为2xkg，爸爸体重为（150-3x）kg
x+2x<150-3x
x+2x+10>150-3x
解得：231/3 < x < 25
答：小宝的体重范围为大于231/3kg小于25kg。
21、第一种：连结CD、BE，得：CD=BE
∵△ABC≌△ADE，∴AD=AB，AC=AE
∠CAB=∠EAD
∴∠CAD=∠EAB
∴△ABE≌△ADC
∴CD=BE
第二种：连结DB、CE得：DB∥CE
∵△ABC≌△ADE，∴AD=AB，∠ABC=∠ADE
∴∠ADB=∠ABD，∴∠BDF=∠FBD
同理：∠FCE=∠FEC
∴∠FCE=∠DBF
∴DB∥CE
第三种：连结DB、AF；得AF⊥B D
∵△ABC≌△ADE，∴AD=AB，∠ABC=∠ADE=90°
又AF=AF，∴△ADF≌△ABF
∴∠DAF=∠BAF
∴AF⊥BD
 |
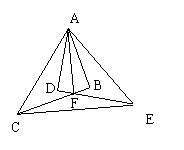第四种：连结CE、AF；得AF⊥CE
∵△ABC≌△ADE，∴AD=AB，AC=AE
∠ABC=∠ADE=90°
又AF=AF，∴△ADF≌△ABF
∴∠DAF=∠BAF ，∴∠CAF=∠EAF
∴AF⊥BD
22、(1)∵白球的个数为50－1－2－10=37
∴摸不到奖的概率是：
（2）获得10元的奖品只有一种可能即同时摸出两个黄球
∴获得10元奖品的概率是：
=
23、⑴ 长方形的长为
⑵⑶ 要画出必要的、反映解题思路的辅助线
24、解：⑴ 方法一：∠B＝90°，中位线EF，如图示2－1.
方法二：AB＝AC，中线（或高）AD，如图示2－2.
⑵ AB＝2BC（或者∠C＝90°，∠A＝30°），中位线EF，如图示3.
⑶ 方法一：∠B＝90°且AB＝2BC，中位线EF，如图示4－1.
方法二：AB＝AC且∠BAC＝90°，中线（或高）AD，如图示4－2.
⑷ 方法一：不妨设∠B＞∠C，在BC边上取一点D，作∠GDB＝∠B交AB于G，过AC的中点E作EF∥GD交BC于F，则EF为剪切线.如图示5－1.
方法二：不妨设∠B＞∠C，分别取AB、AC的中点D、E，过D、E作BC的垂线，G、H为垂足，在HC上截取HF＝GB，连结EF，则EF为剪切线.如图示5－2.
方法三：不妨设∠B＞∠C，作高AD，在DC上截取DG＝DB，连结AG，过AC的中点E作EF∥AG交BC于F，则EF为剪切线.如图示5－2.
25、解：⑴y=2+0.2x
⑵w=(200-x)(2+0.2x)=-0.2x2+38x+400
⑶利润Q=w-20x-400
=-0.2x2+38x+400-20x-400
=-0.2x2+18x
∵-b/（2a）=-18/-0.4=45
（4ac-b2）/4a=-324/-0.8=3240/8=405
∴项点坐标为（45，405）
又∵a=-0.2<0
∴当存放天数为45天时，可获得最大利润为405元。
26、(1)连结OM，作ON⊥CD于N
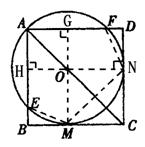∵⊙O与BC相切 ∴OM⊥BC
∵四边形ABCD是正方形 ∴AC平分∠BCD
∴OM=ON ∴CD与⊙O相切
(2)∵四边形ABCD是正方形
∴AD=CD=1，∠D=90°，∠ACD=45°
∴AC=
，∠NOC=45°=∠ACD
∴NC=OC=OA
∴OC=
=ON=OA
∵AC=AO+OC= ∴AO+AO= ∴OA=2-
(3)ME=FN，AE=AF
证明：作OG⊥AD，OH⊥AB
∵AC平分∠BAD ∴OG=OH ∴AE=AF
∵AD=AB ∴DF=BE
∵CD、CB与⊙O相切 ∴CM=CN ∵BC=DC ∴BM=DN
又∵∠B=∠D=90° ∴△EBM≌△FDN ∴EM=FN.