| 浙江省绍兴市2001年中考试题中一道颇有难度的综合性平几题。细致研究可发现此题解法灵活多样,思路宽广,涉及知识多,综合性强,不失为考查学生思维能力的一道难得的几何佳题。现给出它的几种不同的解法,供读者参考。
题目:如图1,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm的速度沿着线段CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,⊙O的半径是( )
A、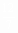 cm B、 cm B、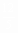 cm C、 cm C、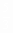 cm D、2cm cm D、2cm
一、相似三角形与面积
解法一:在Rt△ABC中,∵AB=10cm,AC=8cm,∴BC=6cm。∵PC=4cm,∴PA=4cm。设OD=x,⊙O的半径为r,∵OD∥AC,∴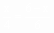 。∴x=4- 。∴x=4-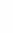 r。 r。
∵S△ABC=S△AOC+ S△BOC+ S△AOB
∴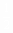 ×10r+ ×10r+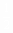 ×8r+ ×8r+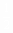 ×6r= ×6r= ×6×8。 ∴5r+4r+3(4- ×6×8。 ∴5r+4r+3(4- r)=24,∴r= r)=24,∴r=
 (图1) (图1) 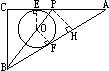 (图2) (图2)
解法二:如图2,在Rt△ABC中,∵AB=10cm,AC=8cm,
∴BC=6cm
∵P是AC的中点,
∴S△ABP=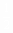 ×S△ABC=12 ×S△ABC=12
∴AB×PH=24,PH=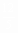
∵OE∥BC,OF∥PH,
∴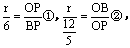
由①+②得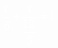
∴r=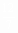
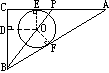 (图3) (图3) 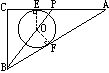 (图4) (图4)
二、相似三角形与勾股定理
解法三:如图3,设OD=x,⊙O的半径为r,∵OD∥AC,∴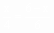 。 。
∴x=4-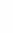 r ① r ①
∵AE=AF=8-x,∴BF=2+x
∴OD2+BD2=OF2+BF2,
∴x2+(6-x)2=r2+(2+x)2,
∴x=8-3r ②
由①、②得4-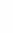 r=8-3r,解得r= r=8-3r,解得r=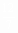 . .
三、三角函数与勾股定理
解法四:如图4,设PE=x,⊙O的半径为r
∵tg∠CDB= ,∴x= ,∴x=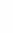 r, r,
由勾股定理得:PO=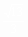 r,∴BO=2 r,∴BO=2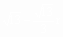 , ,
∴AF=AE=4+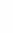 r,∴BF=6- r,∴BF=6-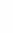 r, r,
∵OB2=OF2+BF2,∴(2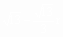 )2=r2+(6- )2=r2+(6-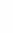 r)2 r)2
解得r=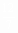
四、三角形内角平分线性质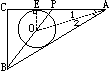
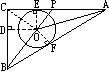
解法五:如右图,∵AE、AF是⊙O的切线,
∴∠1=∠2,
∴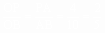 , ,
∴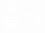
∵OE∥BC,∴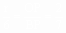 ,∴r= ,∴r= 载自《理科考试研究》初中 |