初三数学中考数学模拟卷（-）

一、下列各题均有四个选项，其中只有一个是正确的.(本题共48分，每小题4分)

1.4的算术平方根是(　　　)

A.2　　B.－2　　C.±2　　D.16

2.如果一个角等于36°，那么它的余角等于(　　  )

A.64° B.54°　 C.144°　D.36°

3.点P(1，－2)关于原点对称的点的坐标是(　　　)

A.(－1，2)　　B.(－1，－2)　　C.(－2，－1)　　D.(1，2)

4.在函数中，自变量x的取值范围是(　　　)

A.x≥2　　B.x＞2　　C.x＞－2　　D.x≠2

5.下列图形中，是轴对称图形但不是中心对称图形的是(　　  )

A.菱形　　B.矩形　　C.等边三角形　　D.圆

6.19990用科学记数法表示为(　　　)

A.19.99×10²　　B.199.9×10²　　C.1.999×10⁴　　D.1.999×10^-4

8.如果数据1，3，x的平均数是3，那么x等于(　　　)

A.5　　B.3　　C.2　　D.－1

9.如果两圆半径分别为3cm和5cm，圆心距为2cm，那么这两个圆的位置关系为(　　  )

A.外离　　B.外切　　C.相交　　D.内切

10.如图，ABCD为圆内接四边形，E是AD延长线上一点，如果∠B=60°，那么∠EDC等于(　　　)

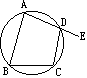
A.120°　　B.60°　　C.40°　　D.30°

11.如果反比例函数y=k/x的图象经过点(-4,-5)，那么这个函数的解析式为(　　　)

12.如果一个多边形的内角和等于它的外角和的2倍，那么这个多边形的边数为(　　　)

A.3　　B.4　　C.5　　D.6

二、填空题（共30分）

1、分解因式：x²-5x-14＝________。

2、将一个四边形沿一条直线对折后，两边的图形完全重合，如菱形沿它的对角线所在的直线对折后，两边的图形完全重合；正方形沿对角线所在直线对折也是这样。请你再写出两个这样的四边形，并指出其折痕所在________。

3、已知梯形ABCD中，AD∥BC，AC、BD交于O点，若，则＝________。

4、某商场销售一批电视机，一月份每台毛利润是售出价的20％（毛利润＝售出价－买入价），二月份该商场将每台售出价调低10％（买入价不变），结果销售台数比一月份增加120％，那么二月份的毛利润总额与一月份毛利润总额的比是　　　　  。

5、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为　　　　　　　

三、解答下列各题（共72分）　　　　　　　　　  　　　　　　　　　　　　

　1、计算：2cos30°-(-4)^-1++　（8分）

2、解方程:(x+3)(x-1)=5　 （8分）

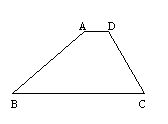
3. 如图：水坝的截面为梯形ABCD，坝顶宽AD＝6米，坡面DC米，AB的坡度为，

　　求：水坝截面的面积。（10分）

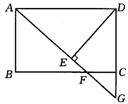
4、如图3，在矩形 ABCD中，F是BC边上一点，AF的延长线交DC的延长线于G，DE⊥AG于E，且DE＝DC．根据上述条件，请在图中找出一对全等三角形，并证明你的结论．（10分）

5、有一个附有进出入管的容器，每单位时间内进出的水量都是一定的，设从某时刻开始的4分钟内只进水，不出水，在随后的8分钟内既进水又出水，得到时间x（分）与水量y（升）之间的关系如图所示.

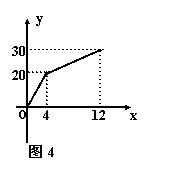（1）每分钟进水多少？（3分）

（2）4≤x≤12时，x与y有何关系？（4分）

（3）若12分钟后只放水，不进水，求y的表达式.（4分）

6、在探索图形的面积的时候，王老师带学生们去测量一个环行花坛的面积，学生们想出了多种方法，下面是一段学生的对话：

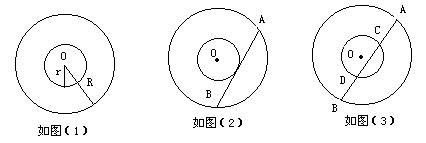
甲说：如图（1）只要测出大圆和小圆的半径R、r就可以求出环行花坛的面积了；

乙说：如图（2）要找圆心比较麻烦，我只要找一根直棒，让它和小圆相切，再测出它与外圆两交点A、B的长度AB就可以求出环形花坛的面积。

 （1）、试用你学习过的知识说明乙同学的理由；

 （2）、如图（3）在两同心圆中大圆的弦AB交小圆于C，D两点，已知AB=16cm，DC=7cm，求圆环的面积。（12分）

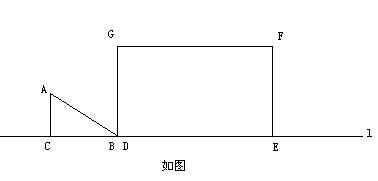
7、如图Rt⊿ABC与矩形DEFG在同一l直线上，∠ACB=90⁰，AC=3cm，AB=5cm，DE=8cm，DF=6cm，现⊿ABC从图（1）位置出发，以1cm/秒的速度向右平移。设运动时间为t秒，重叠部分的面积为Scm²。

（1）　  当运动2秒钟时，求重叠部分的面积；（4分）

（2）　  是否存在某一时刻，重叠部分的面积不变，若存在，求出持续不变的时间；若不存在，试说明理由；（4分）

（3）　  分别求出0≦t≦4，8≦t≦12时的S关于t的函数关系式（6分）