2006年初三数学中考模拟测试题 (F.)
(考试时间:120分钟,满分120分)
一、填空题(本题目有10个小题,每小题2分,共20分)
1.据新华社报道:2010年我国粮食产量将达到540 000 000 000千克,用科学记数法可表示为_____ ____千克.
2. 若![]() ,则
,则![]() =
.
=
.
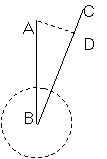
![]() 3. 如图,有一个透明的圆柱形状的玻璃杯,由内部测得其底面半径为3cm,高为 8cm,今有一支12cm的吸管任意斜放于杯中,若不考虑吸管的粗细,吸管露出杯口长度最少为 cm.
3. 如图,有一个透明的圆柱形状的玻璃杯,由内部测得其底面半径为3cm,高为 8cm,今有一支12cm的吸管任意斜放于杯中,若不考虑吸管的粗细,吸管露出杯口长度最少为 cm.
4.若![]() ,则
,则![]() .
.
5.某商场5月份一周的利润情况如下表:
| 日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 | 8日 |
| 当日利润/万元 | 0.20 | 0.24 | 0.23 | 0.23 | 0.21 | 0.19 | 0.17 |
 根据上表,估计该商场今年5月份的总利润是
万元.
根据上表,估计该商场今年5月份的总利润是
万元.
6.一只口袋中有红色、黄色和蓝色玻璃球共72个,小明通过多次摸球实验后发现摸到红色、黄色和蓝色球的概率依次为35%、25%和40%,则口袋中有红球、黄球、和蓝球的数目很可能是 个、 个和_______个.
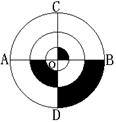
7.如图,AB=4cm,CD⊥AB于O,则图中阴影部分的面积为 cm2.
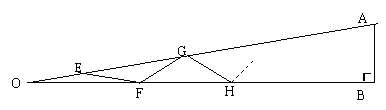
 8.如图,Rt△AOB是一钢架,且∠AOB=100,为了让钢架更加坚固,需要在其内部添加一些钢管EF、FG、GH、…等,添加的钢管长度都与OE相等,那么最多能添加这样的钢管_ 根.
8.如图,Rt△AOB是一钢架,且∠AOB=100,为了让钢架更加坚固,需要在其内部添加一些钢管EF、FG、GH、…等,添加的钢管长度都与OE相等,那么最多能添加这样的钢管_ 根.
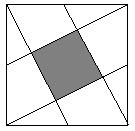
9.如图,E、F、G、H分别是正方形ABCD各边中点,要使中间阴影部分小正方形的面积是5,那么大开放型的边长应该是 .
10.科学研究发现:植物的花瓣、片、果实的数目以及其它方面的特征,都非常吻合于一个奇特的数列——裴波那契数列:1,1,2,3,5,8,13,21,34,55,…,仔细观察以上数列,则它的第11个数应该是 .
二.选择题(本题有10小题,每小题3分,共30分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
11.![]() ( )
( )
A、![]() B、21 C、20 D、6
B、21 C、20 D、6
12. 在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是 ( )
A B C D
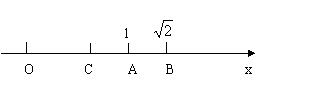 13.如图,数轴上表示1,
13.如图,数轴上表示1, ![]() 的对应点分别为A、B,点B关于点A的对称点为C,则点C所表示的数是
( )
的对应点分别为A、B,点B关于点A的对称点为C,则点C所表示的数是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14.如果a≠0,且a、b互为相反数,则在下列各组数中,不是互为相反数的一组是( )
A 、![]() B、
B、![]() C、3a与3b D、a+1与b-1
C、3a与3b D、a+1与b-1
15.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若ABC的周长为12,则PD+PE+PF= ( )
 A、12 B、8 C、4
D、3
A、12 B、8 C、4
D、3
|
|
16.如图,D、E分别是⊙O半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则弧AC的长与弧CB的长的大小关系是 ( )
A、弧AC=弧CB B、弧AC>弧CB C、弧AC<弧CB D、不能确定
17.抛物线y=2x2-3x+1的顶点坐标为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
18.如图1,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下部分剪拼成一个矩形(如图2),通过计算阴影部分的面积,可以验证的等式为( )
A、a2-ab=a(a-b) B、(a-b)2= a2-2ab+b2 C、(a+b)2= a2+2ab+b2 D、a2-b2=(a+b)(a-b)
 |
19.如图,平行四边形ABCD的对角线AC上有E、F两点,且AE=CF,则图中全等的三角形对数有 ( )
A、3对 B、4对 C、5对 D、6对
20.一本书共有250页,随手将其翻开,右边一页的页码恰是5的倍数的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三、解答题:(21,22每小题6分,23,24每小题8分,25,26每小题9分, 27,28每小题12分,共70分)
21. ![]() .
.
22. ![]()
23.根据算式中数的变化,请你认真填写运算符号和括号.
解:10 30 20 20 60 15
=300 20 20 4
=14 4
=10.
24.九年级(3)班的一个综合实践活动小组去A、B两家超市调查去年和今年“五一节”期间的销售情况,下图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话请你分别求出A、B两家超市今年“五一节”期间的销售额.

25.某校射击队在相同的条件下对甲乙两名运动员进行了10次射靶测试,成绩如下:
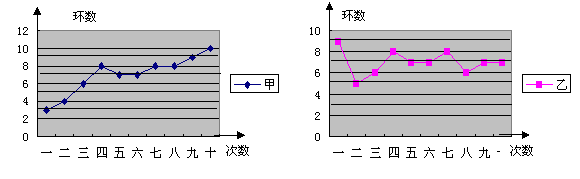
(1)请根据图中信息完成下表:
| 项目 | 平均数 | 中位数 | 方差 | 6.5-7.5环的频数 | 6.5-7.5环的频率 |
| 甲 | 7 | 4.2 | 0.2 | ||
| 乙 | 7 | 4 |
(2)甲、乙两人谁射靶的成绩比较稳定?请说明理由.
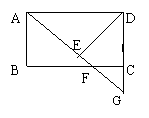
 26. 如图.在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.根据上述条件,请你在图中找出一对全等三角形,并证明你的结论.
26. 如图.在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.根据上述条件,请你在图中找出一对全等三角形,并证明你的结论.
 |
27.台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东300方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
(1) 该城市是否会受到这次台风的影响?为什么?(提示:过A作AD⊥BC于D).
(2) 若受到台风影响,那么台风影响该城市的持续时间有多长?
(3) 该城市受到台风影响的最大风力为几级?,
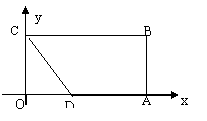
28. 如图.在矩形OABC中,OA=8,OC=4,OA、OC分别在x,y轴上,点O在OA上,且CD=AD.
(1)求直线CD的解析式;
(2)求经过B、C、D三点的抛物线的解析式;
(3)在上述抛物线上位于x轴下方的图象上,是否存在一点P,使△PBC的面积等于矩形的面积?若存在,求出点P的坐标,若不存在请说明理由.
|
一、1、5.4×1011. 2、0.3、2 . 4、34. 5、6.51. 6、25,18,29. 7、π.8、7. 9、5.10、89.
二、11、A. 12、D.13、C.14、B.15、C.16、A.17、B .18、D.19、D. 20、C.
三、21、化简结果2x,值![]()
22、![]()
23、(10×30-20)÷20-(60÷15)=(300-20)÷20-4=14-4=10.
24、解:设A、B超市去年“五一节”期间销售额分别为x,y万元,则
![]()
![]()
![]()
答:该超市今年“五一节”期间销售额分别为115万元和55万元.
25.(1) 甲:7.5,2;乙:7,1.2,0.4.
(2) ∵![]() .∴乙运动员的射靶成绩较为稳定.
.∴乙运动员的射靶成绩较为稳定.
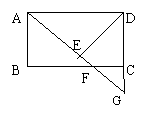 26、△ABF≌△DEA.
26、△ABF≌△DEA.
证明:∵四边形ABCD矩形,
∴AB=CD,AD∥BC, ∠B=90°,
又∵DE=DC,DE⊥AC.
∴∠B=∠DEA=90°,∠AFB=∠DAE,AB=DE.
∴△ABF≌△DEA(AAS).
27、解:(1). 该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
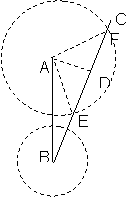 ∵∠OCG=30°,AB=220,∴
∵∠OCG=30°,AB=220,∴![]()
∴受台风影响范围的半径为20×(12-4)=160.
∵110<160. ∴该城市会受到这次台风的影响.
(2)如图,以A为圆心,160为半径作⊙A交BC于E、F.
∴台风影响该市的路程![]()
∴台风影响该市的持续时间为:![]()
(3) ∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12-(110÷20)=6.5(级).
28. 解:(1)设OD=x,则CD=AD=8-x.
∴(8-x) 2-x2=16. ∴x=3. D的坐标是(3,0),又点C的坐标是(0,4),设直线CD的解析式为:y=kx+b,于是有 ![]()
![]()
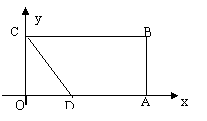 (2)由题意得B、C、D三点坐标分别为(8,4), (0,4), (3,0),设抛物线解析式为
(2)由题意得B、C、D三点坐标分别为(8,4), (0,4), (3,0),设抛物线解析式为![]() 则有
则有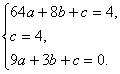
于是可得抛物线解析式为:![]()
(3) 在抛物线上不存在一点P,使△PBC的面积等于矩形ABCD的面积.
理由是: 由抛物线的对称性可知,以抛物线顶点为P的△PBC面积为最大.
由![]() 可知顶点坐标为(
可知顶点坐标为(![]() )
)
则△PBC的高为4+![]()
∴△PBC的面积为![]()
小于矩形ABCD的面积为4×8=32.
故在x轴下方且在抛物线上不存在一点P,使△PBC的面积等于矩形ABCD的面积.
