2005年中考数学模拟试卷

一、　  选择题
1、5的相反数是…………………………（　　　　　　　　 ）
（A）（B）（C）（D）
2、和数轴上的点一一对应的数是………（　　　　　　　　　　　　　　　　）
（A）整数（B）有理数（C）无理数（D）实数
3、下列运算正确的是……………………（　　　　　　　　　　　　　　　　）
（A）　　　（B）
（C）（D）
4、若的乘积中不含的一次项，则的值为……………………………………………（　　　　　　　　　 ）
（A）6（B）（C）0（D）
5、把分解因式的结果是（　　　　　　　　 ）
（A）（B）
（C）（D）
6、已知，化简的结果是（　　　　　　　　　　　　　 ）
（A）（B）（C）（D）
7、不等式组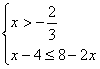的最小整数解是（　　　　　　　　　　　　　　　 ）
（A）（B）0（C）1（D）4
8、3是关于的方程的一个根，则的值是………………………………………………（　　　　　　　　　　）
（A）11（B）12（C）13（D）14
9、给出下列函数：
　　　　　；　　　　　　 ，其中随着的增大而减小的函数是…………………………（　　　　　　　　　　　　）
（A）（1）、（2）　　　　　　　　　　　　　　　　　　　　　　　　（B）（1）、（3）
（C）（2）、（4）　　　　　　　　　　　　　　　　　　　　　　　　（D）（2）、（3）、（4）
10、已知，则二次函数的图象的顶点可能在………（　　　　　　　　　　　　　　　　）
（A）第一或第二象限　　　　　　　　　　　　　　 （B）第三或第四象限
（C）第一或第四象限　　　　　　　　　　　　　　 （D）第二或第三象限
11、如图，有一矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将AED以ED为折痕向右折叠，AE与BC交于点F，则的面积为……………………………………………（　　　　　　　　　　　　　　）

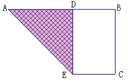
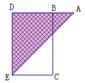
（A）4（B）6（C）8（D）10
12、当锐角时，下列不等式不成立的是（　　　　　　　　　　　　　　　 ）
（A）　　　　　　　　　　　　　 （B）
（C）　　　　　　　　　　　　　　　　　　　　　　　　（D）
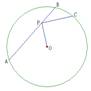
13、如图，点P为弦AB上的一点，连结OP，过点P作，PC交⊙O于点C，若AP=4，PB=2，则PC的长为………………………………（　　　　　　　　　　　　　　 ）
（A）　　　　　　　　　　　　　　（B）
（C）　　　　　　　　　　　　　　　　　　　　　　　　（D）
14、 长度为60cm的一根绳子分别围成一个正三角形、圆、正方形、正六边形，则其中面积最大的是…………（　　　　　　　　　　　　　）
（A）正三角形（B）正方形（C）正六边形（D）圆

15、有如下四个命题：（1）有两边及一角对应相等的两个三角形全等；（2）菱形既是轴对称图形，又是中心对称图形；（3）平分弦的直径垂直于弦，并且平分弦所对的两条弧；（4）两圆的公切线最多有4条.其中真命题的个数为……（　　　　　　　　　　　　　）
（A）1（B）2（C）3（D）4

二、　  填充题
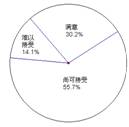
16、2001年中国人民银行统计司就城镇居民对物价水平满意度进行了抽样调查，结果如下图，据此，可估计2001年城镇居民中对物价水平表示认可的约占　　　%

17、写出一个以（-2，3）顶点、开口向下的抛物线解析式　　　　　　　  .
18、若方程的两根的平方和为2，则的值是　　　 .
19、同时使分式有意义，又使分式无意义的的取值范围是　　　　.
20、若等腰梯形一底角为，面积为，中位线长为，则此梯形的周长为　 　　 

三、　  解答题
21、求使方程组的解都是正数的的取值范围
22、在中，点D为线段AC上的一点，且AD=DB， 求的值
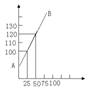
23、科学家通过实验探究出一定质量的某气体在体积不变的情况下，压强P（千帕）随温度t（）变化的函数关系式是P=kt+b，其图象是如图所示的射线AB.
（1）根据图象求出上述气体的压强与温度t的函数关系式
（2）求出当压强P为200千帕时，上述气体的温度
24、阅读材料，解答问题.
　 阅读材料：当抛物线的解析式中含有字母时，随着系数中的字母的取值不同，抛物线的顶点坐标也发生变化.
例如，由抛物线①⑤有。所以，抛物线的顶点坐标即③当的值变化时，的值也随之变化，因而的值也随的值而变化，由③可得④，解答问题：根据阅证券阅读材料提供的方法，确定抛物线顶点的纵坐标与横坐标之间的关系式
25、直线与轴、轴分别交于点M、N（1）求M，N的坐标；（2）如果点P在坐标轴上，以点P为圆心，为半径的圆与直线相切，求点P的坐标
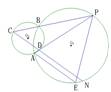
26、已知，圆与圆相交于A、B两点，P是圆上一点，PB的延长线交圆于点C，PA交圆于点D，CD的延长线交圆于点N.（1）过点A作AE//CN，证明：PA=PE；（2）连结PN，若PB=4，BC=2，求PN的长