2005年中考模拟试题

一、选择题(每题3分，共18分)

1、下列计算正确的个数是（ ）

①（-y³）²=y⁶ ②-（-x²）³=-x⁶ ③10⁰÷10³=10^-3

④（a-b）².(b-a)³=(a-b)⁵ ⑤-3⁴=81 ⑥（-0.1）^-1=10

A. 2个 B. 3个 C. 4个 D. 5个

2、某人到瓷砖商店去购买一种多边形形状的瓷砖，用来铺设无缝地板，他购买的瓷砖形状不可以是（ ）

A. 正三角形 B. 矩形 C. 正八边形 D. 正六边形

3、在银行存款准备金不变的情况下，银行的可贷款总量与存款准备金率成反比例关系.当存款准备金率为7.5%时，某银行可贷款总量为400亿元，如果存款准备金率上调到8%时，该银行可贷款总量将减少亿元 ( ).

A. 20 B. 25 C. 30 D. 35

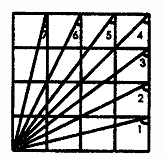
4、在如图所示的正方形网格中．

∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝( )；

A. 145 度 B．180度 C．270度 D．315度

5、星期天晚饭后，小红从家里出去散步，下图描述了他散步过程中离家的距离S(米)与散步所用时间(t)分之间的函数关系。依据图象，下面描述符合小红散步情景的是( )

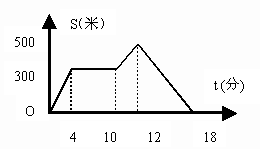
A． 从家出发，到了一个公共阅报栏，看了一会儿报，就回家了.

B．从家出发，到了一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了.

C．从家出发，一直散步(没有停留)，然后回家了.

D．从家出发，散了一会儿步，就找同学去了，18分钟后才开始返回

6、下列图形中，是中心图形又是轴对称图形的有( )

①平行四边形；②菱形；③矩形；④正方形；⑤等腰梯形；⑥线段；⑦角；

A. 2个； B. 3个； C. 4个； D. 5个；

二、填空题：

7、今年6月5日是第34个世界环境日，其主题是“海洋存亡，匹夫有责”。目前全球海洋总面积约为36105.9万平方公里，用科学记数法(保留三个有效数字)表示为平方公里

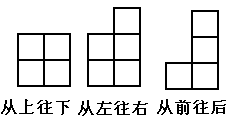
8、由若干个同样大小的正方体堆积成的一个实物，从不同侧面观察到如下投影，则构成该实物的小正方体个数为 .

9、古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为 。

10、若一个圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的圆心角是_________. .

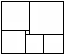
11、如图，一个长方形被划分成如图所示的6个正方形，已知中间的最小的正方形的面积为1平方厘米，则这个长方形的面积为

12、Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，若以C为圆心，以r为半径的圆与AB相切，则r的值为

三、作图题：

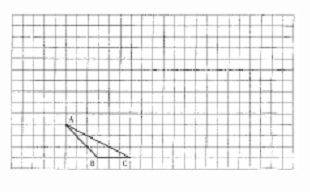
13、（1）请在如图所示的方格纸中，将△ABC向上平移3格，再向右平移6格，得△A₁B₁C₁，再将△A₁B₁C₁绕点B₁按顺时针方向旋转90，得△A₂B₁C₂，最后将△ A₂B₁C₂以点 C₂为位似中心放大到2倍，得△A₃B₃C₂；

（2）请在方格纸的适当位置画上坐标轴（一个小正方形的边长为1个单位长度），在你所建立的直角坐标系中，点C、C₁、C₂的坐标分别为：点C（）、点C₁（ ）、点C₂（ ）.

四、解答题：

14、有这样一道题：“计算：的值，其中．”甲同学把”错抄成“”，但他的计算结果也是正确的．你说这是怎么回事？

15、某校初三(1)班、(2)班各有49名学生，两班在一次数学测验中的成绩统计如下表：

班级	平均分	众数	中位数	标准差
初三(1)班	79	70	87	19.8
初三(2)班	79	70	79	5.2

(1)请你对下面的一段话给予简要分析：初三(1)班的小刚回家对妈妈说：“昨天的数学测验，全班平均79分，得70分的人最多，我得了85分，在班里可算上游了!”

(2)请你根据表中数据，对这两个班的测验情况进行简要分析，并提出教学建议。

16、集市上有一个人在设摊“摸彩”，只见他手拿一个黑色的袋子，内装大小、形状、质量完全相同的白球20只，且每一个球上都写有号码（1－20号）和1只红球，规定：每次只摸一只球。摸前交1元钱且在1��20内写一个号码，摸到红球奖5元，摸到号码数与你写的号码相同奖10元。

（1）你认为该游戏对“摸彩”者有利吗？说明你的理由。

（2）若一个“摸彩”者多次摸奖后，他平均每次将获利或损失多少元？

17、(本题满分8分)公路MN和公路PQ在点P处交汇，且∠QPN=30⁰，点A处有一所中学，AP=160m，一辆拖拉机以 3.6km/h的速度在公路MN上沿PN方向行驶，假设拖拉机行驶时，周围100m以内会受噪声影响，那么，学校是否会受到噪声影响？如果不受影响，请说明理由；如果受影响，会受影响几分钟？

18、(本题满分8分)我市向“手拉手”赠送一批计算机，首批运送270台，现与某物流公司联系，得知用A型汽车若干量刚好装完，用B型汽车不仅少用一辆，而且有一辆车差30台计算机装满。

（1）B型汽车比A型汽车每辆可多装15台，求A、B两种计算机各能装多少台计算机？

（2）已知A型汽车的运费是每辆350元，B型汽车的运费是每辆400元，若运送这批计算机同时用这两种型号的汽车，其中B型车比A型车多用1辆所用运费最节约，按这种方案需A、B两种车各多少辆？运费是多少？

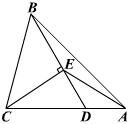
19、（本题满分8分）如图，△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD，E为垂足，连结AE.

(1)写出图中所有相等的线段，并加以证明；

(2)图中有无相似三角形？若有，请写出一对；若没有，请说明理由；

(3)求△BEC与△BEA的面积之比.

20、(本题满分8分)

玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知生产x只玩具熊猫的成本为r(元)，售价每只为p(元)，且r，p与x的关系式分别是r=500+30x， p=170-2x.

(1)当日产量为多少时，每日获得利润为1750元？

(2)日产量为多少时，可获得最大利润？是多少？

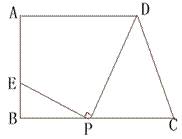
21、(本题满分12分)如图，梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=a，在线段BC上任取一点P，连接DP，作射线PEDP，PE与直线AB交于点E.

(1)试确定CP=3，点E的位置;

(2)若设CP=，BE=，试写出关于自变量的函数关系式;

(3)若在线段BC上能找到不同的两点，使按上述作法得到的点E都与点A重合，试求出此时a的取值范围.

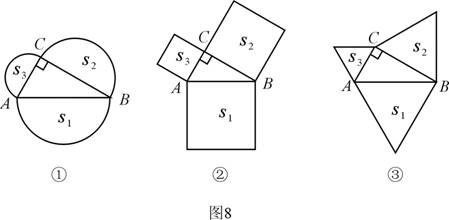
22、(本题满分12分)如下图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S₁、S₂、S₃表示，则不难证明S₁=S₂+S₃ .

(1) 如下图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S₁、S₂、S₃表示，那么S₁、S₂、S₃之间有什么关系？(不必证明)

(2) 如下图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S₁、S₂、S₃表示，请你确定S₁、S₂、S₃之间的关系并加以证明；

(3) 若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S₁、S₂、S₃表示，为使S₁、S₂、S₃之间仍具有与(2)相同的关系，所作三角形应满足什么条件？证明你的结论；

(4) 类比(1)、(2)、(3)的结论，请你总结出一个更具一般意义的结论 .

参考答案

一. 选择题：

1. A 2. C 3. B 4. D 5. B 6. C

二. 填空题：

7. 8. 7个 9. 47 10.

11. 12. 2.4m

三. 作图题

13. 略

四. 解答题：

14. 与x无关

15. 答案略

（以平均分、众数、中位数、标准差4个方面全面分析即可）

16. （1），所以对摸彩者不利

（2）

平均每次损失元

17. 过点A作于D

会影响

以A为圆心100m为半径画弧交MN于E、F

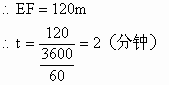
18. （1）设A x台，B （x+15）台

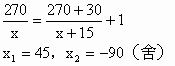
（2）单用A型6辆，费用2100元

单用B型5辆，费用2000元

设A y辆，B (y+1)辆

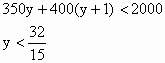
当时，

当时，（台）

所以费用1900元

19. （1）

（2）理由略

（3）

20. （1）解：

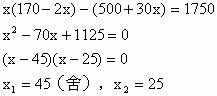
（2）

当时，（元）

21. （1）当，点E与A重合

（2）

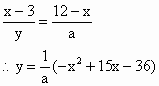
（3）即时，

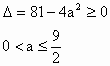
22. （1）

（2）

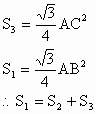
（3）所做三角形必须是正三角形，证明同（2）。

（4）以三边为边向外作正n边形，则有最大正n边形的面积等于其余两个面积之和。