九年级（上）数学期中考试卷

　　　　　　　　　  姓 名 ----------班 级 ---------分 数 -----------　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

时间：100分钟。请同学们沉着冷静，认真答题；祝大家考出好成绩！

一．填空题（每题3分，共30分）

1．三角形的三条　　　　　　 交于一点，这点到三角形各边的距离相等；

2．一元二次方程4x²－45＝31x的二次项系数为：　　　 _　　，一次项系数为：　　 　____ ，常数项为：　　　___。

3．命题：“对顶角相等”的逆命题是　　　　　　　　　　　　 ，它是一个　　　　　　  命题。（填“真”“假”）；

4．等腰直角三角形的两边长为2和7，则它的周长为　　　　　　　  ；

5．在横线上填适当的数，使等式成立；

6．如果方程的一个根是1，那么的值是　　　 ，另一个根是　　　　；

7．三角形三边长为6、8、10，则这个三角形的面积是　　　　 。

8．在平行四边形ABCD中，对角线AC长为10，∠CAB=30°，

AB= 6，则平行四边形ABCD的面积为___________；

9．等腰梯形的上、下底分别为6、8，且有一个角为60°，则它的腰为___________；

10．等腰直角三角形斜边上的中线长为4，则其面积为　　__________；

二．选择题（每小题3分，共24分）　　　　

11．到三角形各顶点的距离相等的点是三角形　　　　　　　　　　　　　　　　  （　　）

（A）　三边的垂直平分线的交点　　　　　　　　（B）　三条高的交点　

（C）　三条角平分线的交点　　　　　　　　　　（D）　三条中线的交点

12．顺次连接四边形各边中点所得四边形一定是　　　　　　　　　　　　　　　  （　　）

（A）　平行四边形　 （B）　　 矩形　 　 （C）　　 菱形　　 （D）　　正方形

13．两条对角线垂直且相等的四边形是　　　　　　　　　　　　　　　　　　　  （　　）

（A）　　 矩形　 　　 （B）　　 菱形　　 （C）　　 正方形　（D） 以上答案均不正确

14．下列命题中，不正确的是　　　　　　　　　　　　　　　　　　　　　　　  （　　）

（A）顺次连结菱形各边中点所得的四边形是矩形　（B）有一个角是直角的菱形是正方形

（C）对角线相等且垂直的四边形是正方形（D）有一个角是60°的等腰三角形是等边三角形

15．下列方程中，为一元二次方程的是　　　　　　　　　　　　　　　　　　　  （　　）

（A）　　（B） 　 （C） （D）

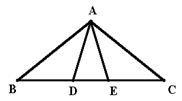16、△ABC中，AB=AC，ABC＝36，D、E是BC上的点，BAD＝DAE＝EAC，则图中等腰三角形的个数是　　　　　　　  （　　　 ）

A、2个　　B、3个　　 C、4个　　D、6个

　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　（第4题）

17．如图5，在宽为20m，长为30m的矩形地面上修建两条同样宽的道路，余下部分作为耕地. 根据图中数据，计算耕地的面积为

（A） 600m²　　　　　　（B） 551m²

（C） 550 m ²　　　 　　（D） 500m²

18．一元二次方程的根的情况是　　　　　　　　　　　　　　　　 （　　）

（A）有两个相等的实数根 （B）有两个不相等的实数根 （C） 无实数根（D）不能确定

19．用指定的方法解方程：（每题6分，共24分）

（1）（因式分解法）　　　　　　 （2）（用配方法）

　　

　　

　　

（3）（用公式法）　　　　　 （4）（用合适的方法）

三．解答题：

20．（6分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件。若商场平均每天要盈利1600元，每件衬衫应降价多少元？

21、（6分）如图7，在　　 ABCD中，AM = AB, CN = CD。

求证：四边形AMCN是平行四边形.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

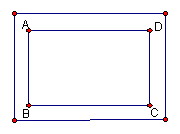22、（6分）如图，长方形ABCD，AB=20m，BC=15m，四周外围环绕着宽度相等的小路，已知小路的面积为246m²，求小路的宽度。

　　　　　

23、（6分）⑴.猜想：依次连接等腰梯形四边的中点得到的图形是一个_____　　　　  ；

⑵.证明你的猜想。(要求作出图形，写出已知、求证)

24、（9分）美化城市，改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来，

通过拆迁旧房，植草，栽树，修公园等措施，使城区绿地面积不断增加（如图）。

（1）、根据图中所提供的信息回答下列问题：2003年底的绿地面积为　　　　公顷，比2002年底增加了　　　 公顷；在2001年，2002年，2003年这三年中，绿地面积增加最多的是　　　 _年；

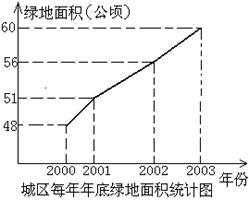（2）为满足城市发展的需要，计划到2005年底使城区绿地面积达到72.6公顷，试求今明两年绿地面积的年平均增长率。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (第26题)

25．（9分）已知：如图，在⊿ABC中，AB＝AC，ADBC，垂足为D，AN是△ABC外角CAM的平分线，CEAN，垂足为E，连接DE交AC于F。

（1）求证：四边形ADCE为矩形；（4分）

　　（2）求证：DF∥AB，DF＝AB；（4分）

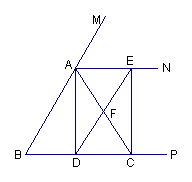（3）当⊿ABC满足什么条件时，四边形ADCE是一个正方形？简述你的理由。（3分）

北师大九年级上数学期中考试卷1参考答案

一．

1．内角平分线； 2．9、4、－31、－14； 3．相等的角是对顶角，假；

4．； 5．，；  6．，；  7．24； 8．； 9．； 10．；

二．

11．A； 12．A； 13．D； 14．C； 15．D； 16．C； 17．B； 18．B；

三．

19．（1），；（2），；（3），；

（4），；

20．解：设每件衬衫应降价元，则有

　　　　

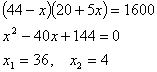
答：若商场平均每天要盈利1600元，每件衬衫应降36元或4元。但为了尽快减少库存，所以每件衬衫应降36元；

21、证明：∵ ABCD是平行四边形

　　　　  ∴ AB=CD，∠ABC=∠CDA

∵ AM = AB, CN = CD

∴ AM=CN

又∵ AB∥CD

∴ AM∥CN

∴四边形AMCN是平行四边形。

22、解：设小路的宽为xm，依题意，得

　　　　2（20x+2x）+2×15x=246

40x+4x²+30x=246

4x²=70x－246=0

 解得x₁=3，

x₂=－（不合题意，舍去）。

答：小路的宽为3m。

23．正方形：　先证四方形是平行四边形；再证明其邻边相等。

24、60、4、2002、

∵设平均增长率为x, 则60（1+x）²＝72.6

 ∴ x₁＝0.1， x₂＝－2.1（不合题意，舍去）

答：今明两年绿地面积的年增长率为10％。

25．（1）由CE⊥AN得一个直角，由∠MAC和∠BAC的角平分线互相垂直得另一个直角，再证AN∥BP后同旁内角互补得第三个直角，有三个角是直角的四边形是矩形；另证合理也给分；（2）由矩形对角线互相平分得F为AC的中点，由AD⊥BC，⊿ABC是等腰三角形，得D为BC的中点，可知ED是⊿CAB的中位线，三角形的中位线平行于第三边且等于第三边的一半；（3）⊿ABC是等腰直角三角形时满足条件。证明略；