中考数学模拟试卷(三)
班级________姓名___________号数________成绩_________等级__________
一、填空题(本题有12小题,每题3分,共36分)
1、![]() =___________。
=___________。
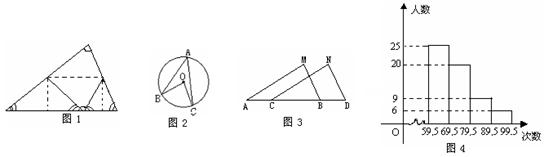
2、亲爱的同学们,在我们的生活中处处有数学的身影,请看图1,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于______________。”
3、分解因式:x2-4x+4=________________。
4、抛掷一枚六个面分别标有1、2、4、4、4、5的数字的均匀骰子,骰子停止转动后朝上的点数正好是4的概率是___________。
5、把函数y=x2-2x+3化为y=a(x-h)2+k的形式为 __________。
6、梯形上底长为6,中位线长为8,则下底长是_______________。
![]() 7、科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为153cm,下肢长为92 cm,该女士穿的高跟鞋鞋跟的最佳高度约为____________cm.(精确到O.1 cm)
7、科学研究表明,当人的下肢长与身高之比为0.618时,看起来最美.某成年女士身高为153cm,下肢长为92 cm,该女士穿的高跟鞋鞋跟的最佳高度约为____________cm.(精确到O.1 cm)
8、反比例 函数的图象经过点(3,a),则a=_________。
9、如图2,A、B、C是⊙O上的三点,∠BAC=30°,则∠BOC=_____________
10、如图3,已知MB=ND,∠MBA=∠NDC,欲使△ABM≌△CDN,还需添加的一个条件是_________________(填上一个满足题意的即可)。
11、如图4是某学校九(2)班同学的一次体检中每分钟心跳次数的频率分布直方图(次数均为正整数),则第2小组的频率为______________。
12、观察下列数表:
1 2 3 4 … 第一行
2 3 4 5 … 第二行
3 4 5 6 … 第三行
![]()
![]()
![]()
![]() 4
5
6
7 … 第四行
4
5
6
7 … 第四行
根据数表所反映的规律,第n行第n列交叉点上的数应为_____________。
二、选择题(本题有6小题,每题4分,共24分,每小题只有一个正确的答案.请把正确答案的字母代号填在括号内)
13、2004年泉州市国内生产总值已达到160 300 000 000元,用科学记数法可表示为( )
A、1.603×1010元 B、1.603×1011元
C、16 .03×1010元 D、16.03×1011元
14、观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )

15、下列调查方式合适的是( )
A、为了了解炮弹的杀伤力,采用普查的方式
B、为了了解全国中学生的睡眠状况,采用普查的方式
C、为了了解人们保护水资源的意识,采用抽样调查的方式
D、对载人航天器“神舟五号”零部件的检查,采用抽样调查的方式
16、下面是六届奥运会中国获得金牌的一览表.
| 第23届 洛杉矶奥运会 | 第24届 汉城奥运会 | 第25届 巴塞罗那奥运会 | 第26届 亚特兰大奥运会 | 第27届 悉尼奥运会 | 第28届 雅典奥运会 |
| 15块 | 5块 | 16块 | 16块 | 28块 | 32块 |
 在15、5、16、16、28、32这组数据中,众数和中位数分别是( )
在15、5、16、16、28、32这组数据中,众数和中位数分别是( )
A、16,16 B、16,15.5 C、32,16 D、16,22
17、小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同
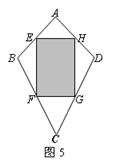
的布料生产一批形状如图5所示的风筝,点E,F,G,H分别
是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分
用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需
要甲布料30匹,那么需要乙布料( )
A.15匹 B.20匹 C.30匹 D.60匹
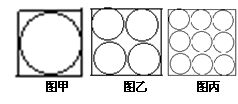 18、如图,在三个同样大小的正方形中,分别画一个内切圆,面积为S1(图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为S4(图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为S9(图丙所示);则S1 、S4和S9的大小关系是( )
18、如图,在三个同样大小的正方形中,分别画一个内切圆,面积为S1(图甲所示);画四个半径相等的两两外切、且与正方形各边都相切的圆,这四个圆的面积之和为S4(图乙所示);画九个半径相等相互外切、且与正方形各边都相切的圆,这九个圆的面积之和为S9(图丙所示);则S1 、S4和S9的大小关系是( )
(A)S1最大 (B)S4最大
(C)S9最大 (D)一样大
 三、解答题(本大题共8小题,满分70分,解答应写出文字说明、证明过程或推演步骤.)
三、解答题(本大题共8小题,满分70分,解答应写出文字说明、证明过程或推演步骤.)
19、(8分)解不等式组:
![]()
20、(8分)先化简,再求值:
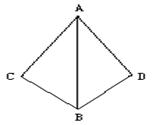 21、(8分)如图, 已知:AB平分∠CAD,AC=AD.
21、(8分)如图, 已知:AB平分∠CAD,AC=AD.
求证:BC=BD.
22、同时转动如图所示的甲、乙两个转盘,求两个转盘所转到的两个数字之和
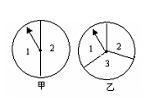 为奇数的概率(用树状图或列表法分析求解).
为奇数的概率(用树状图或列表法分析求解).
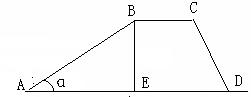 23、(8分)如图拦水坝的横断面为梯形ABCD,坡角α=320,斜坡AB=45m,求拦水坝的高BE(精确到0.01米).
23、(8分)如图拦水坝的横断面为梯形ABCD,坡角α=320,斜坡AB=45m,求拦水坝的高BE(精确到0.01米).
24、 (8分)青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
| 分组 | 频数 | 频率 |
| 3.95~4.25 | 2 | 0.04 |
| 4.25~4.55 | 8 | 0.16 |
| 4.55~4.85 | 0.40 | |
| 4.85~5.15 | 16 | 0.32 |
| 5.15~5.45 | 4 | 0.08 |
| 合计 | 1 |
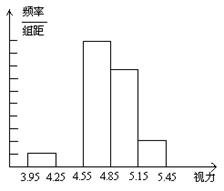
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
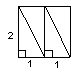 25、如图,把边长为
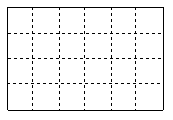
25、如图,把边长为![]() 的正方形剪成四个全等的直角三角形。
的正方形剪成四个全等的直角三角形。
请用这四个直角三角形拼成符合下列要求的图形(全部用上,
互不重叠且不留空隙),并把你的拼法仿照图中实际大小画
在方格纸内(方格为![]() )
)
(1)不是正方形的菱形(一个) (2)不是正方形的矩形(一个)

(3)梯形(一个)边形(一个) (4)不是矩形和菱形的平行四
 | |||
 | |||
(5)不是梯形和平行四边形的凸四边形(一个)
 |
![]() 26、(8分)如图,抛物线
过点A(4,0),O为坐标原点,
26、(8分)如图,抛物线
过点A(4,0),O为坐标原点,
Q是抛物线的顶点.
(1)求![]() 的值;
的值;
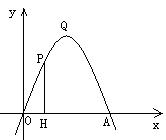 (2)点P是
(2)点P是![]() 轴上方抛物线上的一个动点,过P作PH⊥
轴上方抛物线上的一个动点,过P作PH⊥![]() 轴,H为垂足.有一个同学说:“在
轴,H为垂足.有一个同学说:“在![]() 轴上方抛物线上的所有点中,抛物线的顶点Q与
轴上方抛物线上的所有点中,抛物线的顶点Q与![]() 轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
轴相距最远,所以当点P运动至点Q时,折线P-H-O的长度最长”,请你用所学知识判断:这个同学的说法是否正确.
27、如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米,点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
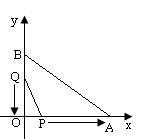 (2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似?
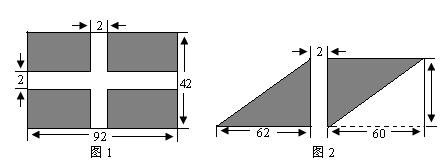
28、为了美化校园环境,争创绿色学校,某县教育局委托园林公司对A、B两校进行校园绿化。已知A校有如图1的阴影部分空地需铺设草坪。在甲、乙两地分别有同种草皮3500米2和2500米2出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
路程、运费单价表
| A校 | B校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 20 | 0.15 | 10 | 0.15 |
| 乙地 | 15 | 0.20 | 20 | 0.20 |
(注:运费单价表示每平方米草皮运送1千米所需的人民币)
求:(1)分别求出图1、图2的阴影部分面积;
(2)请你给出一种草皮运送方案,并求出总运费;
 (3)请设计总运费最省的草皮运送方案,并说明理由。
(3)请设计总运费最省的草皮运送方案,并说明理由。
