初三数学综合测试卷(2004.5)
说明:1、全卷3大题,共6页,考试时间90分钟,满分100分。
2、答题前,请在监考老师的指导下,填好试卷密封线内的姓名、校名,姓名、校名不得写在密封线以外,不得在试卷上作任何标记。
3、答选择题时,请将选项的字母代号填在答题表一内,答填空题时,请将答案填在答题表二内,做解答题时,请将解答过程写在指定的位置上。
|
每题有4个选择答案,其中只有一个是正确的,请把你认为正确答案的字母代号选填在上面的答题表一内,否则不计分。
1、下列运算正确的是( )
A、x3+x3=2x6 B、x6÷x2=x3
C、(-3x3)2=3x6 D、x2·x-3=x-1
2、若a>0,b<-2,则点(a,b+2)应在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
| 篮球编号 | 1 | 2 | 3 | 4 | 5 |
| 与标准质量的差(克) | +4 | +7 | -3 | -8 | +9 |
3、检查5个篮球的质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检查结果如下表:
质量最大的篮球比质量最小的篮球重( )
A、12克 B、15克 C、17克 D、19克
4、香港于1997年7月1日成为中华人民共和国的一个特别行政区,它的区徽图案(紫荆花)如图1,这个图形( )
 A、是轴对称图形 B、是中心对称图形
A、是轴对称图形 B、是中心对称图形
C、既是轴对称图形,也是中心对称图形
D、既不是轴对称图形,也不是中心对称图形
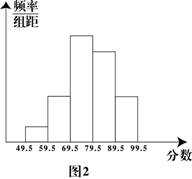 5、下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是(
)
5、下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是(
)
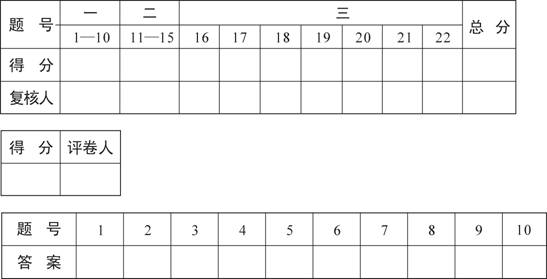
 6、某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,现将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图(如图2),已
6、某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,现将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图(如图2),已
知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.
那么在这次评比中被评为优秀的调查报告有( )
A、27篇 B、21篇 C、18篇 D、9篇
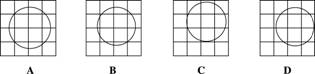
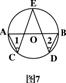
 7、如图3所示,S、R、Q在AP上,B,C,D,E在AF上,其中BS,CR,DQ,EP皆垂直于AF,且AB=BC=CD=DE,若PE=2m,则BS+CR+DQ的长是( )
7、如图3所示,S、R、Q在AP上,B,C,D,E在AF上,其中BS,CR,DQ,EP皆垂直于AF,且AB=BC=CD=DE,若PE=2m,则BS+CR+DQ的长是( )
A、![]() m B、2m C、
m B、2m C、![]() m D、3m
m D、3m
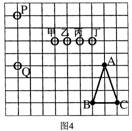
8、如图4所示,棋盘上有A、B、C三个黑子与P、Q两个
白子,要使△ABC∽△RPQ,则第三个白子R应放的位
 置可以是(
)
置可以是(
)
A、甲 B、乙 C、丙 D、丁
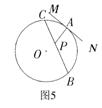
9、如图5,MN为⊙O的切线,A为切点,过A点作AP⊥MN,交⊙O的弦BC于点P,若PA=2cm,PB=5cm,PC=3cm,那么⊙O的直径等于( )
A、9cm B、![]() cm C、15cm D、
cm C、15cm D、![]() cm
cm
10、在平面直角坐标系中,若一个点的横坐标与纵坐标互为相反数,则该点一定不在( )
A、直线y=x上 B、直线y=-x上C、抛物线y=x2上 D、双曲线y=![]() 上
上
 二、填空题(本题有5小题,每题3分,共15分)请把答案填在答题表二内相应的题号下,否则不计分。
二、填空题(本题有5小题,每题3分,共15分)请把答案填在答题表二内相应的题号下,否则不计分。
|
 11、一粒纽扣式电池能够污染60升水,某市每年报废的纽扣式电池有近粒,如果废旧电池不回收,一年报废的纽扣式电池所污染的水约
升.(用科学记数法表示).
11、一粒纽扣式电池能够污染60升水,某市每年报废的纽扣式电池有近粒,如果废旧电池不回收,一年报废的纽扣式电池所污染的水约
升.(用科学记数法表示).
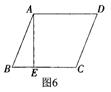
12、如图6,在菱形ABCD中,AE⊥BC于E,EC=1,cos∠B=![]() ,
,
 则这个菱形的面积是
.
则这个菱形的面积是
.
13、如图7,AB是⊙O的直径,C、D、E都是⊙O上的点,
则∠1+∠2= .
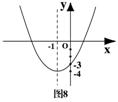
14、二次函数y=x2+bx+c的图象如图8所示,则函数值
 y<0时,对应x的取值范围是
.
y<0时,对应x的取值范围是
.
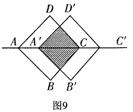
15、把正方形ABCD沿对角线AC的方向移动到正方形A′B′C′D′的位置,它们的重叠部分(图9中的阴影部分)的面积是正方形ABCD面积的一半,若AC=![]() ,则正方形移动的距离A′A的长是
.
,则正方形移动的距离A′A的长是
.
三、解答题(本部分共7题,其中第16、17题每题6分,第18、19、20、21题每题8分,第22题11分,共55分)
 16、计算:
16、计算:![]()
解:原式=
 17、解方程组
17、解方程组 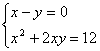
解:
 |
18、关于x的方程kx2+(k+1)x+![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围.
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出
k的值;若不存在,说明理由.
解:
 |
19、已知:如图10,在Rt△ABC中,∠ACB=90°,
AC=BC,D为BC的中点,CE⊥AD于E,BF∥AC
交CE的延长线于F.求证:AB垂直平分DF.
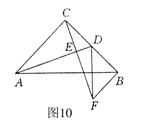 证明:
证明:
 |
20、商场销售某种商品,一月份销售了若干件,共获利润30000元,二月份把这种商品的单价降低了0.4元,但
销售量比一月份增加了5000件,从而获得的利润比一月份多2000元,求调价前每件商品的利润是多少元?
解:
 |
21、下表是小明同学填写实习报告的部分内容:
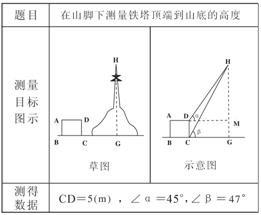
已知:sin47°=0.7313,cos47°=0.6820,tan47°=1.072,cot47°=0.9325,请你根据以上的条件,计算出铁塔顶端到山底的高度HG(结果保留两位小数).
解:

22、已知抛物线![]()
![]() 与
与![]() 轴交于A、B两
点,点A在
轴交于A、B两
点,点A在![]() 轴的负半轴上,点B在
轴的负半轴上,点B在![]() 轴的正半轴上,又此抛物线交
轴的正半轴上,又此抛物线交![]() 轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S△OAC-S△OBC=OA·OB).
轴于点C,连AC、BC,且满足△OAC的面积与△OBC的面积之差等于两线段OA与OB的积(即S△OAC-S△OBC=OA·OB).
(1)求![]() 的值;
的值;
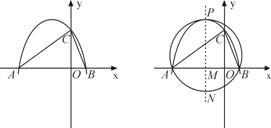 (2)若tan∠CAB=
(2)若tan∠CAB=![]() ,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为
,抛物线的顶点为点P,是否存在这样的抛物线,使得△PAB的外接圆半径为![]() ?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
解:
初三数学综合测试评分参考(2004.5)
一、选择题(每小题3分,满分共30分)
1、D 2、D 3、C 4、D 5、A 6、A 7、D 8、D 9、B 10、D
二、填空题(每小题3分,满分共15分)
11、6×108; 12、![]() 13、90o 14、
13、90o 14、![]() 15、
15、![]()
三、解答题
16、原式![]() 3分
3分
=5 6分
![]()
![]() 17、解:
17、解: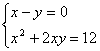
由①得![]() 代入②得
代入②得
![]() 2分
2分
即 ![]()
![]() 4分
4分
得![]()
即原方程组的解为![]() 或
或![]()
![]() 6分
6分
18、解:(1)由题意知,k≠0,且![]() 2分
2分
![]() ,且
,且![]() 4分
4分
(2)不存在 5分
设方程的两个根是![]() ,
,![]()
![]()
![]()
![]() 6分
6分
![]()
![]() ,即
,即![]()
∴满足条件的实数![]() 不存在。
8分
不存在。
8分
19、证明,∵∠ACB=90o,CE⊥AD,∴∠CAD=∠BCF 2分
又∵BF∥AC,∴∠FBC=∠DCA=90o,而AC=BC
∴△FBC≌△DCA
∴FB=CD 4分
又∵D是BC的中点,∴CD=DB
故DB=FB,即△DBF为等腰三角形 6分
又由AC=BC知 ∠CAB=∠CBA
BF∥AC知 ∠CAB=∠ABF
故∠CBA=∠ABF (说明:此处学生若从 ∠CBA=∠ABF=![]() 来论证可酌情给分 )
来论证可酌情给分 )
即AB为等腰三角形DBF的顶角平分线
∴AB垂直平分DF 8分
20、解:设调价前每件商品的利润是![]() 元
元
依题意得:![]() 3分
3分
整理得:![]()
![]()
![]()
![]() 5分
5分
经检验 ![]() ,
,![]() 均为方程的根
均为方程的根
![]() 不合题意,舍去
7分
不合题意,舍去
7分
答:调价前每件商品的利润为2元 8分
21、解:测得三个数据:DC=5m,∠α=45°,∠β=47°
设![]() 1分
1分
在Rt△CHG中
![]() 3分
3分
在Rt△DHM中
![]() ,
,
∵ ![]()
∴
![]() 5分
5分
![]() 6分
6分
![]()
![]()
答:铁塔顶端到山底的高为![]() 8分
8分
22、解:(1)设![]() 、
、![]() ,由题设可求得C点的坐标为(0,c),且
,由题设可求得C点的坐标为(0,c),且![]() ,
,
![]() 由S△AOC- S△BOC=OA·OB得:
由S△AOC- S△BOC=OA·OB得:
![]() 2分
2分
得:![]() 3分
3分
得:b=–2 4分
(2)设抛物线的对称轴与![]() 轴交于点M,与△PAB的外接圆交于点N。
轴交于点M,与△PAB的外接圆交于点N。
![]() ∵tan∠CAB=
∵tan∠CAB=![]() ,
,
∴OA=2·OC=2c, ∴A点的坐标为(-2c,0) 5分
∵A点在抛物线上,∴![]() 6分
6分
又![]() 、
、![]() 为方程
为方程![]() 的两根,
的两根,
∴![]() ,即:
,即:![]()
![]() 7分
7分
∴B点的坐标为(![]() ,0)
,0)
∴顶点P的坐标为(-![]() ,
,![]() )
8分
)
8分
由相交弦定理得:AM.BM=PM.MN
又∵![]()
∴AM=BM=![]() ,
,![]()
∴![]() 10分
10分
∴![]() ,
,![]()
∴所求抛物线的函数解析式是:![]() 11分
11分