顺德华侨中学2006年第二次月考试题
数 学 科 试 卷
亲爱的同学,这份试卷将再次记录你的自信、沉着、智慧和收获. 教师一直投给你信任的目光.请认真审题,看清要求,仔细答题,祝你考出好成绩。
说明:本试卷分为第Ι卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,满分130分,
考试时间90分钟.
第Ι卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的).
1.-3的相反数是
A.-3 B.![]() C.
C.![]() D.3
D.3
2.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是

3.粤海铁路是我国第一条横跨海峡的铁路通道,设计年输送货物能力为吨,用科学记数法应记为
A.11×106吨 B.1.1×107吨 C.11×107吨 D.1.1×108吨
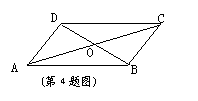 4. 如图,
4. 如图,![]() ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是
ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是
A.1<m<11 B.2<m<22
C.10<m<12 D.5<m<6
5.函数![]() 自变量
自变量![]() 的取值范围是
的取值范围是
A.x>2 B.x≥2 C.x>-2 D.x≥-2
6. 从一幅扑克牌中抽出5张红桃,4张梅花,3张黑桃放在一起洗匀后,从中一次随机抽出10张,恰好红桃、梅花、黑桃3种牌都抽到,这件事情
A.可能发生 B.不可能发生 C.很可能发生 D.必然发生
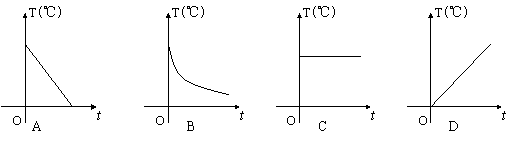
7. 夏天,一杯开水放在桌子上,杯中水的温度T(℃)随时间t变化的关系的图象是
8.一批完全相同的正多边形木板铺地面,要求顶点聚在一起,且木板之间没有缝隙,下列木板不符合要求的是
A、正三角形木板 B、正方形木板 C、正五边形木板 D、 正六边形木板
9.一张桌子上摆放着若干个碟子,从三个方向上看,三种视图如下图,则这张桌上共有碟子为
 A.6个 B.9个 C.12个 D.17个
A.6个 B.9个 C.12个 D.17个
10.两个完全相同的长方体的长、宽、高分别为5cm、4cm、3cm,把它们叠放在一起组成一个新的长方体,在这些新长方体中,表面积最大是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
顺德华侨中学2006年第二次月考试题
数 学 科 试 卷
第Ⅱ卷(非选择题 共100分)
二.填空题(本大题共5小题,每小题3分,共15分.把答案填在答题卡相应位置).
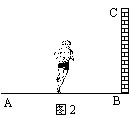 11.如图2,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而
(填“变大”、“变小”或“不变”).
11.如图2,地面A处有一支燃烧的蜡烛(长度不计),一个人在A与墙BC之间运动,则他在墙上的投影长度随着他离墙的距离变小而
(填“变大”、“变小”或“不变”).
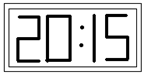
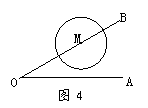
图3
12. 在平面镜里看到背后墙上,电子钟示数如图3所示,则实际时间应该是___ _
13.如图4,已知∠AOB=30°,M为OB边上一点,以M为圆心、2cm为半径作⊙M. 若点⊙M在OB边上运动,则当OM= cm时,⊙M与OA相切.
14.小明是一位刻苦学习、勤于思考、勇于创造的同学。一天,他在解方程时,突然产生了这样的想法,x2=-1这个方程在实数范围内无解,如果存在一个数i2=-1,那么方程x2=-1可以变为x2=i2,则x=+i,从而x=+i是方程x2=-1的两个根。小明还发现i具有如下性质:
i1=i;i2=-1;i3=i2×i=(-1)×i=-i;i4=(i2)2=(-1)2=1;
i5=i4×i=i;i6=(i2)3=(-1)3=-1;i7=i6×i=-i;i8=(i4)2=1……,
请你观察上述各式,根据你发现的规律填空:
i4n+1= ,i4n+2= ,i4n+3= (n为自然数)。
15. 扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出一张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆。
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 。
三.解答题(要有必要的解题步骤.16~20题各6分,21~23题各10分,24题12分,25题13分,共85分).
16. 某校在一次考试中,甲乙两班学生的数学成绩统计如下:
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲 | 1 | 6 | 12 | 11 | 15 | 5 |
| 乙 | 3 | 5 | 15 | 3 | 13 | 11 | |
请根据表格提供的信息回答下列问题:
(1) 甲班众数为______分,乙班众数为______分,从众数看成绩较好的是______班.
(2) 甲班的中位数是_______分,乙班的中位数是______分.
(3) 若成绩在85分以上为优秀,则成绩较好的是______班.
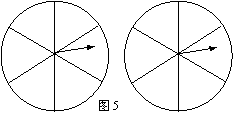
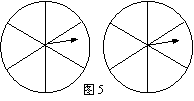 17.如图5,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(一个转盘转 出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是
17.如图5,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(一个转盘转 出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是![]() .
.
![]() 18.解不等式组
18.解不等式组 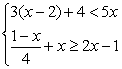 ,并把解集在数轴上表示出来。
,并把解集在数轴上表示出来。
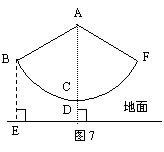
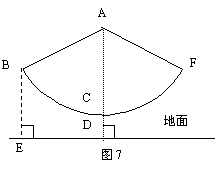
19.如图7,秋千拉绳长AB为3米,静止时踩板离
地面0.5米,某小朋友荡该秋千时,秋千在最高
处时踩板离地面2米(左右对称),请计算该秋千
所荡过的圆弧长(精确到0.1米)?
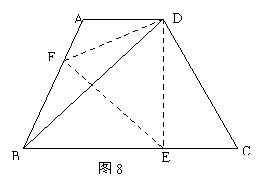
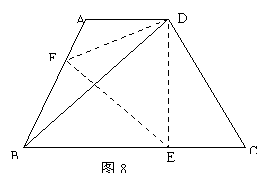 20.如图8,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交AB、BC于点F、E.若AD=2,BC=8,
20.如图8,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于点D,折痕分别交AB、BC于点F、E.若AD=2,BC=8,
求:(1)BE的长; (2)∠CDE的正切值.
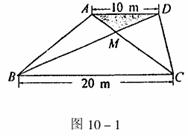
21.某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10m,20m的梯形空地上种植花木(如图10-1)
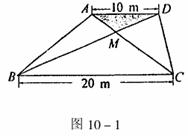 (1)他们在△AMD和BMC地带上种植太阳花,单价为8元/m2,当△AMD地带种满花后(图10-1中阴影部分),共花了160元,请计算种满△BMC地带所需的费用.
(1)他们在△AMD和BMC地带上种植太阳花,单价为8元/m2,当△AMD地带种满花后(图10-1中阴影部分),共花了160元,请计算种满△BMC地带所需的费用.
 |
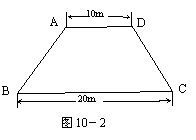
(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m2和10元/m2,应选择种哪种花木,刚好用完所筹集的资金?
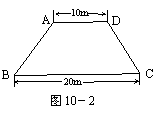
(3)若梯形ABCD为等腰梯形,面积不变(如图10-2),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC且S△APD= S△BPC,并说出你的理由.
 |
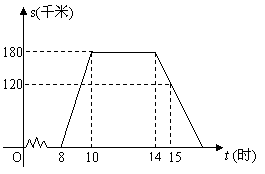
22.“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
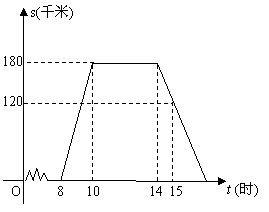 (2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(2)求出返程途中,s(千米)与时间t(时)的函数关系,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的
油箱总容量为35升,汽车每行驶1千米耗
油![]() 升.请你就“何时加油和加油量”给
升.请你就“何时加油和加油量”给
小明全家提出一个合理化的建议.
(加油所用时间忽略不计)
23.阅读:
我们知道,在数轴上,x=1表示一个点,而在平面直角坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形就是一次函数y=2x+1的图象,它也是一条直线,如图①.
观察图①可以得出:直线=1与直线y=2x+1的交点P的坐标(1,3)就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为![]()
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它左侧的部分,如图②;y≤2x+1也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图③。
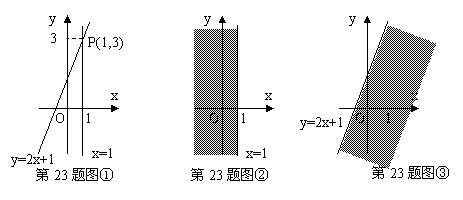 |
回答下列问题:
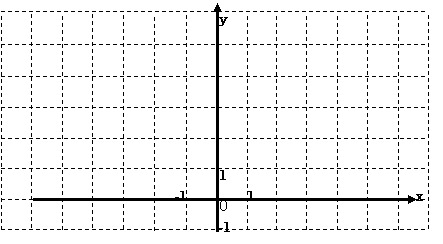
(1)
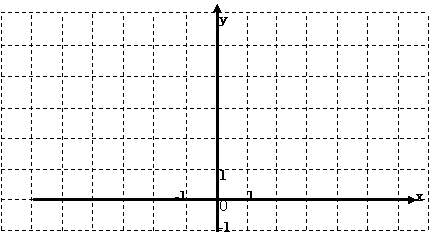
在下图的直角坐标系中,用作图象的方法求出方程组![]() 的解;
的解;
(2)
 用阴影表示
用阴影表示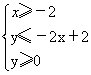 所围成的区域。并求阴影区域的面积。
所围成的区域。并求阴影区域的面积。
24.顺次连结n(n≥3,n为整数)边形各边中点所地的边形,叫做中点边形。
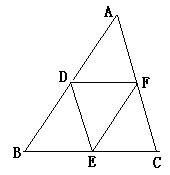
(1)
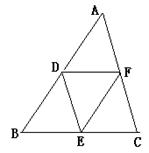
 如下图,△DEF是△ABC的中点三角形。求证:△DEF的面积是△ABC面积的四分之一;
如下图,△DEF是△ABC的中点三角形。求证:△DEF的面积是△ABC面积的四分之一;
第24图① 第24图②
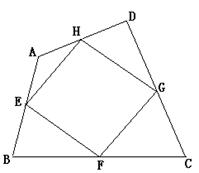
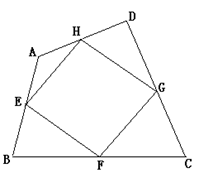
(2) 如上图,若四边形EFGH是四边形ABCD的中点四边形。
① 请判断中点四边形EFGH的形状,并加以证明。
② 探索中点四边形EFGH的面积与四边形ABCD的面积间的关系,写出探索的过程并对自己所探索的结论进行证明。
25.已知抛物线y=x2+(2n-1)x+n2-1 (n为常数).
(1)当抛物线经过坐标原点,且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由.
顺德华侨中学2006年第二次月考试题
数 学 科 试 卷 (答 题 卷)
一.选择题(本大题共10个小题,每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题(本大题共5小题,每小题3分,共15分.把答案填在答题卡相应位置).
11 ;12 ; 13 OM= cm;
14 i4n+1= ,i4n+2= ,i4n+3= (n为自然数); 15 。
三.解答题(要有必要的解题步骤.16~20题各6分,21~23题各10分,24题12分,25题13分,共85分).
16:(1) ; ; 。
(2) ; 。(3) 。
 17:解:
17:解:
 18:解:由
18:解:由 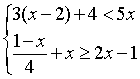
 19:解:
19:解:
 |
20;解:
 |
21:解:(1)
 (2)
(2)
(3)
 22:解:(1)
22:解:(1)
(2)
(3)
 23:解:(1)如图:
23:解:(1)如图:
(2)
 24:(1)证明:
24:(1)证明:
(2):①
②:
25:(1)
(2)
结束语:再仔细检查一下,也许你会做得更好,祝你成功!