2005年太原市初中毕业、升学数学考试
参考资料:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(―![]() ,
,![]() ),对称轴是x=―
),对称轴是x=―![]() ;
;
![]() ≈1.4,
≈1.4,![]() ≈1.7。
≈1.7。
一、选择题:(本大题含10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项符合题目要求)
1.―4的倒数是( )
A.![]() B.―
B.―![]() C.4 D.―4
C.4 D.―4
2.如图,两条直线a、b被第三条直线c所截,如果a∥b,∠1=50º,那么∠2的度数为( )
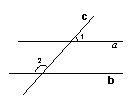 A.130º B.100º C.80º D.40º
A.130º B.100º C.80º D.40º
3.下列图形中,只有两条对称轴的是( )
A.正六边形 B.矩形 C.等腰梯形 D.圆
4.在函数y=![]() 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≥―3 B.x≠4 C.x≥―3,且x≠4 D.x≥3,且x≠4
![]() 5.实数a在数轴上的位置如图所示,化简a+1的结果是( )
5.实数a在数轴上的位置如图所示,化简a+1的结果是( )
A.a+1 B.―a+1 C.a―1 D.―a―1
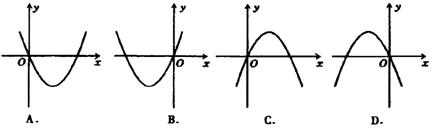 6.在反比例函数y=
6.在反比例函数y=![]() 中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( )
中,当x>0时,y随x的增大而增大,则二次函数y=kx2+2kx的图像大致是( )
7.为了解晋龙中学某班学生每天的睡眠情况,随机抽取该班10名学生,在一段时间里,每人平均每天的睡眠时间统计如下(单位:小时):6,8,8,7,7,9,10,7,6,9,由此估计该班多数学生每天的睡眠时间为( )
A.7小时 B.7.5小时 C.7.7小时 D.8小时
8.A、B、C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是( )
 A.可以画一个圆,使A、B、C都在圆上
A.可以画一个圆,使A、B、C都在圆上
B.可以画一个圆,使A、B在圆上,C在圆外
C.可以画一个圆,使A、C在圆上,B在圆外
D.可以画一个圆,使B、C在圆上,A在圆内
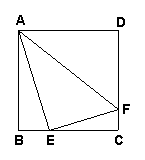
9.如图,在正方形ABCD中,点E、F分别在边BC、CD上,
如果AE=4,EF=2,AF=5,那么正方形ABCD的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.某污水处理厂的一个净化水池设有2个进水口和1个出水口,三个水口至少打开一个。每个进水口进水的速度由图甲给出,出水口出水的速度由图乙给出。某—天0点到6点,该水池的蓄水量与时间的函数关系如图丙所示。通过对图像的观察,小亮得出了以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水,(3)4点到6点不进水也不出水。其中正确的是( )
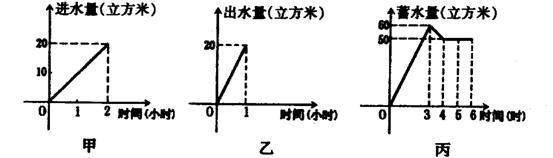
A.(1) B.(3) C.(1)(3) D.(1)(2)(3)
二、填空题:(本大题含10个小题,每小题2分,共20分。将下列各题的结果填在题中横线上)
11.在平面直角坐标系中,点(―3,4)关于y轴对称的点的坐标为______。
 12.计算2―2的结果是______。
12.计算2―2的结果是______。
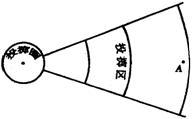
13.右图是比例尺为1∶200的铅球场地的示意图,铅球
投掷圈的直径为2.135m,体育课上,某生推出的铅球
落在投掷区的点A处,他的铅球成绩约为______m。
(精确到0.1m)
14.把3x2―6x+3分解因式,其结果是____________。
15.不解方程,判别方程2y2―8y+5=0的根的情况是____________。
16.将棱长分别为acm和bcm的两个正方体铝块熔化,制成一个大正方体铝块,这个大正方体的棱长为______cm。(不计损耗)
17.某地区开展“科技下乡”活动三年来,接受科技培训的人员累计达95万人次,其中第一年培训了20万人次。设每年接受科技培训的人次的平均增长率都为x,根据题意列出的方程是____________。
 18.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形。如(1)(2)(5)
18.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形。如(1)(2)(5)![]() ABCD是菱形,再写出符合要求的两个:________
ABCD是菱形,再写出符合要求的两个:________![]() ABCD是菱形;________
ABCD是菱形;________![]() ABCD是菱形。
ABCD是菱形。
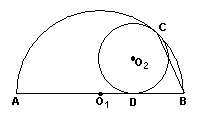
9.如图,⊙O2与半圆Ol内切于点C,与半圆的直径AB
切于点D,若AB=6,⊙O2的半径为1,则∠ABC的
度数为________。
20.如图,乐器上的一根弦AB=80cm,
两个端点A、B固定在乐器板面上,
 支撑点C是靠近点B的黄金分割点
支撑点C是靠近点B的黄金分割点
(即AC是AB与BC的比例中项),
支撑点D是靠近点A的黄金分割
点,则AC=___cm,DC=____cm。
三、解答题:(本大题含9个小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤)
21.(本小题满分7分)
解不等式组: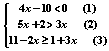
22.(本小题满分6分)
计算:![]() ÷(a―
÷(a―![]() )
)
23.(本小题满分6分)
下图显示的是今年2月25日《太原日报》刊登的太原市2002年至2004年财政总收入完成情况,图中数据精确到1亿元,根据图中数据完成下列各题:
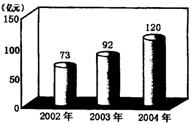 (1)2003年比2002年财政总收入增加了_______亿元;
(1)2003年比2002年财政总收入增加了_______亿元;
(2)2004年财政总收入的年增长率是_______;(精确到1%)
(3)假如2005年财政总收入的年增长率不低于2004年财政
总收入的年增长率,预计2005年财政总收入至少达到___
亿元。(精确到1亿元)
评分说明:每填对1空得2分,共6分。
24.(本小题满分7分)
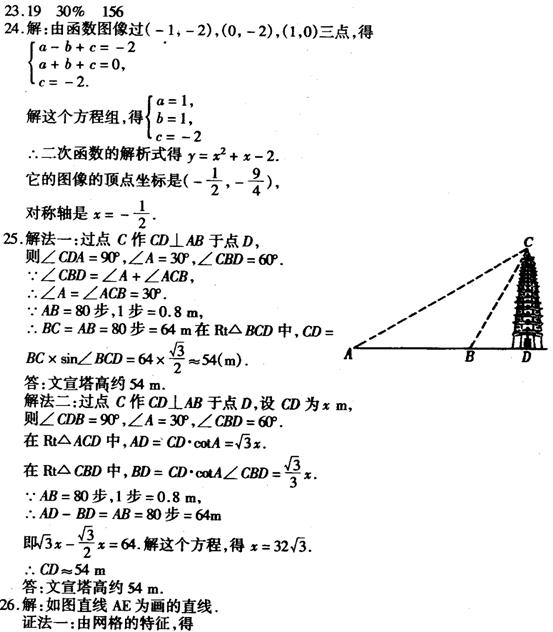
已知二次函数y=ax2+bx+c的部分对应值如下表,求这个函数的解析式,并写出其图像的顶点坐标和对称轴。
| x | ―2 | ―1 | 0 | 1 | 2 | 3 |
| y | 0 | ―2 | ―2 | 0 | 4 | 10 |
25.(本小题满分8分)
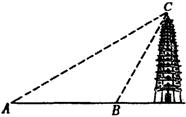 某学校宏志班的同学们五一期间去双塔寺观赏牡丹,同时对文宣塔的高度进行了测量。如图,他们先在A处测得塔顶C的仰角为30º;再向塔的方向直行80步到达B处,又测得塔顶C的仰角为60º。请用以上数据计算塔高。(学生的身高忽略不计,1步=0.8m,结果精确到1m)
某学校宏志班的同学们五一期间去双塔寺观赏牡丹,同时对文宣塔的高度进行了测量。如图,他们先在A处测得塔顶C的仰角为30º;再向塔的方向直行80步到达B处,又测得塔顶C的仰角为60º。请用以上数据计算塔高。(学生的身高忽略不计,1步=0.8m,结果精确到1m)
26.(本小题满分5分)
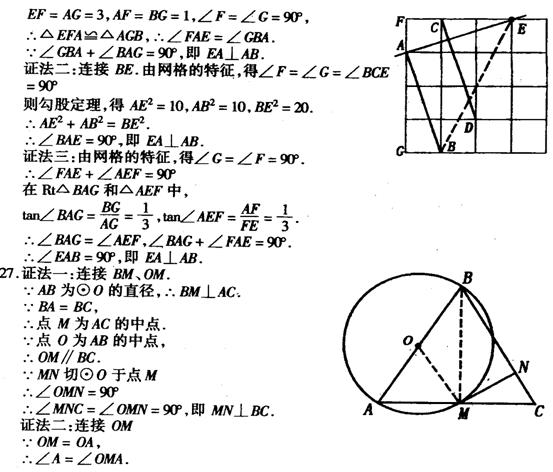
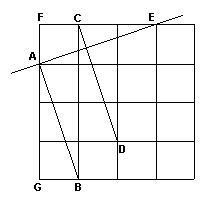 在4×4的正方形网格中,每个小方形的边长都是1。线段AB和CD分别是图中1×3的两个矩形的对角线,显然AB∥CD。请你用类似的方法画出过点E且垂直于AB的直线,并证明。
在4×4的正方形网格中,每个小方形的边长都是1。线段AB和CD分别是图中1×3的两个矩形的对角线,显然AB∥CD。请你用类似的方法画出过点E且垂直于AB的直线,并证明。
27.(本小题满分9分)
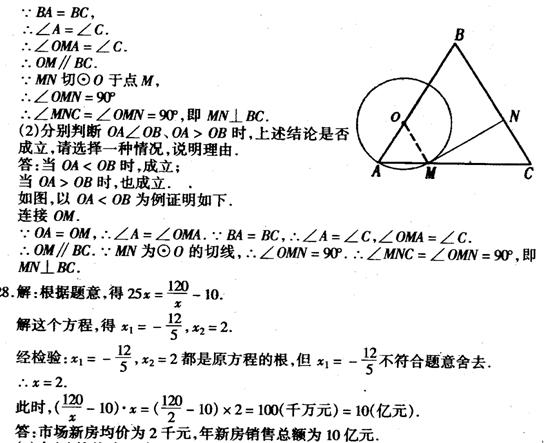
如图,在锐角△ABC中,BA=BC,点O是边AB上的一个动点(不与点A、B重合),以O为圆心,OA为半径的圆交边AC于点M,过点M作⊙O的切线MN交BC于点N。
 (1)当OA=OB时,求证:MN⊥BC;
(1)当OA=OB时,求证:MN⊥BC;
(2)分别判断OA<OB、OA>OB时,上述结论是否成立。
请选择一种情况,说明理由。
28.(本小题满分10分)
某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=![]() ―10;
―10;
(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;
(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理化的建议。(字数不超过50)
29.(本小题满分12分)
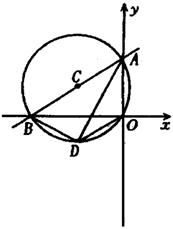
如图,直线y=![]() x+2与y轴交于点A,与x轴交于点B,⊙C是△ABO的外接圆(O为坐标原点),∠BAO的平分线交⊙C于点D,连接BD、OD。
x+2与y轴交于点A,与x轴交于点B,⊙C是△ABO的外接圆(O为坐标原点),∠BAO的平分线交⊙C于点D,连接BD、OD。
(1)求证:BD=AO;
(2)在坐标轴上求点E,使得△ODE与△OAB相似;
![]() (3)设点A′在OAB上由O向B移动,但不与点O、B重合,记△OA′B的内心为I,点I随点A′的移动所经过的路程为l,求l的取值范围。
(3)设点A′在OAB上由O向B移动,但不与点O、B重合,记△OA′B的内心为I,点I随点A′的移动所经过的路程为l,求l的取值范围。
2005年太原市初中毕业、升学数学考试答案