2006年中考全真模拟试卷（一）
| 题号 | 一 | 二 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 总分 |
| 得分 |
一、选择题（每题3分，共36分.每小题有四个选项，其中只有一个选项是正确
的，将正确选项前的字母填入下表相应的题号下面.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、 本地１月份的某一天，最高气温为７˚Ｃ，最低温度为－２˚Ｃ，则这一天的最高气温 比最低温度高
Ａ、５˚Ｃ Ｂ、９˚Ｃ Ｃ、－２˚Ｃ Ｄ、－９˚Ｃ
2、下列各式的计算结果是a6的是
A．
Ｂ．
Ｃ．
Ｄ．a2·
a3
3、若点P（1－m，m）在第二象限，则下列关系式正确的是
A．0＜m＜1 B．m＞0 C．m＞1 D．m＜0
4、学校商店销售一种练习本所获的总利润y(元)与销售单价x(元)之间的函数关系式为y＝－2(x－2)2+48，则下列叙述正确的是
A、当x＝2时，利润有最大值48元 B、当x＝－2时，利润有最大值48元
C、当x＝2时，利润有最小值48元 D、当x＝－2时，利润有最小值48元
5、下列有关概率的叙述，正确的是 ( )
(A)投掷一枚图钉，针尖朝上、朝下的概率一样
(B)投掷一枚均匀硬币，正面朝上的概率是
(C)统一发票有“中奖”与“不中奖”二种情形，所以中奖概率是
(D)投掷一枚均匀骰子，每一种点数出现的概率都是
，所以每投六次，必会出现一次“1点”
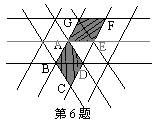
6、相信同学们都玩过万花筒，如上图是某个万花筒的造型，图中的小三角形均是全等的等边三角形，那么图中的菱形AEFG可以看成是把菱形ABCD以点A为旋转中心
A、顺时针旋转60°得到 B、顺时针旋转120°得到
C、逆时针旋转60°得到 D、逆时针旋转120°得到
7、如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC＝30°，则∠CAD等于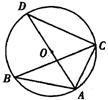
（A）30° （B）40° （C）50° （D）60°
8、已知菱形的边长为6,一个内角为600, 则菱形较短的对角线长是
A、
B、
C、3
D、6
9、已知圆柱的侧面积是10πcm2，若圆柱底面半径为r（cm），高线长为h（cm），则h关于r的函数的图象大致是
10、有十五位同学参加智力竞赛，且他们的分数互不相同，取八位同学进入决赛，某人知道了自己的分数后，还需知道这十五位同学的分数的什么量，就能判断他能不能进入决赛.
A、平均数 B、众数 C、中位数 D、最高分数
11、一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为
A、6个 B、8个 C、12个 D、17个
12、红星中学初三（6）班十几名同学毕业前和数学老师合影留念，一张彩色底片要0.6元，扩印一张相片0.5元，每人分一张，免费赠送老师一张（由学生出钱），每个学生交0.6元刚好，则相片上共有多少人?
A．13个 B．12个 C．11个 D．10个
二、填空题 (每题4分，共24分.)
13、一粒纽扣式电池能够污染60万升水，我市每年报废的纽扣式电池约400000粒，如果废旧电池不回收，我县一年报废的纽扣式电池所污染的水约有 升（用科学记数法表示）.
14、在抛掷两枚普通的正方体骰子的实验中，列举一个不可能事件：
_______________________________________________________________.
15、如图，当半径为30cm的传送带转动轮转过120°角时，传送带上的物体A平移的距离为 _____cm(保留
)。
16、用高1.5米的测角仪器CD（能测量仰角，俯角的仪器）和皮尺测量校园内旗杆的高度，其方案如图所示，则需测得的数据有： .
17、2005年4月30日通车的润扬长江大桥是我国第一座由悬索桥和斜拉桥构成的组合型特大桥梁，其北汊桥为斜拉桥，它是利用一组组钢索，把桥面重力传递到两侧的高塔上。如图，A1B1、A2B2、A3B3、A4B4是斜拉桥上4条互相平行的钢索，并且钢索的一端B1、B2、B3、B4被均匀地固定在桥上，如果钢索A2B2=70米，钢索A4B4=30米，那么钢索A1B1的长 为___________米。
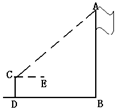
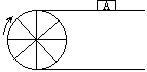
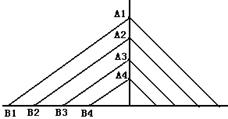
(第15题图) (第16题图) (第17题图)
18、某市出租车收费标准如下：起步价：5元；基价里程：3公里；等时费：每等5分钟加收1公里的租价； 租价：每公里1.20元. 星期天，某同学从家出发坐出租车去火车站接一朋友回家.表示该同学离家距离与离家时间的关系如图所示，则该同学最少应付车费 元.（注：1公里=1千米）
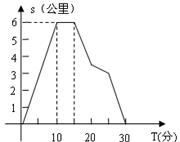
三、解答下列各题 (本大题共8题，计90分.解答时应写明演算步骤、证明过程或必要的文字说明.)
19、（本题满分8分）当
时，求代数式
的值.
20、（本题满分10分）如图, 在矩形ABCD中, 对角线AC、BD相交于点O.
⑴画出△AOB平移后的三角形, 其平移的方向为射线AD的方向, 平移的距离为线段AD的长(不写画法, 保留画图痕迹);
⑵在第⑴题画成功的图形中,
除了矩形ABCD外还有哪一种特殊的平行四边形? 并给予证明.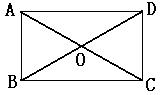
21、（本题满分10分）如图，某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品，下表是活动进行中的一组统计数据：
⑴ 计算并完成表格；
| 转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 |
⑵ 请估计当n很大时，频率将会接近多少？
⑶ 假如你去转动该转盘一次，你获得可乐的概率是多少？在该转盘中，表示“可乐”区域的扇形的圆心角约是多少度？
⑷ 如果转盘被一位小朋友不小心损坏, 请你设计一个模拟实验方案(要求交代清楚替代工具和游戏规则).
22、(本题满分12分) 三等分任意角是一个作图难题, 在距第一次提出这个问题两千年之后，这个问题才被证实用尺规作图(用没有刻度的直尺和圆规作图)无法解决. 现在有不少人创造了各种各样的辅助工具，用来解决尺规作图无法解决的三等分任意角的问题.
如图所示就是一个用来三等分任意角的工具及其使用示意图.
⑴ 制作该工具时BE所在的直线、点C应分别满足什么条件? 使用时应注意些什么?
⑵ 你能说出该工具三等分任意角的道理吗？
23、（本题满分12分）在足球比赛中，当守门员远离球门时，进攻队员常常使用“吊射”的战术（把球高高地挑过守门员的头顶，射入球门）．一位球员在离对方球门30米的M处起脚吊射，假如球飞行的路线是一条抛物线，在离球门14米时，足球达到最大高度
米。如图以球门底部为坐标原点建立坐标系，球门PQ的高度为2.44米．问：
⑴ 通过计算说明，球是否会进球门？
⑵ 如果守门员站在距离球门2米远处，而守门员跳起后最多能摸到2.75米高处，他能否在空中截住这次吊射？
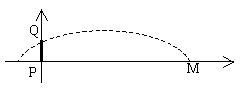
24、（本题满分12分）
图(1)是一个10×10格点正方形组成的网格. △ABC是格点三角形(顶点在网格交点处), 请你完成下面两个问题:
(1) 在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,
且△A1B1C1与△ABC的相似比是2, △A2B2C2与△ABC的相似比是
.
(2) 在图(2)中用与△ABC、△A1B1C1、△A2B2C2全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.
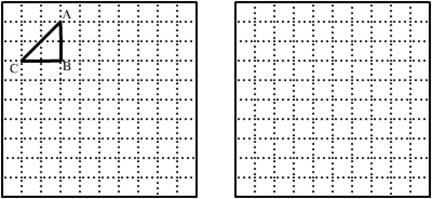
【解说词】
25、（本题满分12分）2005年4月20日发生在我市部分地区的大风冰雹灾害，使江都、宝应等县市8个乡镇、25万人受灾，当地政府已启动救灾应急预案，组织力量妥善安排受灾群众生活，各项抢险救灾工作正在紧张有序进行当中。一方有难八方支援，我市人民及时伸出了援助之手，迅速组织了一批救灾物资运往灾区。
这批物资若用n辆载重量为5吨的汽车装运，则会剩余21吨物资；若用n辆载重量为8吨的汽车装运，则有（n-1）辆汽车满载，最后一辆汽车不空，但所载物资不足5吨。⑴ 这批物资共有多少吨？
⑵ 已知载重量为5吨和8吨的汽车的租金分别为200元／辆、300元／辆, 若同时租用这两种汽车(每辆汽车都满载)共花费2600元, 则分别租用这两种汽车各多少辆?
⑶ 若同时使用载重量为5吨和8吨的两种汽车运输，请你设计一种方案，使每辆汽车都满载，且所需车辆数量最少。
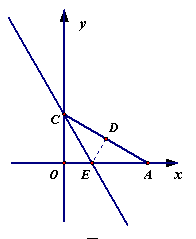
26、（本题满分14分）如图，Rt △OAC是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在x轴上，点C在y轴上，OC=
，∠CAO＝30º．将Rt △OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE.
⑴求折痕CE所在直线的解析式；
⑵求点D的坐标
⑶设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以Ｍ、Ｎ、Ｄ、Ｃ为顶点的四边形是平行四边形？若存在，请求出符合条件的点Ｍ的坐标；若不存在，请说明理由．
2006年中考全真模拟试卷（一）参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | A | B | D | D | D | B | C | C | B |
二、填空题 www.czsx.com.cn
13、2.4×1011
14、略（所举事件应在抛两枚骰子的情境下，且不应出现“不可能”等判断性词语）
15、20
16、∠ACE的度数和线段BD的长
17、90
18、17元
三、解答下列各题www.czsx.com.cn
19、原式=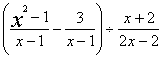
=
=
=
当x=
时
原式=
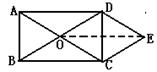
20、⑴如图见右图
⑵四边形OCED为菱形
证明：∵DE∥OC，CE∥OD ∴四边形OCED为平行四边形
∵四边形ABCD为矩形∴AC=BD，OA=OC=1/2AC，OB=OD=1/2BD
∴OC=OD （2分）
∵四边形OCED为平行四边形 且OC=OD
∴四边形OCED为菱形
21、⑴68%，74%，78%，69%，70.5%,70.1%
⑵当n很大时，频率将会接近70%
⑶获得可乐的概率为30%，圆心角约为360º×30%=108º
⑷模拟实验方案：在一不透明口袋内放置红球3个、蓝球7个，搅均后从中随机摸出一个球，摸出红球获得可乐，摸出蓝球获得铅笔. （本方案仅供参考,其他方案酌情加分）
22、⑴直线BE垂直平分线段AC；C为BD中点（或C为半圆圆心）,点A放在角的一边上，角的另一边与半圆相切，BE经过角的顶点.
⑵∵BE垂直平分AC ∴EA=EC
∵EA=EC且EB⊥AC ∴∠AEB=∠BEC
∵EF为半圆切线 ∴CF⊥EF
∵CB⊥EB，CF⊥EF且CB=CF
∴∠BEC=∠CEF
∴∠AEB=∠BEC=∠CEF
23、⑴设抛物线解析式为y=a(x-14)2+32/3
∵经过点M（30，0） ∴a=-1/24
∴y=-1/24（x-14）2+32/3
当x=0时y=5/2
∵y=2.5>2.44
∴球不会进球门
⑵当x=2时，y=14/3
∵y=14/3＞2.75
∴守门员不能在空中截住这次吊射.
24、图形不唯一，符合要求即可.
25、⑴5n+21-8(n-1)>0 5n+21-8(n-1)<5
解得8<n<29/3
∵n为整数 ∴n=9
∴物资总吨数=5×9+21=66吨
⑵设载重量5吨的汽车辆数为x, 载重量8吨的汽车辆数为y, 则
5x+8y=66, 200x+300y=2600
解得 x=10 y=2 ∴载重量5吨的汽车10辆, 载重量8吨的汽车2辆.
⑶设汽车总辆数为y，载重量5吨的汽车辆数为x（x≥0）
则y=x+(66-5x)/8=(3x+66)/8
由函数解析式知当x最小且使3x+66为8的倍数时y最小
∴当x最小=2时y最小=9
26、(1) 
(2) D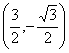
(3) 符合条件的点Ｍ存在,
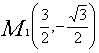或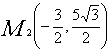
.www.czsx.com.cn