初三期末试题
（总分120分，时间120分钟）
一、选择题：（本大题共10小题,每小题3分,共30分）
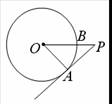1.如右图，PA为⊙O的切线，A为切点，PO交⊙O于点B，PA=4，OA=3，
则cos∠APO的值为（ ）
A．
B．
C．
D．
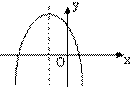2．已知二次函数
的图象如右图所示，
ａ、ｂ、ｃ满足（ ）
Ａ．a＜0,b＜0,c＞0 B. a＜0,b＜0, c＜0
C．a＜0,b＞0,c＞0 D. a＞0,b＜0,c＞0
3．Rt△ABC中，∠Ｃ＝90°,AC=3cm,BC=4cm.给出下列三个结论:
① 以点C为圆心,2.3cm长为半径的圆与AB相离;
② 以点C为圆心,2.4cm长为半径的圆与AB相切;
③ 以点C为圆心,2.5cm长为半径的圆与AB相交;则上述结论中正确的个数是（ ）
A.0个 B.1个 C.2个 D.3个
4.若半径为2cm和3cm的两圆相外切,那么与这两个圆都相切且半径为5cm的圆的个数是（ ）
A.5个 B.4个 C.3个 D.2个
5.已知抛物线
，图象与y轴交点的坐标是（ ）
A．（0，3） B.（0，-3） C.（0，
） D.（0， -）
6．以正方形ABCD的顶点A为圆心，AB长为半径画⊙A，则经过B、D两点的直线和⊙A的位置关系（ ）
（A）相离 （B）相切
（C）相交 （D）不能确定
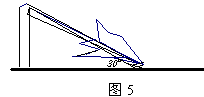7.如图5，一棵大树在一次强台风中于离地面5米处折断倒下，
倒下部分与地面成30°夹角，这棵大树在折断前的高度为（ ）
A．10米 B．15米 C．25米 D．30米
8．在通常情况下，地面到10km高空的范围内，从地面开始高度每 增 加1km，气温就下降一定的数值．如下表所示，能表示通过测量得到的气温y（℃）与增加的高度x（km）之间关系的式子（不考虑自变量x的取值范围）是
| 增加的高度x（km） | 2 | 4 | 5 | 8 | 9 | 10 |
| 气温y（℃） | 2 | －11 | －17.5 | －37 | －43.5 | －50 |
（A）
（B）
（C）y＝x （D）
9.下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ）
 |
A. 1个 B. 2个 C . 3个 D. 4个
10、如图，点P按A→B→C→M的顺序在边长为1的正方形边上运动，M是CD边上的中点.
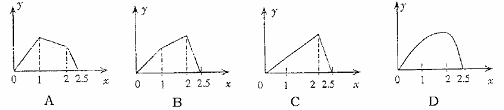
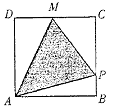设点P经过的路程x为自变量，△APM的面积为y，则函数y的大致图像是（）
二、填空题（本大题共10小题，每小题3分，共30分）
11．如图11，在⊙O中，已知∠ACB=∠CDB=60°，AC=3，则△ABC的周长是 ．
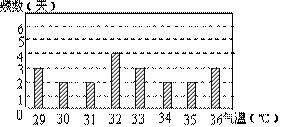
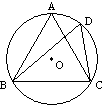
图11 图12
12．根据某市去年7月份中某21天的各天最高气温（℃）记录，制作了如图的统计图12，由图中信息可知，，其中最高气温的中位数是 ℃，
13. 用48米长的竹篱笆在空地上,围成一个绿化场地,现有两种设计方案,一种是围成正方形的场地;另一种是围成圆形场地.现请你选择,围成________(圆形、正方形两者选一)场在面积较大.
14．
如图，已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后，点D落在CB的延长线上的D′点处,那么
′等于__________.
15．在RtΔABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，CA为半径的圆与AB、BC分别交于点D、E，则.AD=_______．
16. 在直径为10m的圆柱形油槽内装入一些油后，截面如图16所示，如果油面宽AB=8m，
那么油的最大深度是______m.
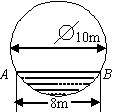
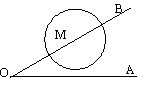
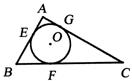
图16 图18 图17
17．如图17，已知∠AOB = 30 ，M为OB边上一点，以M为圆心、2cm为半径作⊙M.若点M在OB边上运动，则当OM= cm时，⊙M与OA相切.
18．如图18，⊙O是△ABC的内切圆，切点分别为E、F、G，若GC＝10，BF＝3，AG＝2，则△ABC为________三角形．
19．已知抛物线
的顶点坐标为（2，3），则
的根是
。
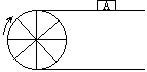20、如右图，当半径为30cm的转动轮转过120°角时，
传送带上的物体A平移的距离为 cm。
三、解答题（本大题共4小题，每小题6分，共24分）
21.圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
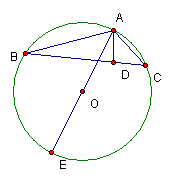
22．已知如图，在△ABC中，AB=6，AC=3，BC边上的高AD=2，
⊙O经过A，B，C三点，求⊙O的直径AE的长。
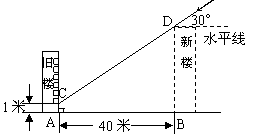
23、为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为40米，中午12时不能挡光.如图，某旧楼的一楼窗台高1米，要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射，并且光线与水平线的夹角最小为30°，在不违反规定的情况下，请问新建楼房最高多少米？（结果精确到1米.
，
）
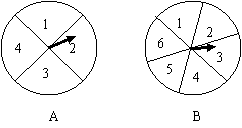
24、如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字。有人为甲乙两人设计了一个游戏，其规则如下：
（1） 同时转动转盘A与B；
（2） 转盘停止后，指针各指向一个数字（如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止），用所指的两个数字作乘积，如果所得的积是偶数，那么甲得1分；如果所得的积是奇数，那么乙得1分。
你认为这样的规则是否公平？请你说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
四．本题8分
25．已知：二次函数的图象经过点A（－1，0），B（0，－3），对称轴方程为x＝1．
（1）求此二次函数的解析式；
（2）若以坐标原点O为圆心，4为半径作圆，判断点顶点P与⊙O的位置关系．
五．本题8分
26．如示意图所示，边长为2的等边△ABC是三棱镜的一个横截面，一束光线沿着与AB边垂直的方向射入到BC边上的D点处（D点与B、C两点不重合），反射光线又从AC边射出去．DK为法线．设BE的长为x，AF的长为y．
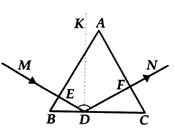（1）求y和x之间的函数关系式，并写出自变量x的取值范围；
（2）画出该函数的图象．
六．本题10分
27如图16，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．
E为BC的中点，以OE为直径的⊙O′交
轴于D点，过点D作DF⊥AE于点F．
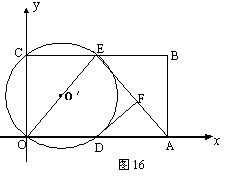(1) 求OA、OC的长；
解：
(2) 求证：DF为⊙O′的切线；
证明：
(3) 小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．
七．本题10分
28.某广告公司设计一幅周长为12 m的矩形广告牌，广告设计费为每平方米1000元.设矩形一边长为x cm，面积为S cm2.
(1)求出S与x之间的函数关系式，并确定自变量x的取值范围;
(2)请你设计一个方案，使获得的设计费最多，并求出这个费用;
(3)为使广告牌美观、大方，要求做成黄金矩形，请你设计出符合要求的方案，并计算可获得多少元的设计费.(精确到元)〔参考资料：①当矩形的长是宽与(长+宽)的比例中项时，这样的矩形叫黄金矩形；②
≈2.236〕