2005年杭州地区中考数学压轴题精选
(2005杭州)25.(本小题满分10分)
 为了参加市科技节展览,同学们制造了一
为了参加市科技节展览,同学们制造了一
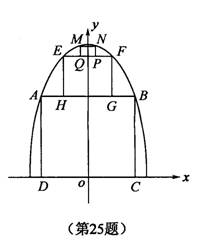
个截面为抛物线形的隧道模型,用了三种正方
形的钢筋支架.在画设计图时,如果在直角坐
标系中,抛物线的函数解析式为![]() ,
,
正方形ABCD的边长和正方形EFGH的边长
之比为5:1,求:
(1)抛物线解析式中常数![]() 的值;
的值;
(2)正方形MNPQ的边长.
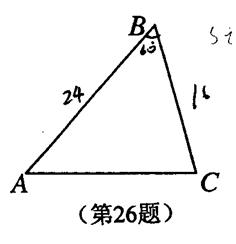 26.(本小题满分12分)在三角形ABC中,
26.(本小题满分12分)在三角形ABC中, ![]() .现有动点P从点A出发,沿射线AB向点B方向运动;动点Q从点C出发,沿射线CB也向点B方向运动.如果点P的速度是
.现有动点P从点A出发,沿射线AB向点B方向运动;动点Q从点C出发,沿射线CB也向点B方向运动.如果点P的速度是![]() /秒,点Q的速度是
/秒,点Q的速度是![]() /秒,它们同时出发,求:
/秒,它们同时出发,求:
(1)几秒钟后,ΔPBQ的面积是ΔABC的面积的一半?
(2)在第(1)问的前提下,P,Q两点之间的距离是多少?
(2005金华)24、(本题12分)
如图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=![]() ,过D,E两点作直线PQ,与BC边所在的直线MN相交于点F。
,过D,E两点作直线PQ,与BC边所在的直线MN相交于点F。
(1)求tan∠ADE的值;
(2)点G是线段AD上的一个动点(不运动至点A,D),GH⊥DE垂足为H,设DG为x,四边形AEHG的面积为y,请求出y与x之间的函数关系式;
(3)
 |
如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切。问满足条件的⊙O有几个?并求出其中一个圆的半径。
25(本题14分)
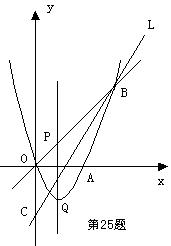
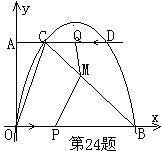
如图,抛物线![]() 经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线
经过点O(0,0),A(4,0),B(5,5),点C是y轴负半轴上一点,直线![]() 经过B,C两点,且
经过B,C两点,且![]()
(1)求抛物线的解析式;
(2)求直线![]() 的解析式;
的解析式;
(3)过O,B两点作直线,如果P是直线OB上的一个动点,过点P作直线PQ平行于y轴,交抛物线于点Q。问:是否存在点P,使得以P,Q,B为顶点的三角形与
△OBC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由。
 |
(2005绍兴)24.(本题满分12分)
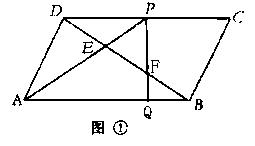
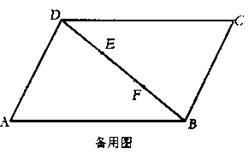
E、F为![]() ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①
ABCD的对角线DB上三等分点,连AE并延长交DC于P,连PF并延长交AB于Q,如图①
(1) 在备用图中,画出满足上述条件的图形,记为图②,试用刻度尺在图①、②中量得AQ、BQ的长度,估计AQ、BQ间的关系,并填入下表
长度单位:cm
| AQ长度 | BQ长度 | AQ、BQ间的关系 | |
| 图①中 | |||
| 图②中 |
由上表可猜测AQ、BQ间的关系是__________________
(2) 上述(1)中的猜测AQ、BQ间的关系成立吗?为什么?
(3) 若将![]() ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ、BQ间的关系是否成立?(不必说明理由)
ABCD改为梯形(AB∥CD)其他条件不变,此时(1)中猜测AQ、BQ间的关系是否成立?(不必说明理由)
25.(以下两小题选做一题,第(1)小题满分14分,第(2)小题满分为10分。若两小题都做,以第(1)小题计分)
选做第________小题.
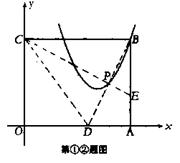
(1) 一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4。
① 如图,将纸片沿CE对折,点B落在x轴上的点D处,求点D的坐标;
② 在①中,设BD与CE的交点为P,若点P,B在抛物线![]() 上,求b,c的值;
上,求b,c的值;
③ 若将纸片沿直线l对折,点B落在坐标轴上的点F处,l与BF的交点为Q,若点Q在②的抛物线上,求l 的解析式。
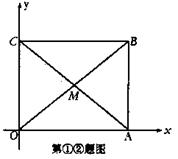
(2) 一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4。
①求直线AC的解析式;
②若M为AC与BO的交点,点M在抛物线![]() 上,求k的值;
上,求k的值;
③将纸片沿CE对折,点B落在x轴上的点D处,试判断点D是否在②的抛物线上,并说明理由。
![]() (2005宁波)27.已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB 为直径的⊙E交y轴于点D、F(如图),且DF=4,G 是劣弧A D上的动点(不与点A、D重合),直线CG交x轴于点P.
(2005宁波)27.已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB 为直径的⊙E交y轴于点D、F(如图),且DF=4,G 是劣弧A D上的动点(不与点A、D重合),直线CG交x轴于点P.
(1) 求抛物线的解析式;
(2) 当直线 CG是⊙E的切线时,求tan∠PCO的值.
(3)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.
(2005丽水)25、(本题14分)
为宣传秀山丽水,在“丽水文化摄影节”前夕,丽水电
视台摄制组乘船往返于丽水(A)、青田(B)两码头,在
A、B间设立拍摄中心C,拍摄瓯江沿岸的景色.往返过程中,船在C、B处均不停留,离开码头A、B的距离s(千米)与航行的时间t(小时)之间的函数关系如图所示.根据图象提供的信息,解答下列问题:
(1)船只从码头A→B,航行的时间为 小时、航行的速度为 千米/时;船只从码头B→A,航行的时间为 小时、航行的速度为 千米/时;
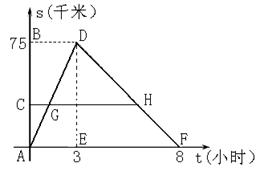 (2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=
(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=![]() ,GH=y,求出y与
,GH=y,求出y与![]() 之间的函数关系式;
之间的函数关系式;
(3)若拍摄中心C设在离A码头25千米处, ![]() 摄制组在拍摄中心C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
摄制组在拍摄中心C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
①求船只往返C、B两处所用的时间;
②两组在途中相遇,求相遇时船只离拍摄中心C
有多远.
,
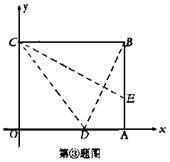
24. 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.记CD的长为t.
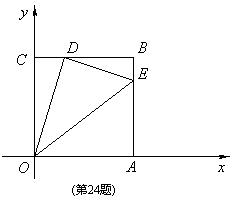 (1) 当t=
(1) 当t=![]() 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;
(2) 如果记梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由;
(3) 当OD2+DE 2的算术平方根取最小值时,
求点E的坐标.
(2005湖州)24.(本小题12分)如图,已知直角坐标系内的梯形AOBC(O为原点),AC∥OB,OC⊥BC,AC,OB的长是关于x的方程x2-(k+2)x+5=0的两个根,且S△AOC:S△BOC=1:5。
(1)填空:0C=________,k=________;
(2)求经过O,C,B三点的抛物线的另一个交点为D,动点P,Q分别从O,D同时出发,都以每秒1个单位的速度运动,其中点P沿OB由O→B运动,点Q沿DC由D→C运动,过点Q作QM⊥CD交BC于点M,连结PM,设动点运动时间为t秒,请你探索:当t为何值时,△PMB是直角三角形。
四、自选题(本题有2个小题,共10分)
注意:本题为自选题,供考生选做。自选题得分将计入本学科的总分,但考生所得总分最多为120分。
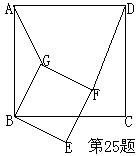 25.(本小题4分)如图,四边形ABCD和BEFG均为正方形,则
25.(本小题4分)如图,四边形ABCD和BEFG均为正方形,则![]() =________。(结果不取近似值)
=________。(结果不取近似值)
26.(本小题6分)某高速公路收费站,有m(m>0)辆汽车排队等候收费通过。假设通过收费站的车流量(每分钟通过的汽车数量)保持不变,每个收费窗口的收费检票的速度也是不变的。若开放一个收费窗口,则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过;若同时开放两个收费窗口,则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过。若要求在3分钟内将排队等候收费的汽车全部通过,并使后来到站的汽车也随到随时收费通过,请问至少要同时开放几个收费窗口?
答案:
(杭州)25. (1)常数![]() 的值为
的值为![]() (2)正方形MNPQ的边长为
(2)正方形MNPQ的边长为![]()
26. (1)2秒或12秒钟后,ΔPBQ的面积是ΔABC的面积的一半 (2)PQ=![]() 或
或![]()
(丽水)25.(本题14分)
解:(1)3、25;5、15;……………………………………………………4分
(2)解法一:设CH交DE于M,由题意:
ME=AC=x ,DM=75–x, … ……………………………………1分
∵GH//AF,△DGH∽△DAF , …………………………………1分
∴ ![]() ,即
,即![]() , ………………………………2分
, ………………………………2分
∴ y=8![]() . …………………………………………………1分
. …………………………………………………1分
解法二:由(1)知:A→B(顺流)速度为25千米/时,B→A(逆流)速度为15千米/时,y即为船往返C、B的时间.
y=![]() ,即y=8
,即y=8![]() .(此解法也相应给5分)
.(此解法也相应给5分)
(3)①当x=25时,y=8![]() (小时).……………………2分
(小时).……………………2分
②解法一:
|
|
|
|
|
a–b=15 b=5
船到B码头的时间t 1=![]() =2小时,此时橡皮艇漂流了10千米.
=2小时,此时橡皮艇漂流了10千米.
设船又过t2小时与漂流而下橡皮艇相遇,
则(5+15)t2=75–25–10,∴t2=2. ……………………………1分
∴船只离拍摄中心C距离S=(t 1+ t2)×5=20千米. …………1分
解法二:
设橡皮艇从拍摄中心C漂流至P处与船返回时相遇,
得![]() ,∴CP=20千米.
,∴CP=20千米.
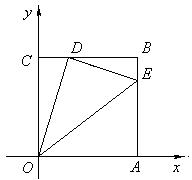 (2005浙江学业考试)24. 解:(1)易知△CDO∽△BED,
(2005浙江学业考试)24. 解:(1)易知△CDO∽△BED,
所以![]() ,即
,即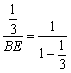 ,得BE=
,得BE=![]() ,则点E
,则点E
的坐标为E(1,![]() ).……………………………(2分)
).……………………………(2分)
设直线DE的一次函数表达式为y=kx+b,直线经过两点D(![]() ,1)和E(1,
,1)和E(1,![]() ),代入y=kx+b得
),代入y=kx+b得![]() ,
,![]() ,故所求直线DE的函数表达式为y=
,故所求直线DE的函数表达式为y=![]() .…………………………(2分)
.…………………………(2分)
(注:用其它三角形相似的方法求函数表达式,参照上述解法给分)
(2) 存在S的最大值.……………………………………………………………………1分
求最大值:易知△COD∽△BDE,所以![]() ,即
,即![]() ,BE=t-t2,……1分
,BE=t-t2,……1分
![]() ×1×(1+t-t2)
×1×(1+t-t2)![]() .………………………………………………1分
.………………………………………………1分
故当t=![]() 时,S有最大值
时,S有最大值![]() .………………………………………………………2分
.………………………………………………………2分
(3) 在Rt△OED中,OD2+DE 2=OE2,OD2+DE 2的算术平方根取最小值,也就是斜边OE取最小值.……………………………………………………………………………1分
当斜边OE取最小值且一直角边OA为定值时,另一直角边AE达到最小值,……1分
于是△OEA的面积达到最小值,………………………………………………………1分
此时,梯形COEB的面积达到最大值.………………………………………………1分
由(2)知,当t=![]() 时,梯形COEB的面积达到最大值,故所求点E的坐标是
时,梯形COEB的面积达到最大值,故所求点E的坐标是
(1,![]() ).…………………………………………………………………………………1分
).…………………………………………………………………………………1分
注:(3)小题的另一种解法:![]() =
=![]() ,猜想当t=
,猜想当t=![]() 时,
时,![]() 取最小值(其值
取最小值(其值![]() ).…………………………………1分
).…………………………………1分
运用计算器可以验证猜想是正确的,………………………………………………3分
此时点E的坐标是(1,![]() ).…………………………………………………………1分
).…………………………………………………………1分
