2006年初中毕业考试数学模拟试卷

注意事项：

　　　 1、试卷满分120分，答卷时间120分钟；

　　　 2、允许使用科学计算器。

题号	一	二	三	总分	复核
得分

得 分	评卷人	一、选择题（下列各题中的四个选项只有一个正确，请将正确选项的字母标号填在题后的括号内，每小题3分，共24分）

1、世界文化遗产长城总长约6 700 00 m，用科学记数法可表示为　　　　　　　　　　　　　　　　　（　）

　 A、6.7×10⁵m　　 B、6.7×10^-5m　　　　　　C、6.7×10⁶m　　　　D、6.7×10^-6m　　

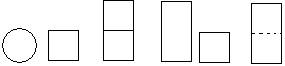
2、小明从正面观察下图所示的两个物体，看到的是　　　　　　　　　　　　　 （　）

　　　　正面　　　　　　　　　　　　A　　　　　 B　　　　　 C　　　　　 D

3、在同一时刻，身高1.6米的小强影长1.2米，旗杆影长15米，则旗杆高为　　（　）

　 A、16m　　　 B、18m　　　　　C、20m　　　　　D、22m

4、不等式组的解集在数轴上可表示为　　　　　　　　　　　　　　 （　）

　 A、　　　　　　　　 B、

　 C、　　　　　　　　 D、

5、下列事件：

　 A、掷一枚六个面分别标有1~6的数字的均匀骰子，骰子停止转动后偶数点朝上

　 B、从一副扑克牌中任意抽出一张牌，花色是红桃

　 C、任意选择电视的某一频道，正在播放动画片

　 D、在同一年出生的367名学生中，至少有两人的生日是同一天。

　 确定事件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　）

6、为了了解本校九年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25~30次的频率是　　　　　　　　　　　　　 （　）

　 A、0.1　　　 B、0.2　　　

　 C、0.3　　　　 D、0.4

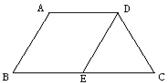
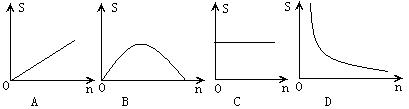
7、如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是　　　　　　　　（　）

　 A、3　　　　　　　　 B、12　　　

　 C、15　　　　　　　　　　D、19

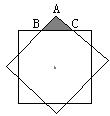8、如图，两块完全重合的正方形纸片，如果上面的一块绕正方形的中心O左0°~90°的旋转，那么旋转时露出的△ABC的面积（S）随着旋转角度（n）的变化而变化，下面表示S与n关系的图象大致是　　　　　　　　　　　　　　　　 　　　　 （　）

　

得 分	评卷人	二、填空题（每小题3分，共18分）

9、计算x²·x³=　　　　　　  .

10、代数式4a可表示的实际意义是　　　　　　　　　　　　　　　　　　　　　　

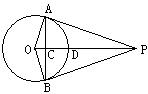11、如图，P是⊙O外一点，OP垂直于弦AB于点C，交于点D，连结OA、OB、AP、BP。根据以上条件，写出三个正确结论（OA=OB除外）

①　　　　　　 ；②　　　　　　 ；③　　　　　　 。

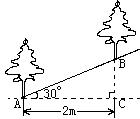
12、如图，沿倾斜角为30°的山坡植树，要求相邻俩棵树的水平距离AC为2cm，那么相邻两棵树的斜坡距离AB约为 　　　m。（精确到0.1m，可能用到的数据，）。

13.从全市5000份试卷中随机抽取400份试卷，其中有360份成绩合格，估计全市成绩合格的人数约为　　　　　  人。

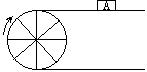14、如图，当半径为30cm的转动轮转过120°角时，传送带上的物体A平移的距离为　　 cm。

得 分	评卷人	三、解答题（共78分）

15、（5分）解方程：x²+2x-3=0。

16、（5分）化简求值：，其中x=2。

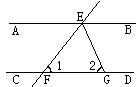17、（6分）如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF交CD于点G，∠1=50°，求∠2的度数。

18、（6分）在一条东西走向的马路上，有青少年宫、学校、商场、医院四家公共场所。已知请少年宫在学校东300米，商场在学校西200米，医院在学校东500米。若将马路近似的看成一条直线，以学校为原点，向东方向为正方向，用1个单位长度表示100米，

　 （1）在数轴上表示出四家公共场所的位置；

　 （2）列式计算青少年宫与商场之间的距离。

19、（6分）如图，平行四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F。

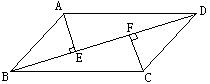　 （1）写出图中每一对你认为全等的三角形；

　 （2）选择（1）中的任意一对进行证明。

20、（6分）一布袋中有红、黄、白三种颜色的球各一个，它们除颜色外其它都一样。小亮从布袋中摸出一个球后放回去摇匀，再摸出一个球。请你利用列举法（列表或画树状图）分析并求出小亮两次都能摸到白球的概率。

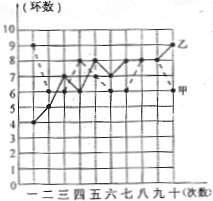21、（8分）射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示：

　 （1）根据右图所提供的信息填写下表：

	平均数	众数	方差
甲	7		1.2
乙			2.2

　 （2）如果你是教练，会选择哪位运动员参加比赛？请说明理由。

22、（8分）在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表：

蟋蟀叫次数	…	84	98	119	…
温度（℃）	…	15	17	20	…

　 （1）根据表中数据确定该一次函数的关系式；

　 （2）如果蟋蟀1分钟叫了63次，那么该地当时的温度大约为多少摄氏度？

23、从下面两题中任选一题进行解答（（1）题6分，（2）题8分）

　 （1）先在左面的一块方格纸上画一个轴对称图形作为基础图形，再将基础图形去掉或添上一部分，使新图形仍为轴对称图形，画在右面的方格纸上。

　 （2）先在左面的一块方格纸上画一个轴对称图形作为基础图形，再将基础图形的一部分平移或旋转到剩余图形的某一位置组成新的图形，使新图形仍为轴对称图形，画在右面的方格纸上。

24、（10分）在湖的两岸A、B间建一座观赏桥，由于条件限制，无法直接度量A、B两点间的距离。请你用学过的数学知识按以下要求设计一测量方案。

　 （1）画出测量图案；

　 （2）写出测量步骤（测量数据用字母表示）；

　 （3）计算AB的距离（写出求解或推理过程，

结果用字母表示）。

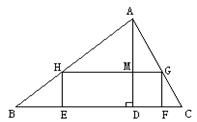
25、（10分）如图，要在底边BC=160cm，高AD=120cm，的△ABC铁皮余料上截取一个矩形EFGH，使点H在AB上，点G在AC上，点E、F在BC上，AD交HG于点M，此时。

　 （1）设矩形EFGH的长HG=y，宽HE=x，确定y与x的函数关系式；

　 （2）当x为何值时，矩形EFGH的面积S最大；

　 （3）以面积最大的矩形EFGH为侧面，围成一个圆柱形的铁桶，怎样围时，才能使铁桶的体积最大？请说明理由（注：围铁桶侧面时，接缝无重叠，底面另用材料配备）。