湖北省黄冈市2006年初三年级调研考试

　　　　  数　学　试　题　　 (课改实验区)

(满分：120分　　  考试时间：120分钟)

 

题号	1-6	7--11	12	13	14	16-17	18	19	20	21	22	总分
得分

一、填空题（每空题3分，共24分）

1.　　　　 计算：=　　　 ；4的平方根是　　  ；在天气预报中，零上5摄氏度用表示，那么零下5摄氏度表示为　　　　　　  。

2.　　　　 因式分解：=　　　　　　　  。

3.　　　　 若，则代数式可化简为　　　　　  。

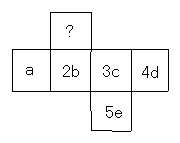
4.　　　　 如图，是一个正方体纸盒的平面展开图，当攒成正方体后，“？”所表示的单项式与它对面的正方形内的式子的和为0，则“？”所表示的单项式是　　　　　　 。

5.　　　 汽车刹车距离与速度之间的函数关系是，在一辆车速为的汽车前方处，发现停放一辆故障车，此时刹车　　　　　 有危险（填：“会”或“不会”）

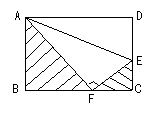
6.　　　 如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F点处，已知，则︰=　　　　　　　  。

二、单项选择题（请将下列各题中唯一正确的答案序号填入题后的括号内，不填、错填或多填均不得分，每小题3分，共15分）

7、下列运算中正确的是（　　　　 ）

　 A、　　　　　　　　 B、

C、　　　　　  D、

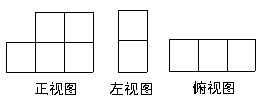8、如图，是由一些相同的小正方体搭成的几何体的三视图，那么搭成这个几何体的小正方体的个数为（　　  ）

　 A、5个　　　　　　  B、6个　　

C、7个　　　　　　  D、8个

9、已知反比例函数的图象上两点A（，），B（，），当时，有，那么的取值范围是（　　  ）www.1230.org

　 A、　　　　B、　　　　  C、　　　　 D、

10、如图，是某公司年3年的当年资金投放总额与当年利润统计示意图，根据图中的信息判断：①2004年的利润率比2003年的利润率高2%；②2005年的利润率比2004年的利润率 高8%；③这三年的利润率为14%；④这三年中2005年的利润率最高。其中的正确的结论共有（　　　）

　A、1个　　　　B、2个　　　　C、3个　　　　　D、4个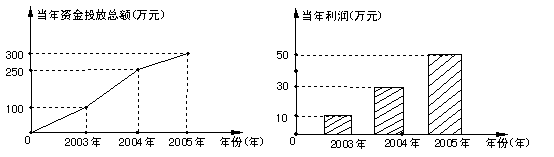

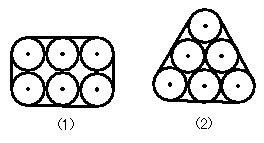11、图（1），图（2）是用两种方法把6根圆形钢管用钢丝捆扎的截面图。设图（1）、图（2）两种方法所需钢丝绳的长度分别为、（不记接头部分），则、的大小关系为（　　）

A、　　 　B、

C、　　 　D、不能确定

三、解答下列各题（共3道题，共21分）

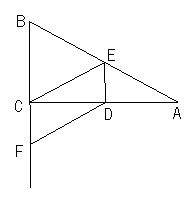
12、（本题满7分）已知：如图，△ABC中，，点D、E分别是AC、AB的中点，点F在BC的延长线上，且∠CDF＝∠A。求证：四边形DECF是平行四边形。

13、（本题满7分）某服装店的老板在武汉看到一种夏季衬衫，就用8000元购进若干件，以每件58元的价格出售，很快售完，又用17600元购进同种裤衩，数量是第一次的2倍，每件进价比第一次多了4元，服装店仍按每件58元出售，全部售完，问该服装店这笔生意盈利多少元？ www.1230.org 初中数学资源网 录入

14、（本题满7分）小兵和小欣两同学同时抛掷三枚硬币。在抛掷前，小兵说：“硬币落地后，若全是正面或全是反面，则是输；若硬币为两正一反或两反一正，则我赢。”

（1）若你是小欣，你同意小兵制定的游戏规则吗？请通过计算小兵制定的游戏的概率（利用树状图或列表法）来说明理由。

（2）若你是小欣，请重新充计一个公平的游戏规则。

四、多项选择题（本题满12分，在每个小题所给的四个选项中，至少的一项是符合题目要求的，请把所有符合题目要求的答案予号填入题后的括号内，全对得4分，对而不全的酌情扣分；有对有错、全错或不答均得零分）

15、下列说法错误的是（　　　　）

A、某资深彩民买了一张2元的体育彩票中了一等奖，他又买了1000元，则他100%会再中奖。

B、为调查一个省的年人收入情况，可调查全省各城市职工的年人均收入。

C、某牙膏广告语描述的“牙好，胃口就好，身体倍棒，吃嘛嘛香。”的事件是必然事件。

D、一只不透明的袋内装有2个红球、3个白球（这些球除颜色外没有其它区别），从中任意取出一球，则取得红球的概率是。

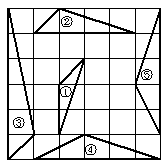
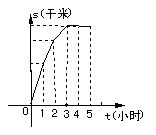16、如图，在正方形网格上有5个三角形①、②、③、④、⑤，其中与①（不抱括①）相似的三角形有（　　　　）

A、②　　　　B、③　　　　C、④　　　　D、⑤

17、某人骑呈外出，所行的路程（千米）与时间（小时）的函数关系如图所示，现有下列四种说法，正确的是（　　）

A、第2小时到第3小时的速度比第1小时到第2小时的速度快。

B、第2小时到第3小时的速度比第1小时到第2小时的速度慢。

C、第3小时后已停止前进。

D、第3小时后保持匀速前进。

五、解答下列问题（共5道题，共48分）

18、（本题满6分）某班要从小王和小李两名同学中挑选一人参加学校数学竞赛，在最近的五次选拔测试中，他俩的数学成绩分别如下：

次数 姓　成绩 名　 （分）	1	2	3	4	5
小王	60	75	100	90	75
小李	70	90	80	80	80

根据上表解答下列列问题：

（1）完成下表：

姓名	极差（分）	平均成绩（分）	中位数（分）	众数（分）	方差
小王	40	80	75	75	190
小李					40

（2）在这五次测试中，成绩比较稳定的同学是谁？苛将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？

（3）历届比赛表明，成绩达到80分（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为应选谁参加比赛比较合适？说明你的理由。

19、（本题满8分）如图，AB、AC分别是⊙O的直径和弦，D为劣弧上一点，DE⊥AB于点H，交⊙O于点E，交AC于占F，P为ED的延长线上一点。

（1）点D在劣弧的什么位置时，才能使，为什么？

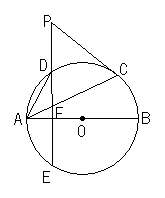（2）当PC=PF时，求证：PC与⊙O相切。

20、（本题满分8分）随着科学技术的发展，机器人早已能按照设计的指令完成各种动作。在坐标平面上，根据指令机器人能完成下列动作：先原地顺时针旋转角度，再朝其面对的方向沿直线行走距离。

（1）填空：如图，若机器人在直角坐标系的原点，且面对轴的正方向，现要使其移动到点A（2，2），则给机器人发出的指令应是　　　　　　　　　　 ，

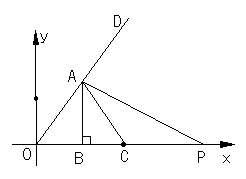（2）机器人在完成上述指令后，发现在P（6，0）处有一小球正向坐标原点做匀速直线运动，已知小球的滚动速度与机器人行走的速度相同，若忽略机器人原地旋转的时间。请你给机器人发一个指令，使它能最快截住小球。（如图，点C为机器人最快截住小球的位置。）（角度精确到度；参考数据：

21、（本题满分10分）

某公司生产一种产品，每件成本3元，售价4元，年销售量20万件，为获得更好的效益，公司准备拿出一定资金做广告，根据经验，设广告费万元，做广告后的年销售量是原销售量的倍，且与的关系如图所示。图中AB是线段，BCD是抛物线段，DE是射线，如果把利润看成是销售总额减去成本费和广告费，（1）写出与的函数关系式；（2）试比较广告费分别为万元和万元时，产品销售量的大小；（3）试写出年利润（万元）与广告费（万元）之间的函数关系式。

22、（本题满分16分）如图，直角坐标系内的梯形AOBC（O为原点），AC∥OB，AO⊥OB，AC=1，OA=2，BO=5。

（1）求经过O，C，B三点的抛物线的解析式；

（2）延长AC交抛物线于点D，求线段CD的长；

（3）在第（2）小题的条件下，动点P、Q分别从O、D同时出发，都以每秒1个单位的速度运动，其中点P沿OB由O→B运动，点Q沿DC由D→C运动，过点Q作QM⊥CD交BC于点M，连结PM，设动点运动时间为秒，请你探索：当为何值时，△PMB是直角三角形。

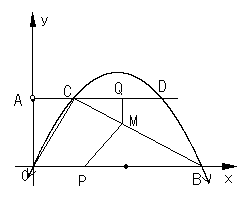
参考答案

1、；，－5℃　　 2、　　 3、　 4、　　5、会　　6、4：1 7、D　　 8、A　　9、C　　  10、B　　　11、A

12、证明：∵D，E分别是AC，AB的中点，

∴DE∥BF

∴

∵

∴

∴∠ADE=∠DCF，又∠CDF=∠A，CD=DA

∴△CDF≌△DAE。………………………………………………………（3分）

∴DE=CF。

∵DE∥CF，

∴四边形DECF是平行四边形。………………………………………（7分）

13、解法不唯一，现提供其中一种解法。

解：设第一次购进衬衫件，依题意得，

　…………………………………………………………（3分）

解得，　　…………………………………………………………（4分）

经检验，是原分式式方程的解。………………………………………（5分）

∴。

∴该服装店这笔生意可盈利9200元。…………………………………………（7分）

14、解：（1）不同意小兵制定的游戏规则。………………………………………（1分）

　　　　同时抛掷三枚硬币一次，各种事件出现的机会如下图：（4分）

　　　　

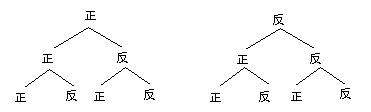
则全是正面的有1次，全是反而的有1 次，两正一反的有3次，两反一正的有3次，所以P（全是正面或反面）=，P（两正一反或两反一正）=。所以小兵制定的游戏规则不公平。…………………………………………………………………………（6分）

（2）答案不唯一，如：同时抛掷三枚硬币一次，出现两反一正的一方赢，出现两正一反的则另一方赢。

15、ABC　　 16、CD　　　　  17、BC

18、解：（1）从左至右依次填：20，80，80，80；………………………………（2分）

　 （2）在这五次考试中，成绩比较稳定的是小李，………………………………（3分）

　　　　　  小王的优秀率为40%，小李的优秀率为80%。……………………………（4分）

　 （3）只需设计一种方案即可。

　　方案一：我选小李去参加比赛，因为小李的优秀率高，有4次得80分，成绩比较稳定，获奖机会大。

方案二：我选小王去参加比赛，因为小王的成绩获得一等奖的机率较高，有2次80分以上（含90分）因些有可能获得一等奖。

（注：答案不唯一，考生可任选其中一人，只要分析合理，都可给分，若选两人都去参加，不合题意）。…………………………………………………………………………（6分）

19、（1）解：当点D是的中点时，，连结AE

　　 ∵，∴∠DAF=∠DEA。∵∠ADF=∠EDA，∴△ADF∽△DEA。

∴∠，…………………………………………（4分）

（2）连结CO，则∠OCA=∠FAH。∵PC=PF，∴∠PCF=∠PFC=∠AFH。

∵DE⊥AB于H，∴∠OCA+∠PCF=∠FAH+∠AFH=90⁰，即OC⊥PC。

∴PC与⊙O相切。…………………………………………………………… （8分）

20、（1）[，]。……………………………………………………………（3分）

　 （2）解：由题意可知，PC=AC，设，则。在Rt△ABC中，，解得。…………………………………………（6分）

　 又，，∴∠CAB=，

∴…………………………………………………（8分）

∴指令为[，]…………………………………………………………………… （8分）

21、（1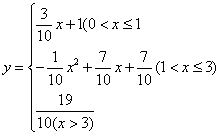） ，………………………………………（3分）

　 （2）当时，（倍），当时，

　　 ∵，∴当广告费为万元时，产品销售量较大；………………………（7分）

　 （3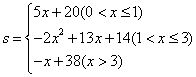），…………………………………………（10分）

22、解：（1）由题意可知，O（0，0），C（1，2），B（5，0）。……………………（2分）

　 设经过O，C，B三点的抛物线的解析式为。

　 则可得，，∴。…………………………（4分）

　（2）当时，则，解得，∴CD=4-1=3。……（7分）

　（3）延长QM交轴轴于点N，

　 ①若MP⊥OB，则四边形AOPQ是矩形。

∴AQ=OP，∴，∴……………………………………………………（11分）

②PM⊥BM，则△PNM∽△MNB。∴

∵CQ∥NB，∴△CQM∽△BNM，则有。

∴www.1230.org 初中数学资源网 录入

∵。解得（舍去），。……………………（15分）

∴综上所述，或时，△PMB是直角三角形。………………………（16分）