2006年九年级数学中考第二次模拟考试卷
本试卷共130分，考试时间120分钟 2006-5-18
成绩_______
一、填空题（每空2分，共32分）
1、
的相反数为________;
的算术平方根是_________,计算
的结果是_____
2.. 分解因式：
_______________.
3. 函数y=中，自变量x的取值范围是__________.
4. 某种禽流感病毒变异后的直径为
米，将这个数写成科学记数法是____________________.
5. 反比例函数
的图象经过点
，则
的值为_________.
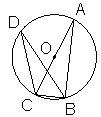
6. 如图，点D在以AC为直径的⊙O上，
如果∠BDC=20°，那么∠ACB的度数
为__________.
7. 二次函数
的图象的对
称轴是____________.
8. 某圆锥的正视图是一个边长为
的等边三角形，那么这个圆
锥的侧面积是______________.
9.在比例尺为1∶40000的地图上，某经济开发区的面积为20cm2，那么，该经济开发区的实际面积为
km2．
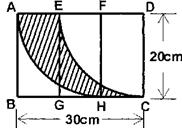
10.如图，四边形ABCD是一个矩形，E、F、G、H分别是边AD、BC上的三等分点，请你根据图中的数据求阴影部分的面积为 cm2.
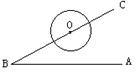11. 如图,已知∠ABC=30°,以O为圆心、2cm为半径作⊙O, 使圆心O在BC边上移动, 则当OB= cm时, ⊙O与AB相切.
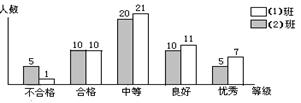12. 右图反映了某校初二(1)、(2)两班各50名学生电脑操作水平等级测试的成绩,其中不合格、合格、中等、良好、优秀五个等级依次转化为50分、60分、70分、80分、90分,试结合图形计算: ①(1)班学生成绩众数是 分;
②(2)班学生成绩的方差是 .
13. 某项科学研究需要以30分钟为一个时间单位, 并记研究那天上午10时为0，10时以前记为负，10时以后记为正. 例如那天9:30记为－1，10:30记为1等等, 依此类推,那天上午7:30应记为_____.
二、选择题（每小题3分，共21分）
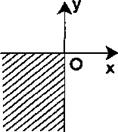
14.在一次科学探测活动中，探测人员发现一目标在如图所示的阴影区域内，则该目标的坐标可能是------------（ ）
A. 
B. 
C. 
D. 
15.面积为10的正方形的边长
满足下面不等式中的--------------（ ）
A.1＜＜3 B. 3＜＜4 C. 5＜＜10 D. 10＜＜100
16. 如图表示了某个不等式的解集, 该解集所含的整数解的个数是--( )
A. 4 B. 5
C. 6 D.7
17. 两条不平行的直线被第三条直线所截,下列说法可能成立的是------( )
A.同位角相等 B.内错角相等 C.同旁内角相等 D.同旁内角互补
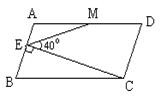18. 如图，在□ABCD中，AD=2AB，M是AD的中点，CE⊥AB于点E，∠CEM=40°，则∠DME是（ ）
A. 150° B. 140° C. 135° D. 130°
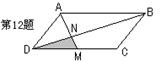19．如图，在□ABCD中，如果点M为CD中点，AM与BD相交于点N，那么S△DMN∶S□ABCD为（ ）
A. 1∶12 B. 1∶9 C. 1∶8 D. 1∶6
20．计算机利用的是二进制数，它共有两个数码0、1，将一个十进制数转化为二进制数，只需要把该数写成若干个2n数的和，依次写出1或0即可. 如十进制数19=16＋2＋1=1×24＋0×23＋0×22＋1×21＋1×20, 转化为二进制数就是10011, 所以19是二进制下的5位数. 问：2005是二进制下的几位数( )
A. 10 B. 11 C. 12 D. 13
三、解答题（21、22题每小题5分，23题8分，24题6分，共24分）
21. 
22.
解方程组：
23. 自然数1到n的连乘积，用n！表示，这是我们还没有学过的新运算（高中称为阶乘），这种运算规定：1！=1 ，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，…在这种规定下，请你解决下列问题：
（1） 计算 5！=
（2） 已知x为自然数 ，求出满足下列等式的x：
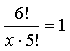
（3） 分解因式
24.已知如图，在□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F.
(1)求证：CD=FA.
(2)若使∠F=∠BCF，□ABCD的边长之间还需再
添加什么条件？请你补上这个条件，并进行证明
（不要再添加辅助线）
四、解答题：（25、26题每小题8分，27、28题每小题9分，共34分）
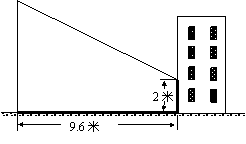25.赵亮同学想利用影长测量学校旗杆的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6米和2米，请你计算出学校旗杆的高度.
26.某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
| 年 度 | 2002 | 2003 | 2004 | 2005 |
| 投入技改资金z(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本，(万元／件) | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据，找出一个适合上表的y与x之间的关系式，
(2)按照这种变化规律，若2006年已投人技改资金5万元．
①预计生产成本每件比2005年降低多少万元?
②如果打算在2006年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元（结果精确到0.01万元)?
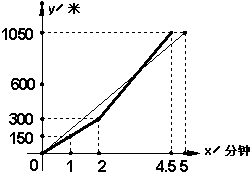
27．端午节期间，南京市都将举行龙舟比赛。甲、乙两支龙舟队在比赛时的路程y（米）与时间x（分钟）之间的函数图象如图所示（其中实线表示乙队，虚线表示甲队）.请你根据图象回答下列问题：
（1）1.8分钟时，哪支龙舟队处于领先位置？
（2）在这次龙舟赛中，哪支龙舟队先到达终点？先到达多少时间？
（3）求乙队加速后，路程y（米）与时间x（分钟）之间的函数关系式。
| |
28. 在平面直角坐标系中有一点P0（1，0），O为坐标原点.将线段OPO绕点O按逆时针旋转45º得线段OP1，延长OP1到点P2，使OP2= 2OP1.再将OP2绕点O按逆时针方向旋转45º得线段OP3 ，延长OP3到点P4，使OP4= 2OP3.照此规律，继续下去.试写出P2、P7、P100三个点的坐标.
 |
四、动脑筋想一想：（29题9分，30题10分，共19分）
29．旋转是一种常见的全等变换，图（1）中△ABC绕点O旋转后得到
，我们称点A和点
、点B和点
、点C和点
分别是对应点，把点O称为旋转中心。
（1）观察图（1），想一想，旋转变换具有那些特点呢？请写出其中三个特点：________________________________________________________________
___________________________________________________________________
___________________________________________________________________
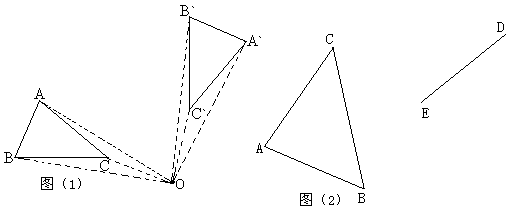（2）图（2）中，△ABC随时针旋转后，线段AB的对应线段DE，请你利用圆规、直尺等工具，①作出旋转中心，②作出△ABC绕点O旋转后的△DEF。（要求保留作图痕迹。）
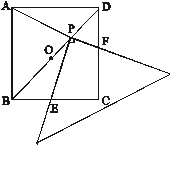
30. 如图，
是边长为
的正方形
的对称中心，
为
上一点，
（
），连结
，把一个边长均大于
的直角三角板的直角顶点放置于点处，让三角板绕点旋转，旋转时保持三角板的两直角边分别与正方形的
、
边（含端点）相交，其交点为
、
.
（1）在旋转过程中，
的长能否与的长相等？若能，请作出此时点的位置，并给出证明，若不能，请说明理由.
（2）探究在旋转过程中，线段
与长的大小关系，并对你得出的结论给予证明.
（3）探究在旋转过程中,四边形
的面积
是否发生变化？若不变化，求出定值；若发生变化，试求出面积的变化范围（用含、
的代数式表示）.
 |
答案：
一、1、2；4；a
2、x（x+2）（x-2）
3、x≥-2
4、1.2×10-7
5、-2
6、70°
7、x=1
8、9/2 π
9、3.2
10、200
11、4
12、70；120
13、-5
二、D、B、B、C、A、A、B
三、21、2x2
22、x=6
23、(1)120
(2)x=6
(3)(x-100)(x+99)
24、(1)略
(2)条件：BC=2CD
四、25、10
26、（1）y=18/x
（2）0.4；0.63
27、（1）甲队
（2）乙队先到达0.5分钟
（3）y=300x-300
28、P2：（,）
P7：（-8，0）
P100：（0，250）
五、29、略
30、（1）当运动到
位置时（点
与
重合）时（以为圆心，以
为半径画弧得与
的另一个交点
），=. 证明略
（2）探究结论:在旋转过程中，线段
.证明略
（3）探究结论:在旋转过程中,四边形的面积发生变化.
面积的取值范围是: 
.