2006年初三数学中考模拟测试题 _（C.）

一、选择题(把下列各题中唯一正确答案的序号填在题后的括号内，每小题3分，共24分)

1、下列式子结果是负数的是（　　）

　　A. －　　  　 B. －(－3)　　　　C. 　　　　 D.

2、小亮在镜中看到身后墙上的时钟如下, 你认为实际时间最接近8:00的是 (　　)

　　 　　 　　 

A. 　　　　　　　　　B. 　　　　　 　 C. 　　　　　　　D.

3．矩形的两邻边长分别为3和6，若以较长一边为直径作圆，则与圆相切的矩形的边共有

　　A. 4条 　　　 　　B. 3条　 　　 　　C. 2条　 　　 　　D. 1条

4．两个顶角相等的等腰三角形框架，其中一个三角形框架的腰长为6，底边长为4，另一个三角形的

框架的底边长为2，则这个三角形框架的腰长为

　　A. 6　　　　　　　B. 5 　　　　　　 C. 4 　　　　　　 D. 3

5. 在高速公路上，一辆2米长、时速110公里的汽車打算超越一辆6米长、时速100公里同向行驶的卡車.

则汽車从开始追及到超越卡车，总共费时（　　　　）秒.

A　　2.54 　 B　 2.88　　C　 4.12　  D　 5.64　

6．一张桌子上摆放着若干个碟子，从三个方向看，三种视图如下图所示,，则这张桌子上共有碟子为

　　A. 6个　　　　　　B. 8个　　　　　　C. 12个　　　　　 　D. 17个

7.某出版社计划出版一套百科全书，固定成本为10万元，每印制一套需增加成本20元．如果该书以每套100元出售，卖出后需付书款的30%给承销商．若出版社要盈利10%，那么该书至少应发行（精确到千位）

A. 2千套　　　　　B. 3千套　　　　 C. 4千套　　　　　D. 5千套

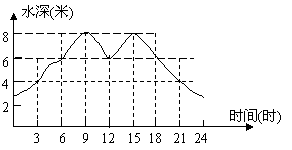8．一港口受潮汐影响，某天24小时内港内水深变化大致如下图．港口规定：为了保证航行安全，只有当船底与水底间的距离不少于4米时，才能进出该港．一艘吃水深度（即船底与水面的距离）为2米的轮船进出该港的时间最多为（单位：时）

　　A. 3 　　　　　　 B. 6

　　C. 12 　　　　　　D. 18

二、填空题：(每小题3分，共24分)

9．在实数—2，π，，中，无理数有_____个　

10．纳米是0.米，流感病毒的直径是90纳米，用科学记数法表示是______米．

11．点(α，β)在反比例函数的图象上，其中α、β是方程的两根，则．

12.若整个正方形的面积是12,那么你认为红色部分图案

的面积是　　　　　　　　　  ．

　　　　　　　　　　　　　　　　 第13题

13．如图，圆内接△ABC中，D是BC边的中点，E是AB边的中点，F是AC边的中点，连结DE、DF，要使四边形AEDF为菱形，应补充的一个条件是　　　　　　　  ．（只要填上一个你认为恰当的条件即可）

14．在日常生活中，你会注意到有一些含有特殊数学规律的车牌号码，如：吉A80808　、吉A22222、

吉A12321等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给以对称的美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8和9开头且有五个数字的“数字对称”牌照，那么最多可制作　　　　个

15. 将正偶数按下表排列成5列：

	第1列	第2列	第3列	第4列	第5列
第一行		2	4	6	8
第二行	16	14	12	10
第三行		18	20	22	24
第四行	32	30	28	26
……		…	…	…	…

根据表中的规律，偶数2006应排在第　　　　行，第　　　列；

16. 如图，矩形ABCD的长AB=4cm，宽AD=2cm．O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线的顶点是O，关于OP对称且经过C、D两点，则图中阴影部分的面积是　　　　  cm²．

三、解答题：(每小题6分，共24分)

17. 如图，△ABC为等边三角形，表示其边长的代数式均已标在图上.

求代数式（）²×的值.

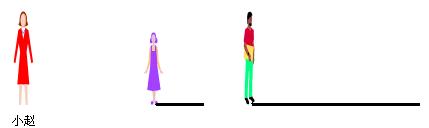
18.确定图中路灯灯泡的位置，并画出小赵在灯光下的影子；

 

19. 如图，AB与圆O相切于点C，OA=OB，圆O的直径为8，AB=10，求OA的长

　　　　　　　　　　　　　　  （第17题）　　　　　　　　  （第18题）

20. 如图是某处公路的示意图，AB=1 500米，AC=900米，AC⊥BC.如果一辆农用车以18千米/时的速度行使，那么它从A直接到B与从A经过C到B 相比较，可以节约多少时间？

四、解答题：(每小题7分，共14分)

21. 试编一道生产、生活中符合a=bc型的数量关系的应用题.要求：（1）用“行程问题”、“工程问题”、“浓度问题”、“单价、数量与总价问题”以外的实际素材编写；（2）保证应用题的科学性，数据符合实际；（3）写出完整的解答过程.

22. 有5根木棒，长度分别是2，3，4，5，6（单位：cm），现在要估计从中随机抽取三根恰好能搭成三角形的概率，如果身边没有木棒，你能设计出两种不同的模拟实验代替实际操作吗？请列举出来。并且写出其中一种的具体方案。

五、解答题：(每小题9分，共18分)

23..如图是某段河床横断面的示意图. 查阅该河段的水文资料，得到下表中的数据：

x（cm）	5	10	20	30	40	50
y（cm）	0.125	0.5	2	4.5	8	12.5

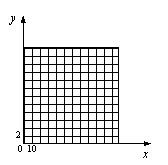
（1）请你以上表中的各对数据（x，y）作为点的坐标，

尝试在下面所给的坐标系中画出y关于x的函数图像；

（2）①填写下表：

x	5	10	20	30	40	50
x2/y

②根据所填表中数据呈现的规律，猜想出用x表示y的二次函数关系式：___________;

（3）当水面宽度为36m时，一艘吃水深度（船底部到水面的距离）为1.8m的货船能

否在这个河段安全通过？为什么？

24. 观察下列由棱长为1的小立方体摆成的图形，寻找规律：

如图1中：共有1 个小立方体，，其中1个看得见，0个看不见；如图2中：共有8个小立方体，其中7个看得见，1个看不见；如图3中：共有27个小立方体，其中有19个看得见，8个看不见；……，

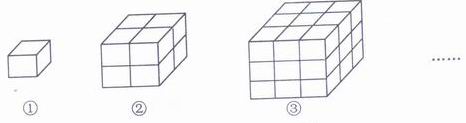
（1）　　　 请你画出②的俯视图；

（2）　　　 照此规律下去，请你判断第⑥个图中有多少个小立方块？

六、解答题：(每小题10分，共20分)

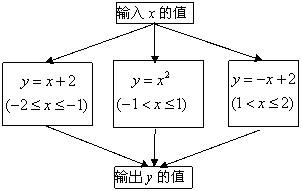
25．(02海淀区)如图所示的程序是函数型的数值转换程序，其中．

(1)若输入的x值为， 求输出的结果y,

(2)事件“输入任一符合条件的x，其输出的结果y是一个非负数”，是一个必然事件吗？说说你的理由．

(3)若所输入的x的值是满足条件的整数，求输出结果为0的概率．

26．为了测量校园内一棵不可攀的树的高度，学校数学应用实践小组做了如下的探索：

实践一：根据物理学中的反射定律，利用一面镜子和一根皮尺，设计如右示意图的测量方案：把镜子放在离树（AB）8.7米的点E处，然后沿着直线BE后退到点D，这是恰好在镜子里看到树梢顶点A，再用皮尺量得DE=2.7米，观察者目高CD=1.6米，请你计算树（AB）的高度．（精确到0.1米）

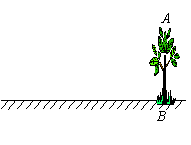
实践二：提供选用的测量工具有：①皮尺一根；②教学用三角板一副；③长为2.5米的标杆一根；④高度为1.5米的测角仪（能测量仰角、俯角的仪器）一架。请根据你所设计的测量方案，回答下列问题：

（1）在你设计的方案中，选用的测量工具是（用工　

具的序号填写）　　　　　　　　　　　 

（2）在右图中画出你的测量方案示意图；

（3）你需要测得示意图中的哪些数据，并分别用a、b、c、α等表示测得的数据：

　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　 

（4）写出求树高的算式：AB=　　　　　　　　　　　　　　　 

七、解答题：(第27题12分，第28题14分，共26分)

257已知动点P以每秒2cm的速度沿图甲的边框按从B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6，试回答下列问题：

（1）图甲中BC的长是多少？

（2）图乙中的a是多少？

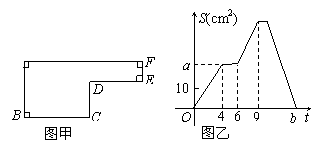（3）图甲中的图形面积是多少？

（4）图乙中的b是多少？

28.某衡器厂的RGZ-120型体重秤，最大称量120千克，你在体检时可看到如图10显示盘．已知，指针顺时针旋转角x(度)与体重y(千克)有如下关系：

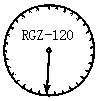
图10

　　(1)根据表格的数据在平面直角坐标系中描出相应的点，顺次连结各点后，你发现这些点在哪一种图象上？合情猜想符合这图形的函数解析式．

　　(2)验证这些点的坐标是否满足函数解析式，归纳你的结论(写出自变量x的取值范围)；

　　(3)当指针旋转到158.4度的位置时，显示盘上的体重读数模糊不清，用解析式求出此时的体重．

k(度)	0	72	144	216
Y(千克)	0	25	50	75

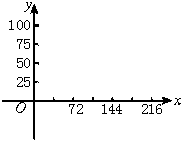
图11

参考答案

一.1.A　 2.D　 3.B　 4. D　 5.B　　6.　C　 7. B　 8. C

二. 9. 2　  10.　9×10　 11. -8　 12. 3　13.  AB＝AC（答案不唯一）

14. 200个（提示：只能是8aba8或 9aba9的形式而ab只能是00到99有100种可能，所以一共可制作200个）

15. 251, 4（提示：观察表中数据会发现，从2至5列奇数行上的数字都比前一奇数行上的数字大16.而2006=125×16+6，因此在第125×2+1=251行第4列）

16.　

三.

17.由2x-8=x+6，解得x=14.所以 正三角形边长为14+6=20.由3y+2=20，解得y=6，所以

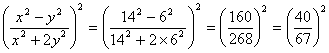于是

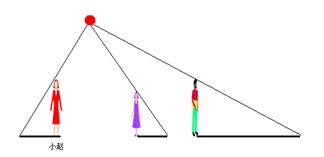
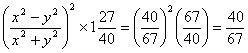
18.如图：

19.连结OC，由AB切⊙O于C，则OC⊥AB，所以在RT△OAC中由勾股定理得；

OA==

20.在△ABC中，由勾股定理可以得到，即

1500，所以BC=1200.AC+BC-AB=1200+900-1500=600（米）.

农用车的速度是18千米/时，即300米/分.行驶600米所用时间为600÷300=2，即可节约2分钟.

四.

21.只要符合题意即可。

22.共有6、5、4；6、5、3；6、5、2；6、4、3；6、4、2；6、3、2；5、4、3；5、4、2；5、3、2；4、3、2.10种 情况，可形成三角形的有6、5、4；6、5、3；6、5、2；6、4、3；5、4、3；5、4、2；4、3、2七种情况可构成三角形，所以概率为.举例略.

五.

23. （1）如图所示；

（2）①；

x	5	10	20	30	40	50
x2/y	200	200	200	200	200	200

②y=x²;

24. 第6个图为216个小正方体，规律为n

六.

25. (1)，(2)必然事件(过程略)，(3)

26. 实践一：∵　∠CED＝∠AEB，∠CDE＝∠ABE＝Rt∠，

　　∴　△CED∽△AEB．∴　．

　　∴　，∴　AB≈5.2米．

　　实践二：(1)①②　(2)示意图略　(3)CD＝a，BD＝b　(4)a＋b

七.

27. （1）由图象知，当t由0增大到4时，点P由B→C，∴4×2=8（cm）

（2）S_△ABC=×6×8=24（cm²）

（3）同理，由图象知CD=4cm，DE=6cm，则EF=2cm，AF=14cm

∴图1中图形面积为4×8+2×14=60（cm²）

（4）图1中多边形的周长为（14+6）×2=40cm  b=(40-6)÷2=17(秒)

28. (1)符合这个图形的函数解析式为：y＝kx(k＝0)．

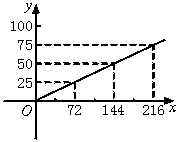
　　(2)将x＝72，y＝25代入，得25＝72k，即k＝，∴　y＝x　　　　①

　　验证：将其他两对分别代入①式，均满足．

　　∴　符合要求的函数解析式是y＝x由题意知， 0≤y≤120，0≤x≤120，解得0≤x≤345.6，即自变量x的取值范围是0≤x≤345.6．

　　(3)当x＝158.4度时，y＝·158.4＝55(千克)，即此时的体重为55千克．