2005年中考数学模拟试题（3）
一、填空题（每空3分，共36分）
1．若a、b两实数互为倒数，则ab= ．
2．如果F=
（G≠0，M≠0），那么m=
．
3．64的算术平方根是 ．
4．若代数式(2x+1)2的值为9，则x的值为 ．
5．如果方程
x2－2x+a=0有实数根，那么a的取值范围是 ．
6．在函数y=
中，自变量x的取值范围是
．
7．已知y－2与x成正比例，当x=3时，y=1，则y与x间的函数关系式为 ．
8．在Rt△ABC中，∠C=90°，BC=4，sinA=
，则AB= ．
9．等腰梯形中，上底：腰：下底=1:2:3，则下底角的度数是 ．
10．一圆中两弦相交，一弦长为2a且被交点平分，另一弦被交点分成1:4两部分，则另一弦长为 ．
11．已知
，那么m:n= ．
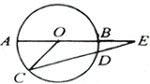
12．如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，已知AB=2DE，∠E=18°，则∠AOC的度数为
．
二、选择题（每小题3分，共36分）本题中每小题都给出代号为A、B、C、D的四个结论，其中只有一个是正确的，将正确结论的代号填在下表中，填对得3分，不填、填错及所填多于一个代号得0分．
13．当a＜0时，化简
，得（ ）
（A）－2 （B）0 （C）1 （D）2
14．一个到火星旅行的计划，来回的行程需要三个地球年（包括在火星上停留449个地球天）．已知火星和地球之间的距离为34,000,000千米，那么，这个旅行的平均速度是每小时多少千米？（说明：地球年、地球天是指在地球上一年或一天，即：一年=365天；一天=24小时）（ ）
（A）
（B）
（C）
（D）
15．已知x1和x2是方程2x2+3x－1=0的两个根，则
的值是（ ）
（A）3 （B）－3 （C）
（D）－
16．下面四个方程中，有实数解的是（ ）
（A）
（B）
（C）
（D）
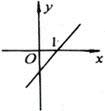
17．如图，直线l是一次函数y=kx+b的图象，则其中（ ）
（A）k＞0，b＞0 （B）k＞0，b＜0
（C）k＜0，b＜0 （D）k＜0，b＞0
18．二次函数y=－x2－2x+2的顶点坐标、对称轴分别是（ ）
（A）(1, 3), x=1
（B）(－1, 3), x=1
（C）(－1, 3), x=－1 （D）(1, 3), x=－1
19．如果一组数据x1，x2，x3，x4，x5的平均数是
，则另一组数据x1，x2+1，x3+2，x4+3，x5+4的平均数是（ ）
（A）
（B）+2 （C）+
（D）+10
20．已知sina+cosa=m，sina·cosa=n，则m、n的关系是（ ）
（A）m=n （B）m=2n+1 （C）m2=2n+1 （D）m2=1－2n
21．同一个圆的内接正六边形和外切正六边形的周长的比等于（ ）
（A）3:4 （B）
:2 （C）2:
（D）1:2
22．在△ABC中，∠A:∠B:∠C=1:2:3，CD⊥AB于D，AB=a，则DB等于（ ）
（A）
（B）
（C）
（D）
23．下列说法不正确的是（ ）
（A）以等腰三角形顶角的顶点为圆心，底边上的高为半径的圆与底边相切
（B）若两个三角形的边长为8、6、4和4
、3、2，则这两个三角形
相似
（C）梯形的中位线平行于两底，并且等于两底和的一半
（D）命题“两圆外离，则两圆无公共点”的逆命题是真命题
24．以下有四个命题：
①斜边和一锐角对应相等的两个直角三角形全等
②两圆相切时连心线必过切点
③对角线垂直且相等的四边形是平行四边形
④垂直于弦的直径平分这条弦，并且平分弦所对的两条弧
其中真命题的个数是（ ）
（A）1个 （B）2个 （C）3个 （D）4个
三、解答题（第25、26题每题5分，第27~31题每题6分，第32题8分，共48分）
25．（本题5分）解方程组：
．
26．（本题5分）已知正比例函数y=kx与反比例函数y=
的图象都过A（m,，1）点，求此正比例函数解析式及另一个交点的坐标．
27．（本题6分）已知关于x的方程x2－2x+k=0有实数根x1、x2，且y=
，试问：y值是否有最大值或最小值，若有试求出其值，若没有请说明理由．
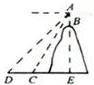28．（本题6分）如图，在一座山的山顶B处用高为1米的测倾器望地面C、D两点，测得的俯角分别为60°和45°，若已知DC的长是20米，求山高BE．（结果可用根式表示）
29．（本题6分）请找出下图圆中的圆心，并写出你找圆心的方法．（不要求证明）
30．（本题6分）某工程由甲、乙两队合做6天完成，厂家需付甲、乙两队共8700元；乙、丙两队合做10天完成，厂家需付乙、丙两队共9500元；甲、丙两队合做5天完成全部工程的，厂家需付甲、丙两队共5500元．
（1）求甲、乙、丙各队单独完成全部工程各需多少天？
（2）若工期要求不超过15天完成全部工程，问可由哪队单独完成此项工程花钱最少？请说明理由．
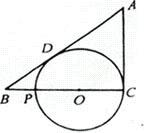31．（本题6分）如图，已如AC切⊙O于C点，CP为⊙O的直径，AB切⊙O于D与CP的延长线交于B点，若AC=PC．求证：（1）BD=2BP，（2）PC=3BP．
32．（本题8分）已知二次函数y=ax2+bx+c的图象过点A（2，4），顶点的横坐标为
，它的图象与x轴交于两点B（x1，0）、C（x2，0），与y轴交于点D，且
=13．试问：y轴上是否存在点P，使得△POB与△DOC相似（O为坐标原点）？若存在，请求出过P、B两点直线的解析式，若不存在，请说明理由．
2005年中考数学模拟试题(3)答案
1.1
2. 
3.8
4.1或－2
5.a≤3 6.x≥－
7.y=－x+2
8.6
9.60° 10.
11.
2:3
12. 54°
13.A. 14.C. 15.A. 16.D.
17.B. 18.C. 19.B. 20.C.
21.B. 22.A. 23.D. 24.C.
25.由第一个方程得x=－3y，把x=－3y代入第二个方程得(－3y)2+3y2－6y2=24，整理得y2=4，∴y1=2，y2=－2．把y1=2，y2=－2分别代入方程x=－3y，得x1=－6，x2=6．
∴
26.∵y=图象过A（m，1）点，则1=
，∴m=3，即A（3，1）．将A（3，1）代入y=kx，得k=，∴正比例函数解析式为y=x．又x=∴x=±3．当x=3时，y=1；当x=－3时，y=－1．∴另一交点为（－3，－1）．
27.∵x2－2x+k=0有实数根，∴22－4k≥0．∴k≤1．∵x1+x2=2，x1x2=k，∴y==(x1+x2)[(x1+x2)2－3x1x2] =2(4－3k)=8－6k．即y=8－6k．∵k≤1，∴－6k≥－6，∴8－6k≥8－6=2．即y有最小值为2．
28.在Rt△ACE中，有CE=AE·tg30°，在Rt△ADE中，有DE=AE·tg45°，∴DC=DE－CE=AE(tg45°－tg30°)．∴AE=
=30+10．∴BE=AE－AB=（29+10）米．
29.（1）在圆上任取三点A、B、C．（2）连AB、BC．（3）作线段AB的垂直平分线EF．（4）作线段BC的垂直平分线MN，与EF交于O点．则O点即为该圆的圆心．
30.(1)设甲队单独做x天完成，乙队单独做y天完成，丙队单独做z天完成，则
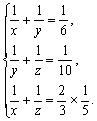解方程组，得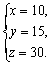
（2）设甲队做一天应付给a元，乙队做一天应付给b元，丙队做一天应付给c
元．则有
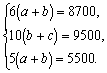解方程组，得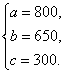
∵10a=8000（元），15b=9750（元），∴由甲队单独完成此工程花钱最少．
31.（1）连结OD，∵D、C是切点，PC是直径，OD是半径，∴∠BDO=∠ACB=90°．又∠B=∠B，∴△BDO∽△BCA，∴
∵AC=PC=2OD，∴BD=BC．①又BD2=BP·BC，②，②÷①，得BD=2BP．（2）由BD2=BP·BC，又∵BC=BP+PC，BD=2BP．
∴4BP2=BP(BP+PC)．∴4BP=BP+PC，∴PC=3BP．
32.∵y=ax2+bx+c的图象与x轴交于点B(x1,0)，C(x2,0)，∴x1+x2=－
，x1x2=
又∵
，即(x1+x2)2－2x1x2=13，∴(－)2－2·
=13．①又由y的图象过点A（2，4），顶点横坐标为，则有4a+2b+c=4，②
③解由①、②、③组成的方程组，得a=－1，b=1，c=6．∴y=－x2+x+6．与x轴交点坐标为（－2，0），（3，0）．与y轴交点D坐标为（0，6）． （4分）
设y轴上存在点P，使得△POB∽△DOC，则（1）当B（－2，0），C（3，0），D（0，6）时，有
，OB=2，OC=3，OD=6，∴OP=4．即点P坐标为（0，4）或（0，－4）．当P点坐标为（0，4）时，可设过P、B两点直线的解析式为y=kx+4，有0=－2k+4，得k=2．∴y=2x+4．当P点坐标为（0，－4）时，可设过P、B两点直线的解析式为y=kx－4．有0=－2k－4，得k=－2．∴y=－2x－4．或
，OB=2，OD=6，OC=3，∴OP=1．这时P点坐标为（0，1）或（0，－1）．当P点坐标为（0，1）时，可设过P、B两点直线的解析式为y=kx+1．有0=－2k+1，得k=．∴y=x+1．当P点坐标为（0，－1）时，可设过P、B两点直线的解析式为y=kx－1．有0=－2k－1，得k=－．∴y=－x－1．（2）当B（3，0），C（－2，0），D（0，6）时，同理可得y=－3x+9或y=3x－9或y=－x+1或y=x－1