2003年初中毕业会考（中考）数学全真试卷

A卷（100）　　　　　  教师：纪新林

题号	一	二	三	四	五	总分
得分

一、选择题（14×3分）

1、方程2x(x –3)=5(x-3)的根是（ ）

A、　B、x=3　 C、，x₂=3 D、

2、两圆半径长分别为R和r，　两圆心间的距离为d，以R，r，d为长度的三条线段首尾相接可以围成一个三角形，则两圆的位置关系是（　　）

A、外离　　　B、相切　　　　　 C、相交　　　　 D、内含

3、函数中自变量x的取值范围是 （ ）　　　　　　　 

 A、x≥-5　B、x＞-5  C、x≥-5且x≠-1 D、x≥-5且x≠±1

4、D在Rt△ABC中，∠C=90⁰，当30⁰＜A＜60⁰时，cotA的值

A、　　  B、

C、　　  D、

5、函数、y = 2x²、y = x–1的图形中，是中心对称图形，且对称中心是原点的有（ ）

A、0个　B、1个  C、2个　D、3个

6、圆内接正四边形的边长为a，外切

正四边形的边长为b，则a：b=（ ）

A、B、 C、　D、

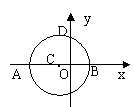
7、如图，⊙C的直径AB在x轴上，与y轴交于点D，设A的横坐标为–8，D的纵坐标为4，则⊙C的直径等于（　 ）

A、8　B、10　 C、12　 D、14

8、一名射击运动员连续射靶8次，命中的环数如下：8 9 10 9 8 7 10这名运动员射击环数的众数与中位数分别是（ ）

　　　 A． 3与8　　　B．8与8.5　　C．8.5与9　　　　　 D．8与9

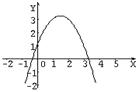9、如图, 二次函数 y＝ax²+bx+c 的图像如图所示, 则（ ）

Ａ、a＞0, b＞0　　 Ｂ、a＞0, c＞0

Ｃ、b＞0, c＞0　　Ｄ、a、b、c、都小于0

10、两根均为负数的一元二次方程是（ ）

A、7x²-12x+5=0　B、6x²-13x-5=0

C、4x²+21x+5=0　 D、2x²+15x-8=0　

11、一次函数y=kx+b的图像经过点（m，1）和（-1，m）其中m＞1则k、b应满足（ ）。

A、k＞0且b＞0　　  B、k＜0且b＞0

C、k＞0且b＜0 　　 D、k＜0且b＜0

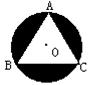
12、如图，等边三角形ABC内接于半径为1

的⊙O中，则阴影部分的面积是（ ）

A、 B、 C、D、

13、 一个圆锥粮仓顶盖半径为5米，圆锥高为米，若用铁皮做一个这样的粮仓顶盖（无底），需用铁皮

A、 B、　C、 D、

14、二次函数y=ax²+bx+c的图像只经过第一、二、三像限，则一次函数y=ax-b的图像是　

 

二、填空题（8×4分）

15、星期天上午9时小王从家中出发到距家600米处的书店买书，图（3）是9时至10时这段时间内他与家的距离随时间变化的图像。根据此图像，请你用简短的语句分别叙述小王在9时10分至9时15分与9时30分至9时50分这两段时间内活动的情况：

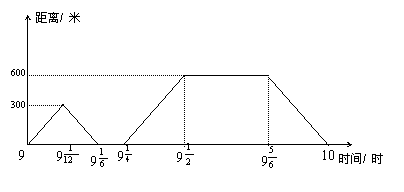9时10分至9时15分:　　　　  　　　　 。

9时30分至9时50分：　　　　　　　 

16、. △ABC的内角平分线的交点是I，设∠BIC=y⁰，∠A=x⁰，则y与x的函数关系式为　　　　,自变量x的取值范围是　　　　　  .

17、 对于一次函数y=(m+4)x+2m-1，若随增大而增大，且它的图像与轴的交点在轴下方，则m的取值范围是　　　

18、Rt△ABC中，∠C=90⁰，AB=10，AC=6，以C为圆心，5为半径作⊙C，则⊙C与AB的位置关系是　　　　　　　　 

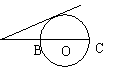19、写出一个只含字母x的代数式（要求：（1）要使此代数式有意义，字母x必须取全体正数；（2）此代数式的值恒为负数）：　　　　　　　　　  。

20、如图，△ABC的外接圆⊙O的

半径为2cm,∠A=30°，则BC=　　cm　　

21、正方形ABCD与正六边形EFGHMN的周长相等，则正方形ABCD的外接圆与正六边形EFGHMN的外接圆半径之比为__________。

22、点A在抛物线y =2x ²+6 x -1的对称轴上，则点A的坐标是　　

（写出符合条件的一个即可）

三、作图题（5分，不写画法，保留痕迹）

23、已知：△ABC；求作：⊙O，使点O在线段AB上，并且⊙O与AC、BC都相切。(保留作图痕迹，不要求写作法、证明讨论)

　四、解答题（3×7分）

24、 如图，我省201道的横断面为等腰梯形ABCD，斜坡AB的坡度为1：，路面宽5米，路高4米，求：（1）路基宽多少米？

（2）修一段500米的路需土石方多少立方米？（精确到十分位）

25、如图,P是反比例函数图像一分支上任意一点，求矩形PMON的面积S时，可设点P的坐标为（x，y），∵，

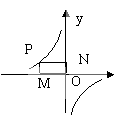∴xy=-6，∴ S_矩形PMON=PM·PN=y·x=xy=-6=6若设P为反比例函数（k≠0）的图像一分支上任意一点，则矩形PMON的面积S等于多少？证明你的结论。

　　

26、已知方程4x²-2(m+1)x+m=o 的两根恰好是一个锐角三角形两锐角的余弦值，试求m.

B卷（50分）

五、解答题（共50分）

27、（8分）已知一次函数y=kx+b(k＜0)的图像经过P(0，-12)，且直线与两条坐标轴围成的三角形面积为24，求这个一次函数的解析式。

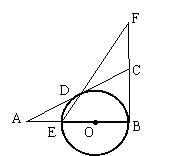28、（8分）在△ABC中，∠B=90⁰，O是AB上一点，以O为圆心，OB 为半径的圆与AB交于E，与AC切于点D，直线ED交BC的延长线于F。　 1、求证：BC=FC

2、若AD∶AE=2∶1求cot∠F的值

29、（8分）小张将自己参加工作后第一次工资收入400元钱，按一年定期存入银行，到期后，小张支取了200元钱捐给希望工程，剩下的200元钱和应得的利息全部按一年定期存入银行。若存款年利率保持不变，到期后可得本金和利息共212.16元。求这种存款方式的年利率

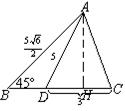
30、（9分）已知，如图，△ABC ∠B=45⁰，,

D是BC上一点， 的度数及AC的长。

31、（9分）（在下面的（Ⅰ）（Ⅱ）两题中选做一题，若两题都做，按（Ⅰ）题评分）

Ⅰ、如图，已知抛物线y=-x²+ax+b与x轴从左到右交于A、B两点，与y轴交于C点，且∠BAC=α，∠ABC=β，tanα- tanβ=2，

∠ACB=90⁰。（1）求点C的坐标；（2）求抛物线的解析式；

（3）若抛物线的顶点为P，求四边形ABPC的面积。

　  　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

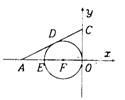Ⅱ、已知，如图，Rt△AOC中，直角边OA在x轴负半轴上，OC在y轴正半轴上，点F在AO上，以F为圆心的圆与y轴、AC边相切，切点分别为O、D，⊙F与x轴的另一个交点为E，若，OF的半径为。(1)求过A、C两点的一次函数的解析式；(2)求过E、D、O三点的二次函数的解析式；(3)证明(2)中抛物线的顶点在直线AC上。

32、（8分）如图，两个半径为r的等圆⊙O₁与⊙O₂相切于点P。

（1）操作、观察：将三角板的直角顶点放在P点，并将三角板绕点P旋转，使三角板的一边PA与⊙O₁相交于点A，另一边PB与⊙O₂相交于点B，连接AB，在三角板绕点P旋转的过程中，线段AB的长是否改变？它与半径r之间有什么关系？

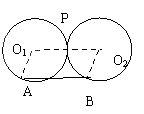（2）证明你所得的结论。

（1）解：在运动过程中，线段AB的

大小　　　　　　　 ，且AB=　　　

（2）证明：连结O₁A、O₂B和O₁ O₂。