（1）初三数学中考模拟题一
班级______姓名_________得分________
一、填空题（共36分，每小题2分）
1、 －2 的相反数是（ ）
2. 计算(2－1)2,结果等于（ ）
3、如果2(x＋3)的值与3(1－x)的值互为相反数，那么x等于（ ）
4、已知等腰三角形的一边等于3，一边等于6，则它的周长等于（ ）
5．函数y=
+ 2的自变量x的取值范围是＿＿＿＿＿。
6．分解因式：4x2-y2=＿＿＿＿＿＿＿＿。
7．如图，弧AB的度数为600，那么圆周角∠ACB＝＿＿＿。
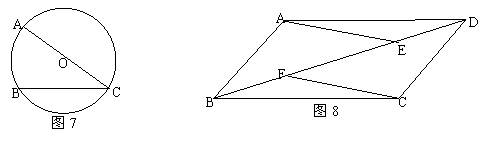
8．如图，在平行四边形ABCD中，BD是对角线，E、F是对角线上的两点，要使△BCF≌△DAE，还需添加一个条件（只需添加一个条件）是＿＿＿＿＿＿＿＿＿＿＿＿＿。
 |
9、已知梯形的上底长为3cm，下底长为7cm，则此梯形中位线长为＿＿＿＿＿＿＿cm.
10、在半径为9cm的圆中，600的圆心角所对的弧长为＿＿＿＿＿＿cm.
11、 计算：
12、用反证法证“垂直于同一条直线的两条直线平行”的第一步是 。
13、某种储蓄的月利率是0.2%，存入100元本金，本息和y（元）与所存月数x之间的函数关系式为 ，若获利不少于8元，至少应存 个月。
14、方程
的根是__________
15、如果关于x的多项式
在实数范围内能分解因式，那么k的取值范围是________
16、如果一传送带和地面所成斜坡的坡度为1︰2，它把物体从地面送到离地面9米的地方，那么物体所经过的路程为_____米
17、值：tg60°·tg45°－cos30° + 1=____________
18、 △ABC中，如果∠A=60°，∠B的度数是∠A与∠C的度数的比例中项，那么△ABC是__________三角形。
二、选择题（共27分，每小题3分）
1、第二十届电视剧飞天奖今年有a部作品参赛，比去年增加了40%还多2部。设今年参赛的作品有b部，则b是（ ）
A.
B.a(1＋40%)＋2
C.
D.a(1＋40%)－2
2、a＞b，则下列不等式一定成立的是（ ）
A.
＜1 B.
＞1
C.－a＞－b D.a－b＞0
3、下列各式与
是同类二次根式的是（ ）
A.
B.
C.
D.
4、第一季度我国增值税、消费税比上年同期增收3.07×1010元，也就是说增收了（ ）
A.30.7亿元 B.307亿元
C.3.07亿元 D.3070亿元
5、面不等式组无解的是：（ ）
A.
B
C.
D.
6、 化简二次根式a的结果是（ ）
A.
B.－
C.
D.－
7、我国最长的河流长江全长约为6300千米，用科学计数法表示为（ ）
A.63×102千米 B.6.3×102千米
C. 6.3×103千米 D. 6.3×104千米
8、面运算正确的是（ ）
A.(－2x2)·x3=4x6 B.x2÷x=x
C.(4x2)3=4x6 3x2－(2x2)2=x2
9.下列命题正确的是 （ ）
A、对角线相等的四边形是矩形 B、相邻的两个角都互补的四边形是平行四边形
C、平分弦的直径垂直于弦，并且平分弦所对的两条弧 D、三点确定一个圆
三、作图与计算题：
1、(本小题5分)
已知线段a、b，求作线段x，使 a：b=b：x.
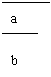
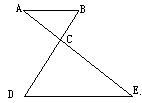
2. (本小题5分)
如图，AB∥DE,AC=4,BD=9,CD=6.
求CE的长.
四、解答题：
1、(本小题6分)
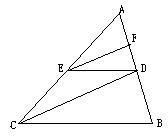
如图，在△ABC中，EF∥CD,DE∥BC.求证：
AF：FD=AD：DB.
(本小题6分)
2、 文具店出售书包和文具盒，书包每个定价30元，文具盒每个定价5元，该店制定了两种优惠方案：①买一个书包赠送一个文具盒。②按总价九折付款。某班需购8个书包，文具盒若干（不少于8个）如果设购文具盒数为x（个），付款为y（元）；
（1） 分别求出两种优惠方案中y与x之间的函数关系式；
（2） 若购文具盒60个，两种方案中哪一个更省钱？
3、(本小题6分)
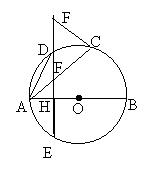
如图，AB、AC分别是⊙O的直径和弦，D为劣弧AC上一点，DE⊥AB于点H，交⊙O于点E，交AC于点F，P为ED的延长线上一点。
(1)当△PCF满足什么条件时，PC与⊙O相切，为什么？
（2）当点D在劣弧AC的什么位置时，才能使AD2=DE·DF，为什么？
(本小题9分)
4．
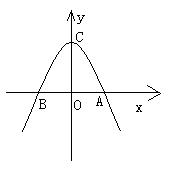
知抛物线
与x轴有两个交点A、B，点A在x轴的正半轴上，点B在x轴的负半轴上，且OA=OB。
（1） 求m的值；
（2）求抛物线的解析式，并写出抛物线的对称轴和顶点C的坐标；
（3）问在抛物线上是否存在一点M，使△MAC≌△OAC，若存在，求出点M的坐标；若不存在，请说明理由。
