2004年深圳市数学中考试题
| 题号 | 一 | 二 | 三 | 总 分 | |||||
| 1-10 | 11-15 | 16 | 17 | 18 | 19 | 20 | 21 | ||
| 得分 | |||||||||
(说明:本试卷考试时间为90分钟,满分为100分)
一、选择题:(本题共10小题,每题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
每题给出4个答案,其中只有一个是正确的,请把选出的答案编号填在上面的答题表中,否则不给分.
1、16的平方根是
A、4 B、-4 C、±4 D、±2
2、下列等式正确的是
A、(-x2)3= -x5 B、x8÷x4=x2 C、x3+x3=2x3 D、(xy)3=xy3
3、不等式组![]() 的解集在数轴上的表示正确的是
的解集在数轴上的表示正确的是
 |
A B

C D
4、已知⊙O1的半径是3,⊙O2的半径是4,O1O2=8,则这两圆的位置关系是
A、相交 B、相切 C、内含 D、外离
5、学校开展为贫困地区捐书活动,以下是八名学生捐书的册数:2,2,2,3,6,5,6,7,则这组数据的中位数为
A、2 B、3 C、4 D、4.5
6、下列图中:①线段;②正方形;③圆;④等腰梯形;⑤平行四边形
是轴对称图形,但不是中心对称图形有
A、1个 B、2个 C、3个 D、4个
7、函数y=x2-2x+3的图象顶点坐标是
A、(1,-4) B、(-1,2) C、(1,2) D、(0,3)
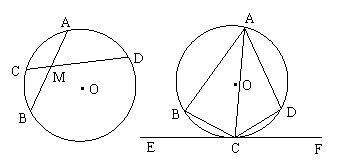
8、如图,⊙O的两弦AB、CD相交于点M,AB=8cm,M是AB的中点,CM:MD=1:4,则CD=
A、12cm B、10cm C、8cm D、5cm
9、圆内接四边形ABCD中,AC平分∠BAD,EF切圆于C,若∠BCD=120º,则∠BCE=
 A、30º
B、40º
C、45º
D、60º
A、30º
B、40º
C、45º
D、60º
 |
(8) (9) (10)
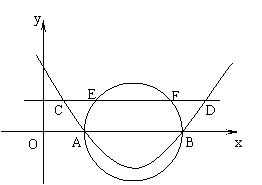
10、抛物线过点A(2,0)、B(6,0)、C(1,![]() ),平行于x轴的直线CD交抛物线于点C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是
),平行于x轴的直线CD交抛物线于点C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是
A、2 B、4 C、5 D、6
二、填空题:(共5小题,每题3分,共15分)
11、分解因式:x2-9y2+2x-6y=______.
12、在函数式y=![]() 中,自变量x的取值范围是_______.
中,自变量x的取值范围是_______.
13、计算:3tan30º+cot45º-2tan45º+2cos60º=_______.
14、等腰三角形的两边长分别为2cm和5cm,则它的周长为________.
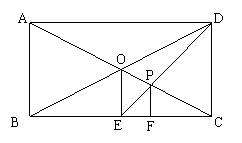
15、在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连结DE交AC于点P,过P作PF⊥BC,垂足为F,则![]() 的值是_____.
的值是_____.
 |
三、解答题:(本部分共6题,其中第16题7分,第17-18题各8分,第19-20题各10分,第21题12分,共55分)
16、计算:1-![]() +
+![]() +(π-
+(π-![]() )0 (7分)
)0 (7分)
17、解方程组:![]() (8分)
(8分)
18、在深圳“净畅宁”行动中,有一块面积为150亩的绿化工程面向全社会公开招标。现有甲、乙两工程队前来竞标,甲队计划比规定时间少4天,乙按规划时间完成。甲队比乙队每天多绿化10亩,问:规定时间是多少天?(8分)
19、已知x1、x2是关于x的方程x2-6x+k=0的两个实数根,且x12x22-x1-x2=115,
(1)求k的值;(7分)
(2)求x12+x22+8的值. (3分)
20、等腰梯形ABCD中,AB//CD,AD=BC,延长AB到E,使BE=CD,连结CE
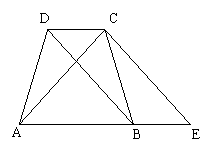 (1)求证:CE=CA;(5分)
(1)求证:CE=CA;(5分)
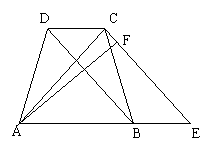 (2)上述条件下,若AF⊥CE于点F,且AF平分∠DAE,
(2)上述条件下,若AF⊥CE于点F,且AF平分∠DAE,![]() ,求sin∠CAF的值。(5分)
,求sin∠CAF的值。(5分)
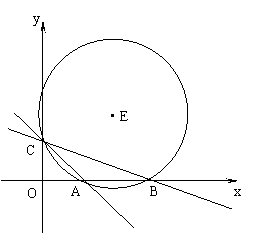
21、直线y= -x+m与直线y=![]() x+2相交于y轴上的点C,与x轴分别交于点A、B。
x+2相交于y轴上的点C,与x轴分别交于点A、B。
(1)求A、B、C三点的坐标;(3分)
(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(4分)
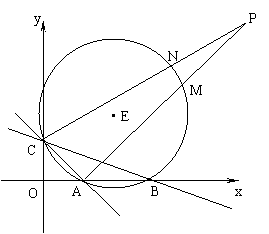
 (3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离(可用含θ的三角函数式表示)。(5分)
(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离(可用含θ的三角函数式表示)。(5分)
参考答案
1-10、CCDDC ACBAB
11、(x-3y)(x+3y+2)
12、x≥-1,且x≠1
13、![]()
14、12cm
15、![]()
16、![]()
17、![]() ,
,![]()
 18、
18、![]() 设规定时间为x天,
设规定时间为x天,![]() ,x=10
,x=10
19、(1)k=-11;(2)66
20、(1)略;(2)![]()
21、(1)(2,0),(2![]() ,0),(0,2)
,0),(0,2)
(2)30º;(![]() ,
,![]() );2
);2![]()
(3)可自己先推证一个事实:
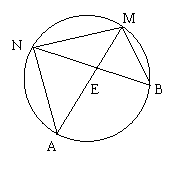
 如图所示:MN为⊙E中任一弦,它对的圆周角为∠B,AM为直径,则∠ANM为直角,则sinB=sinA=
如图所示:MN为⊙E中任一弦,它对的圆周角为∠B,AM为直径,则∠ANM为直角,则sinB=sinA=![]()
即MN=AM·sinA (*)(其实就是正弦定理)

![]() 这是本题的解题的理论基础。
这是本题的解题的理论基础。
(I)当点P在⊙E外时,如图
连接AN,
则∠MAN=∠ANC-∠P=∠ABC-∠P
=30º-θ
由(*)得:MN=4![]() sin(30º-θ)
sin(30º-θ)
(II)当P在⊙E内时
同理可得:MN=4![]() sin(θ-30º)
sin(θ-30º)
其它情况研究方法相同。
