浮力（二）——典型题解法举例

　　浮力是初中物理力学中，也是全部初中物理中最复杂，最灵活的一部分，有的题还有一些特殊的简便的方法.但是，归根结底就是那么几个关系，解题时只要列清这几个关系式，问题就基本理清了.比如，受力分析和平衡关系；浸入部分的体积和物体的总体积；物体密度和浸入的液体的密度.
　 当然，首先要搞清题中所描述的物理状态，搞清题目所求的是哪些量，然后，要画出受力分析图.
　 这里就举出一些典型题，并以分析它们的方法作为范例.
　 例1、如图1所示，底面积为20厘米²，上下等粗的烧杯中的水面上浮着一质量为80克的木块，木块上放着一个23.4克的铁块，木块上表面恰好全部浸入水中，若把铁块直接放入(ρ_铁=7.8×10³千克/米³，g=10牛/千克)

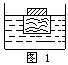
求：(1)水面下降多少厘米？
(2)水对容器底部的压强改变了多少？
　　分析：液面的升降和木块排开的水的体积有关.而排开水的多少又直接和物体在水中的状态有关.比如，当铁块放在木块上时，整体漂浮，这时浮力等于重力，即F_浮=G_木+G_铁，可是当铁块投入水中时，铁块除受浮力、重力，还受底面的支持力，这个支持力就是刚才减少的浮力.反过来，由浮力的变化，可以推出排开水的体积，进而推出水面的变化和水对容器底的压强.
　　解：令铁的体积为V_T，∴，浮力减少的量为△F_浮=G-F_浮T=0.204牛

水面降底的高度为
底面受水压强变化△P=ρ_水g△h=10³×10×1.02×10^-2帕=102帕
　　例2、一块边长是0.1米的正方体木块，在水中最多能托起7.0牛、密度为7.0×10³千克/米³的铁块而不致下沉，则木块的密度是多少？
　　分析：本题在浮力题中并不复杂，但它的困难之处在于“不下沉”三字，也就是物体什么时候受水的浮力最大？是木块刚刚没入水中时，还是铁块刚刚全部没入水中时？从题意分析，应是后者.见图2

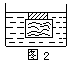解：根据平衡关系G_木+G_铁=F_浮
有ρ_木gV_木+ρ_铁gV_铁=ρ_水g(V_木+V_铁)
∵

答：木块的密度为0.4×10³千克/米³.
例3、如图3所示，水槽中装有一定量的水，将一只装有铁块的塑料盒放入水中，此时，水槽底部受到水的压强是P₁，将铁块从盒中取出后直接放入水槽中，水对水槽底部的压强为P₂，若P₁-P₂=490帕，水槽的底面积为2分米²，铁的密度是7.8×10³千克/米³，则（ ）
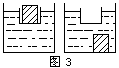　　A.水面下降了5厘米
　　B.塑料盒受到的浮力减小了9.8牛
　　C.铁块受到的水槽的支持力是9.8牛
　　D.铁块质量约1.75千克
　　分析：已知条件△P=P₁-P₂=490帕使我们了解了哪些情况，又可以推导出哪些情况呢？
∵P=ρgh，∴△P=ρg△h ，即有可以求得水面变化了多少.而∵F=PS有△F=△PS，而底面受的支持力N=△F=△PS.
　　再从金属块受力分析，支持力和浮力等于其重力，N=ρ_金gV_金-ρ_水gV_金=（ρ_金-ρ_水）gV_金，可求出V_金进而求出m_金.
　 解：(1)∵P=ρgh，∴
　　(2)N=△F=△P·S=490帕×2×10^-2米²=9.8牛
　　(3)∵N=G-F_浮=ρ_金gV_金-ρ_水gV_金=（ρ_金-ρ_水）gV_金
　 ∴V_金=0.25×10^-3米³ ，m_金=ρ_金V_金=1.25千克.
　　正确的选择是A、C、D.
　　例4、一个体积为0.2分米³的铁球，密度为7.8×10³千克/米³.用一根细绳与木块连接在一起，如图4所示，木块的密度0.5×10³千克/米³，体积为5分米³，若不断向容器内注水，求：

　
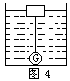
(1)当水浸没木块的体积为3分米³时木块能保持静止，求绳的拉力.
(2)继续向容器内注水，木块浸入水中的体积至少为多大时，铁球对容器底没有压力？
　 分析：首先要判明状态，找到物体平衡时各个力的关系.结合图我们可以判断出，木块此时漂浮，它受向上的浮力和向下的重力、拉力.浮力的大小由浸入水中的体积决定了，重力由自身的体积和密度可以算出.进而由平衡关系F_浮=G+T（T为绳子给的拉力），可以求出T.我们分析时，把木块和铁球看做有联系又互相独立的两个物体，它们之间的联系，就是铁球给木块的拉力等于木块给铁球的拉力，这是作用力和反作用力的关系.此时铁球的状态无须管，但是，随着木块浸入水中体积的增加，T=F_浮木-G_木 增大，铁球受的拉力T′=G_铁-N也增大（N为铁球受的底面支持力），直到这拉力T′等于球的重力时，底面支持力为零.
解：(1)G_木+T=F_浮木，
T=F_浮木-G_木=ρ_水gV_排木-ρ_木gV_木=4.9牛
(2)对铁球和木块整体受到的浮力应和它们的重力平衡，F_浮木+F_浮铁=G_木+G_铁
ρ_水gV_排木′+ρ_水gV_球=ρ_木gV_木+ρ_铁gV_铁
解得： V_排木′=3.86×10^-3米³
　 例5、将一个木块放入水中，它露出水面部分的体积是24厘米³，将露出水面部分截去后放入水中，它露出水面部分体积为16厘米³，求木块总体积和它的密度.见图5
　 分析：本题关键仍是找到两种状态下，处于平衡关系的各个量，列出方程.比如在第一种情况下，设木块总体积为V，则V_排=V-24×10^-6米³.截去24厘米³后，木块体积为V-24×10^-6米³，而它浸入水中部分改为V-40×10^-6米³.

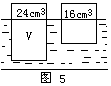
解：∵F_浮1=G₁
∴ρ_水g(V-24×10^-6米³)=ρ_木gV (1)
又∵ F_浮2=G₂
∴ ρ_水g(V-40×10^-6米³)=ρ_木(V-24×10^-6米³)g （2）
解得：8V=576cm³ 解得V=72cm³.
代入(1)
例6、质量相等的甲乙两球其密度之比为3∶2，所受浮力之比为4∶5，求ρ_乙.
　 分析，首先判断状态.它们的状态可能是两个都漂浮；一浮一沉；两球都沉，4种情况.质量相等，若漂浮，所受浮力之比应为1∶1.若两个都沉没，它们既然密度之比为3∶2，体积之比应为2∶3，浮力之比也应为2∶3.只可能一沉一浮，这时当然是密度大的沉，密度小的浮，即甲沉乙浮.
　 解：解题时，根据所求和有关的公式，都用甲的物理量来代，最后消掉，即可得出结果.

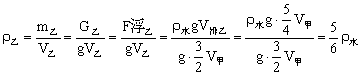
例7、一实心小球分别放入盛有足够多的水和酒精的容器中，小球受到的浮力分别为0.9牛和0.8牛.已知水和酒精的密度之比为5∶4，求小球的密度.见图6
　 分析：首先确定状态.如果小球在水中和酒精中都漂浮，那么它们受到的浮力应相等.必然是一沉一浮，显然应在密度小的酒精中沉，解题过程中，还是要把相关的物理量都推导到与水或都推导到与酒精相联系的量上去，彼此建立了联系，就可以运算了.

解：设定小球在酒精中沉淀，则V_球=V_排酒，根据阿基米德原理：

例8、如图7所示的容器内盛有空气，活塞可左右移动且不漏气，容器中有一球A，当用力F向左推动活塞时，下列说法中正确的是（ ）

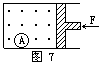
　　A.木球A对容器的压力将增大
　　B.木球A对容器的压力将减小
　　C.木球A对容器的压力将不变
　　D.无法比较木球A对容器压力的大小
　　分析：当活塞向左移动时，容器内空气体积将被压缩而减小，而它的质量不变，因而空气的密度将增大.球在容器中受到重力、浮力和底面支持力的作用.当空气密度增大时，球受的浮力变大，球重力不变，受到的支持力将变小.
　　由前面的分析，空气密度增大，F_浮=ρ_气gV_球 浮力将增大，木球A对容器的压力将减小.正确的选择是B。