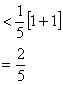数列检测

一、选择题

1.在等差数列中，若++++=120，则2-的值为　　　 （　 ）

A、20　　　 　B、22　　　　 C、24　　　　　  D、28

2.在等比数列{a_n}中，首项a₁<0，则{a_n}是递增数列的充要条件是公比q满足　 （　 ）

　A．q>1　　　　　  B．q<1　　　　　  C．0<q<1　　　　 D．q<0

3. 已知等差数列的公差为2,若成等比数列, 则=　　　　　　  （　 ）

　　　(A) –4　　　　  (B) –6　　　　(C) –8　 　 (D) –10

4.等比数列中， ，则的前4项和为　　　　　　　  （　　）

A．　81　　　 　　B．　120　　　　　 C．168　　　　　　 D．　192

5.已知数列，那么“对任意的，点都在直线上”是“ 为等差数列”的　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A. 必要而不充分条件B. 充分而不必要条件C. 充要条件D. 既不充分也不必要条件

6.设S_n是等差数列的前n项和，若　　　　　　　　　 （　　）

　　A．1　　　　　　B．－1　　　　　　　C．2　　　　　　　D．

7.正项等比数列｛a_n｝与等差数列｛b_n｝满足且，则，的大小关系为　　　　　　　　　　　　　  　　　　　　　　　　　　　　　（　 ）

　 （A） = （B）＜ （C）＞（D）不确定

8.给定正数p,q,a,b,c，其中p¹q，若p,a,q成等比数列，p,b,c,q成等差数列, 则一元二次程bx²－2ax+c=0 　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　A．无实数根　　　 　　　　　　　　 B．有两个相等的实数根

　C．有两个同号的相异的实数根　 　　 D．有两个异号的相异的实数根

9.已知等差数列的前n项和为，若m>1，且，则m等于　　　　　　　（　　）

　　A．38　　　　　　 B．20　　　　　　C．10　　　　　　　D．9

10.北京市为成功举办2008年奥运会，决定从2003年到2007年5年间更新市内现有全部出租车，若每年更新的车辆数比前一年递增10%，则2003年底更新车辆数约为现有总车辆数的（参考数据1.1⁴=1.46　1.1⁵=1.61）　　　　（　　）

　　A．10%　　　　　　B．16.4%　　　　 C．16.8%　　　　　 D．20%

二、填空题

11.设数列{a_n}满足a₁=6，a₂=4，a₃=3，且数列{a_n+1－a_n}（n∈N^*）是等差数列，求数列{a_n}的通项公式__________________.

12.已知等比数列及等差数列，其中，公差d≠0．将这两个数列的对应项相加，得一新数列1，1，2，…，则这个新数列的前10项之和为_________________.

13.设{a_n}是首项是1的正项数列, 且 0(n＝1.2,3,…),则它的通项公式＝ ______________.

14. 已知，把数列的各项排成三角形状；

　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　  　 　　

　　　　　  　　　　　　　　　　　　　　　 　　

　　　　　　　　　　　　　　　　　　　　　  ……

　 记A（m,n）表示第m行，第n列的项，则A（10，8）=　　　　  .

三、解答体

15.设是一个公差为的等差数列，它的前10项和且，，成等比数列。（1）证明；（2）求公差的值和数列的通项公式.

16. 已知等比数列的各项为不等于1的正数，数列满足，y₄=17, y₇=11

(1)证明：为等差数列；

（2）问数列的前多少项的和最大，最大值为多少？

 17.已知数列是等差数列，且

　 （Ⅰ）求数列的通项公式；

　 （Ⅱ）令求数列前n项和的公式.

18. 假设你正在某公司打工，根据表现，老板给你两个加薪的方案：

　 （Ⅰ）每年年末加1000元； （Ⅱ）每半年结束时加300元。请你选择。

　 （1）如果在该公司干10年，问两种方案各加薪多少元？

　 （2）对于你而言，你会选择其中的哪一种？

19. 已知数列，且,　 , 其中k=1,2,3,…….

（Ⅰ）求，（II）求通项公式.

20. 已知点P_n(a_n,b_n)都在直线：y=2x+2上，P₁为直线与x轴的交点，数列成等差数列，公差为1.（n∈N₊）

（1）求数列，的通项公式；

（2）若f(n)=　 问是否存在k,使得f(k+5)=2f(k)－2成立；若存在，求出k的值，若不存在，说明理由。

（3）求证：　　  （n≥2，n∈N₊）

参考答案

一、选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	C	C	B	B	B	A	B	A	C	B

二、填空题

11. （n∈N^*）　 12.978　　 13.　　　14.

三、解答题

15. 证明：因，，成等比数列，故，而是等差数列，有，,于是 ，即，化简得

（2）解：由条件和，得到，由（1），，代入上式得，故 ，，

16. （1）

y

 ∴

(2)y　　∴3d=－6　　　 d=－2　　 y

当n=12时，S有最大值144.

∴前12项和最大为144.

17.(Ⅰ）解：设数列公差为，则 又所以

（Ⅱ）解：令则由得

　　①　

②

　　当时，①式减去②式，得

 

　　所以

当时,

综上可得当时,；当时，

18. 设方案一第n年年末加薪a_n，因为每年末加薪1000元，则a_n=1000n；

设方案二第n个半年加薪b_n，因为每半年加薪300元，则b_n=300n；

(1)在该公司干10年(20个半年)，方案1共加薪S₁₀=a₁＋a₂＋……＋a₁₀=55000元。

方案2共加薪T₂₀=b₁＋b₂＋……＋b₂₀=20×300＋=63000元；

(2)设在该公司干n年，两种方案共加薪分别为：

S_n=a₁＋a₂＋……＋a_n=1000×n＋=500n²＋500n

T_2n=b₁＋b₂＋……＋b_2n=2n×300＋=600n²＋300n　 令T_2n≥S_n即：600n²＋300n>500n²＋500n，解得：n≥2，当n=2时等号成立。

∴如果干3年以上(包括3年)应选择第二方案；如果只干2年，随便选；如果只干1年，当然选择第一方案。　　　　　　　　　　　　　　　　　　　　　 

19. （I）a₂=a₁+(－1)¹=0,a₃=a₂+3¹=3. a₄=a₃+(－1)²=4, a₅=a₄+3²=13,  所以，a₃=3,a₅=13.

　 (II)  a_2k+1=a_2k+3^k = a_2k－1+(－1)^k+3^k, 所以a_2k+1－a_2k－1=3^k+(－1)^k,　同理a_2k－1－a_2k－3=3^k－1+(－1)^k－1,

　 ……a₃－a₁=3+(－1).

 所以(a_2k+1－a_2k－1)+(a_2k－1－a_2k－3)+…+(a₃－a₁)=(3^k+3^k－1+…+3)+[(－1)^k+(－1)^k－1+…+(－1)],

 由此得a_2k+1－a₁=(3^k－1)+[(－1)^k－1],于是a_2k+1=

 a_2k= a_2k－1+(－1)^k=(－1)^k－1－1+(－1)^k=(－1)^k=1  

{a_n}的通项公式为： 当n为奇数时，a_n­= 当n为偶数时，

20. 1) P　　∴　∴　

(2)

若k为奇数　　　　　　　  　　 若k为偶数

则f(k)=　　　　　　  则f(k)=2k－2

f(k+5)=b　　　　　  f(k+5)=k+3

2k+8=2k－4－2　　　　　　　　 k+3=4k－4－2

 无解：　　　　　　　　　　　　 q=3k

这样的k不存在　　　　　　　　 k=3(舍去)无解

（3）

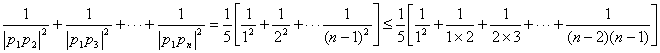=　　 n