圆锥曲线(二) ----(直线与圆锥曲线的位置关系)
班级_________ 姓名__________
1.设抛物线![]() 与过焦点的直线交于
与过焦点的直线交于![]() 两点,则
两点,则![]() 的值
( )
的值
( )
A![]()
![]() B
B![]()
![]() C.
C.![]() D
D![]()
![]()
2.直线![]() 与曲线
与曲线![]() (
)
(
)
A.没有交点 B.有一个交点 C.有两个交点 D.有三个交点
3.已知对![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 恒有公共点,则实数
恒有公共点,则实数![]() 的取值范围是
( )
的取值范围是
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
4.若双曲线![]() 的右支上一点
的右支上一点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() 的值为
的值为
A![]() -
-![]() B
B![]()
![]() C
C![]() ±
±![]() D
D![]() ±2
( )
±2
( )
5.已知双曲线中心在原点且一个焦点为![]() 直线
直线![]() 与其相交于
与其相交于![]() 两点,
两点,![]() 中点的横坐标为
中点的横坐标为![]() ,则此双曲线的方程是
( )
,则此双曲线的方程是
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
6.椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,过原点与线段
两点,过原点与线段![]() 中点所在直线的斜率为
中点所在直线的斜率为![]() ,则
,则![]() 的值是
( )
的值是
( )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
7.抛物线![]() 截直线
截直线![]() 得弦
得弦![]() ,若
,若![]() ,
,![]() 是抛物线的焦点,则
是抛物线的焦点,则![]() 的周长等于__________.
的周长等于__________.
8.直线![]() ,以椭圆
,以椭圆![]() 的焦点为焦点作另一椭圆与直线
的焦点为焦点作另一椭圆与直线![]() 有公共点且使所作椭圆长轴最短时,公共点坐标是___________.
有公共点且使所作椭圆长轴最短时,公共点坐标是___________.
9.在抛物线y2=4x上恒有两点关于直线y=kx+3对称,求k的取值范围.
10.已知椭圆的两个焦点分别为![]() ,离心率
,离心率![]() .
.
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且组段
,且组段![]() 中点的横坐标为
中点的横坐标为![]() ,求直线
,求直线![]() 倾斜角的取值范围
倾斜角的取值范围![]()
11.已知中心在原点,顶点![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() 的双曲线经过点
的双曲线经过点![]() .
.
(1)求双曲线的方程;
(2)动直线![]() 经过
经过![]() 的重心
的重心![]() ,与双曲线交于不同的两点
,与双曲线交于不同的两点![]() ,问是否存在直线
,问是否存在直线![]() 使
使![]() 平分线段
平分线段![]()
![]() 试证明你的结论
试证明你的结论![]()
12.(2006湖南卷)已知椭圆![]() :
:![]() ,抛物线
,抛物线![]() :
:![]() ,且
,且![]() 、
、![]() 的公共弦
的公共弦![]() 过椭圆
过椭圆![]() 的右焦点.
的右焦点.
(1)当![]() 轴时,求
轴时,求![]() 的值,并判断抛物线
的值,并判断抛物线![]() 的焦点是否在直线
的焦点是否在直线![]() 上;
上;
(2)若![]() 且抛物线
且抛物线![]() 的焦点在直线
的焦点在直线![]() 上,求
上,求![]() 的值及直线
的值及直线![]() 的方程.
的方程.
BDCBDA 7、![]() 8、
8、![]()
9、设B、C关于直线y=kx+3对称,直线BC方程为x=-ky+m代入y2=4x得:
y2+4ky-4m=0, 设B(x1,y1)、C(x2,y2),BC中点M(x0,y0),则
y0=(y1+y2)/2=-2k。x0=2k2+m,
∵点M(x0,y0)在直线上。∴-2k(2k2+m)+3,∴m=-![]() 又BC与抛物线交于不同两点,∴⊿=16k2+16m>0把m代入化简得
又BC与抛物线交于不同两点,∴⊿=16k2+16m>0把m代入化简得![]() 即
即![]() ,
,
解得-1<k<0
10、分析:由焦点坐标可知![]() , 由离心率可求
, 由离心率可求![]()
![]()
解:(Ⅰ)设椭圆方程为![]()
![]()
由已知,![]() ,由
,由![]() 解得a=3,
解得a=3,![]()
∴![]() 为所求
为所求
(Ⅱ)解法一:设直线l的方程为y=kx+b(k≠0)
解方程组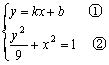
将①代入②并化简,得![]()
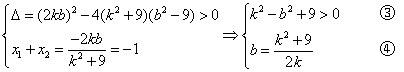
将④代入③化简后,得![]()
![]() 解得
解得![]()
∴![]()
解法二:(点差法)设![]()
![]() 的中点为
的中点为![]() 在
在
椭圆![]() 内,且直线l不与坐标轴平行
内,且直线l不与坐标轴平行![]()
因此,![]() ,
,![]()
∵![]() ,
,![]()
∴两式相减得 ![]()
即 ![]()
∴![]()
![]()
11、(I)设所求的双曲线方程为![]()
![]() 且双曲线经过点
且双曲线经过点![]() ,所以所求所求的双曲线方程为
,所以所求所求的双曲线方程为![]()
![]()
(II)由条件![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 点坐标为
点坐标为![]()
假设存在直线![]() 使
使![]() 平分线段
平分线段![]() 设
设![]() 的坐标分别为
的坐标分别为![]()
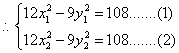
![]() 得
得![]()
![]()
又![]() 即
即![]()
![]() 的方程为
的方程为![]() 由
由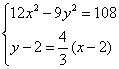
消去![]() 整理得
整理得![]()
![]() 所求直线不存在
所求直线不存在![]()
12、(Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为
x=1,从而点A的坐标为(1,![]() )或(1,-
)或(1,-![]() ).
).
因为点A在抛物线上,所以![]() ,即
,即![]() .
.
此时C2的焦点坐标为(![]() ,0),该焦点不在直线AB上.
,0),该焦点不在直线AB上.
(Ⅱ)解法一 当C2的焦点在AB时,由(Ⅰ)知直线AB的斜率存在,设直线AB的方程为![]() .
.
由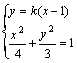 消去y得
消去y得![]() .
……①
.
……①
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=![]() .
.
 因为AB既是过C1的右焦点的弦,又是过C2的焦点的弦,
因为AB既是过C1的右焦点的弦,又是过C2的焦点的弦,
所以![]() ,且
,且
![]() .
.
从而![]() .
.
所以![]() ,即
,即![]() .
.
解得![]() .
.
因为C2的焦点![]() 在直线
在直线![]() 上,所以
上,所以![]() .
.
即![]() .
.
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ;
;
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() .
.
解法二 当C2的焦点在AB时,由(Ⅰ)知直线AB的斜率存在,设直线AB的方程
为![]() .
.
由 消去y得
消去y得![]() .
……①
.
……①
因为C2的焦点![]() 在直线
在直线![]() 上,
上,
所以![]() ,即
,即![]() .代入①有
.代入①有![]() .
.
即![]() .
……②
.
……②
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程②的两根,x1+x2=![]() .
.
由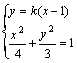 消去y得
消去y得![]() .
……③
.
……③
由于x1,x2也是方程③的两根,所以x1+x2=![]() .
.
从而![]() =
=![]() . 解得
. 解得![]() .
.
因为C2的焦点![]() 在直线
在直线![]() 上,所以
上,所以![]() .
.
即![]() .
.
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ;
;
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() .
.
解法三 设A、B的坐标分别为(x1,y1), (x2,y2),
因为AB既过C1的右焦点![]() ,又是过C2的焦点
,又是过C2的焦点![]() ,
,
所以![]() .
.
即![]() .
……①
.
……①
由(Ⅰ)知![]() ,于是直线AB的斜率
,于是直线AB的斜率 , ……②
, ……②
且直线AB的方程是![]() ,
,
所以![]() .
……③
.
……③
又因为![]() ,所以
,所以![]() .
……④
.
……④
将①、②、③代入④得![]() ,即
,即![]() .
.
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() ;
;
当![]() 时,直线AB的方程为
时,直线AB的方程为![]() .
.
