08届高考数学下学期阶段性检测理科试题
第Ⅰ卷(选择题 共50分)
一.选择题(本题共有10个小题,每小题5分,共50分;在每小题给出的四个选项中,只有一项是正确的,把正确的代号填在机读卡的指定位置上 )
1.若![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.
![]()
2.已知![]() 为两不相等的实数,集合
为两不相等的实数,集合![]() ,映射
,映射![]() 表示把
表示把![]() 中的元素
中的元素![]() 映射到集合
映射到集合![]() 中仍为
中仍为![]() ,则
,则![]() 等于( )
等于( )
A.1 B.2 C.3 D.4
3.已知方程![]() 的4个实根经过调整后组成一个以2为首项的等比数列,则
的4个实根经过调整后组成一个以2为首项的等比数列,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.24
D.24
4.从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若已知![]() , 求
, 求![]() 的值, 那么在以下四个答案:
①
的值, 那么在以下四个答案:
① ![]() ; ②
; ② ![]() ;
;
③ ![]() ; ④
; ④ ![]() 中, 正确的是( )
中, 正确的是( )
(A) ①和② (B) ②和③ (C) ③和④ (D) ①和④
6.椭圆![]() 的左准线为
的左准线为![]() ,左右焦点分别为
,左右焦点分别为![]() 和
和![]() ;抛物线
;抛物线![]() 的准线为
的准线为![]() ,焦点为
,焦点为![]() 与
与![]() 的一个交点为
的一个交点为![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() 平面上的一定点,
平面上的一定点,![]() 、
、![]() 、
、![]() 是平面上不共线的三个动点,点
是平面上不共线的三个动点,点![]() 满足
满足![]()
![]() ,则动点
,则动点![]() 的轨迹一定通过
的轨迹一定通过![]() 的( )
的( )
A.重心 B.垂心 C.外心 D.内心
8.![]() 是
是![]() 的导函数,
的导函数,![]() 的图象如图所示,则
的图象如图所示,则![]() 的
的
图象只可能是下图中的( )
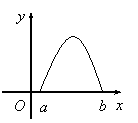
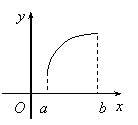
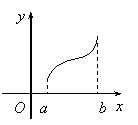
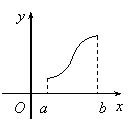
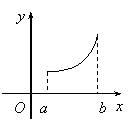
A. B. C. D.
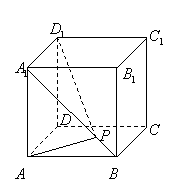 9.如右图所示,在单位正方体
9.如右图所示,在单位正方体![]() 的面对角线
的面对角线![]()
上存在一点![]() 使得
使得![]() 最短,则
最短,则![]() 的最小值为 ( )
的最小值为 ( )
A.2
B.![]()
C.![]() D.
D. ![]()
10.设三棱柱ABC—A1B1C1的所有棱长都为1米,有一个小虫从
点A开始按以下规则前进:在每一个顶点处等可能的选择通过
这个顶点的三条棱之一,并且沿着这条棱爬到尽头,则它爬了4米之后恰好位于顶点A的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.![]() 是虚数单位,复数
是虚数单位,复数![]() 的虚部为
.
的虚部为
.
12、对于正整数![]() 和
和![]() ,定义
,定义![]() !=
!=![]() ,其中
,其中![]() ,且
,且![]() 是满足
是满足![]() 的最大整数,则(
的最大整数,则(![]() !)/(10
!)/(10![]() !)=___________
!)=___________
13.由约束条件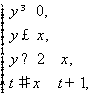 所确定的区域面积为
所确定的区域面积为![]() ,记
,记![]() ,则
,则![]() 等于
.
等于
.
14.函数![]() 图像上至少存在不同的三点到原点的距离构成等比数列,则公比的取值范围是_________________________.
图像上至少存在不同的三点到原点的距离构成等比数列,则公比的取值范围是_________________________.
15.对于集合![]() {1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对
{1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对![]() 、
、![]() 的情况,计算它的“交替和”的总和
的情况,计算它的“交替和”的总和![]() 、
、![]() ,并根据其结果猜测集合
,并根据其结果猜测集合![]() {1, 2, 3,…, n}的每一个非空子集的“交替和”的总和
{1, 2, 3,…, n}的每一个非空子集的“交替和”的总和![]() 。(不必给出证明)
。(不必给出证明)
三、解答题:本大题共6个小题.共75分.解答要写出文字说明、证明过程或解题步骤.
16.(本小题满分12分)已知![]() 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C![]() ,其中
,其中![]() .
.
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
17.(本小题满分12分)设a>0,函数f(x)=x3-ax在[1,+∞![]() 上是单调函数.
上是单调函数.
(1)求实数a的取值范围;
(2)设x0≥1,f(x0)≥1,且f(f(x0))=x0,求证:f(x0)=x0.
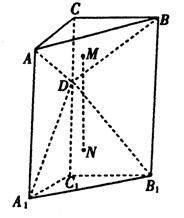
18.(本小题满分12分)
如图,直三棱柱ABC—A1B1C1中,![]() ,D为棱
,D为棱![]() 上的一动点,
上的一动点,![]() 、
、![]() 分别为
分别为![]() 的重心.
的重心.
(1)求证:![]() ;
;
(2)若二面角C—AB—D的大小为![]() ,求点C1到平面A1B1D的距离;
,求点C1到平面A1B1D的距离;
(3)若点C在![]() 上的射影正好为M,试判断点C1在
上的射影正好为M,试判断点C1在![]() 的射影是否
的射影是否
为N?并说明理由.
19.(本小题满分12分)
已知某车站每天8:00—9:00、9:00—10:00都恰好有一辆客车到站;8:00—9:00到站的客车![]() 可能在8:10、8:30、8:50到,其概率依次为
可能在8:10、8:30、8:50到,其概率依次为![]() .9:00—10:00到站的客车
.9:00—10:00到站的客车![]() 可能在9:10、9:30、9:50到,其概率依次为
可能在9:10、9:30、9:50到,其概率依次为![]() .今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
.今有甲、乙两位旅客,他们到站的时间分别为8:00和8:20,试问他们候车时间的平均值哪个更多?
20. (本小题满分13分)
已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。 设数列
成立。 设数列![]() 的前
的前![]() 项和
项和![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)试构造一个数列![]() ,(写出
,(写出![]() 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数![]() 都有
都有![]() ,且
,且![]() ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数。令
的变号数。令![]() (
(![]() 为正整数),求数列
为正整数),求数列![]() 的变号数。
的变号数。
21.(本小题满分14分)
如图,棱长为1的正方体, ![]() 、
、![]() 为
为![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 的中点,过
的中点,过![]() 作直线与
作直线与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]() ,
,
(1)
求![]() 的长度;
的长度;
(2)
将平面![]() 无限延展开来,设平面
无限延展开来,设平面![]() 内有一动点
内有一动点![]() ,它到直线
,它到直线![]() 的距离减去它到
的距离减去它到![]() 点的距离的平方差为1,请建立适当的直角坐标系,
点的距离的平方差为1,请建立适当的直角坐标系,
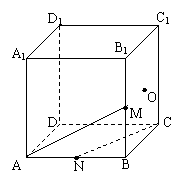 求出动点
求出动点![]() 所构成曲线
所构成曲线![]() 的方程;
的方程;
(3)
在(2)的条件下,请说明以![]() 为直径的圆与曲线
为直径的圆与曲线
![]() 是否有交点,如果有请求出;如果没有请使
是否有交点,如果有请求出;如果没有请使
用适当的文字加以说明
参考答案
一、选择题 C D D A B B C D C B
二、填空题 11. ![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ; 14.
; 14. ![]() ; 15.
; 15. ![]()
三、解答题
16.解:(1)∵![]() 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C![]() ,
,
∴![]() ,
,![]()
由![]() 得,
得,![]()
即 ![]()
∵ ![]() , ∴
, ∴ ![]() .
.
(2)由![]() 得,
得,![]()
即 ![]() ,
,
∴ ![]() ,
,![]()
又 ![]() , ∴
, ∴![]() ,
,![]()
![]()
∴ ![]() .
.
17.解(1)y′=f ′(x)=3x2-a.
若f(x)在[1,+∞]上是单调递减函数,则须y′<0,即a>3x2,这样的实数a不存在,
故f(x)在[1,+∞]上不可能是单调递减函数.
若f(x)在[1,+∞]上是单调递增函数,则a≤3x2,由于x∈[1,+∞],故3x2≥3.从而0<a≤3 .
(6分)
(2)方法一 (反证法)由(1)可知f(x)在[1,+∞)上只能为单调递增函数.假设f(x0)≠x0,
若1≤x0<f(x0),则f(x0)<f(f(x0))=x0矛盾,
若1≤f(x0)<x0,则f(f(x0))<f(x0),即x0<f(x0)矛盾,
故只有f(x0)=x0成立. (12分)
方法二
设f(x0)=u,则f(u)=x0,∴x![]() -ax0=u,u3-au=x0,两式相减得(x
-ax0=u,u3-au=x0,两式相减得(x![]() -u3)-a(x0-u)=u-x0,
-u3)-a(x0-u)=u-x0,
∴(x0-u)(x![]() +x0u+u2+1-a)=0,∵x0≥1,u≥1,∴x
+x0u+u2+1-a)=0,∵x0≥1,u≥1,∴x![]() +x0u+u2≥3.
+x0u+u2≥3.
又0<a≤3,∴x![]() +x0u+u2+1-a>0.
+x0u+u2+1-a>0.
∴x0-u=0,即u=x0,亦即f(x0)=x0.
(18)解:(1)连结![]() 并延长,分别交
并延长,分别交![]() 于
于![]() ,连结
,连结![]() ,
,
![]() 分别为
分别为![]() 的重心,则
的重心,则![]() 分别为
分别为![]() 的中点
的中点![]()
![]() 在直三棱柱
在直三棱柱![]() 中,
中,![]()
(2)连结![]()
![]() 即为二面角
即为二面角![]() 的平面角
的平面角![]()
在![]() 中,
中,![]()
![]()
![]()
连结![]()
同上可知,![]()
设![]()
![]()
![]()
![]()
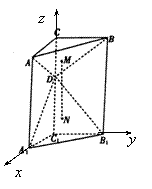 (3)
(3)![]()
![]()
![]()
![]()
![]() ∽
∽![]()
![]()
![]()
![]() .
.
解法二:空间向量解法:以C1为原点,如图建立空间直角坐标系。
(1) 设![]() ,依题意有:
,依题意有:
![]()
因为M、N分别为![]() 的重心.
的重心.
所以![]()
∵![]() ∴
∴![]()
(2)
因为平面ABC的法向量![]() , 设平面ABD的法 向量
, 设平面ABD的法 向量![]()
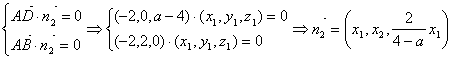
令![]() ,设二面角C—AB—D为
,设二面角C—AB—D为![]() ,则由
,则由![]()
因此 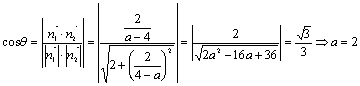
设平面A1B1D的法向量为![]() ,则
,则
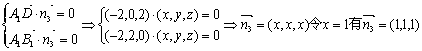
设C1到平面A1B1D的距离为![]() ,则
,则![]()
(3)若点C在平面ABD上的射影正好为M,则![]()
|
因为D为CC1的中点,根据对称性可知C1在平面A1B1D的射影正好为N。
19.本题考查离散型随机变量的分布列,考查运用数学知识解决问题的能力,以及推理和运算能力
|
| 10 | 30 | 50 | 70 | 90 |
|
|
|
|
|
|
|
旅客甲候车时间的平均值比乙多.设甲、乙两位旅客的候车时间分别为![]() 分钟,则他们的分布列为:
分钟,则他们的分布列为:
甲旅客 乙旅客
|
| 10 | 30 | 50 |
|
|
|
|
|
易知![]() ,
,
![]() ,
,![]() ,旅客甲候车时间的平均值比乙多.
,旅客甲候车时间的平均值比乙多.
20.解:(1)∵![]() 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴![]() ,
,
当![]() 时,函数
时,函数![]() 在
在![]() 上递增,故不存在
上递增,故不存在![]() ,使得不等式
,使得不等式![]() 成立。
成立。
当![]() 时,函数
时,函数![]() 在
在![]() 上递减,故存在
上递减,故存在![]() ,使得不等式
,使得不等式![]() 成立。
成立。
综上,得![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
(2)要使![]() ,可构造数列
,可构造数列![]() ,∵对任意的正整数
,∵对任意的正整数![]() 都有
都有![]() ,
,
∴当![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立,即
恒成立,即![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,等等。
,等等。
(3)解法一:由题设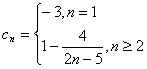 ,
,
∵![]() 时,
时,![]() ,∴
,∴![]() 时,数列
时,数列![]() 递增,
递增,
∵![]() ,由
,由![]() ,可知
,可知![]() ,即
,即![]() 时,有且只有
时,有且只有![]() 个变号数;
个变号数;
又∵![]() ,即
,即![]() ,∴此处变号数有
,∴此处变号数有![]() 个。
个。
综上得 数列![]() 共有
共有![]() 个变号数,即变号数为
个变号数,即变号数为![]() 。
。
解法二:由题设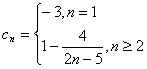 ,
,
![]() 时,令
时,令![]() ;
;
又∵![]() ,∴
,∴![]() 时也有
时也有![]() 。
。
综上得 数列![]() 共有
共有![]() 个变号数,即变号数为
个变号数,即变号数为![]() 。
。
21. 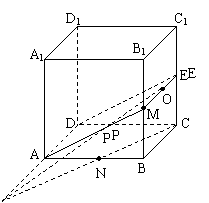 (1)如图,连
(1)如图,连![]() 交
交![]() 于
于![]() ,连
,连![]() ,延长
,延长![]() ,
, ![]() 交于
交于![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,则
,则![]() 为所求的线段,易得
为所求的线段,易得![]() ,
,
在![]() 中,可得到
中,可得到
![]() ,
,
|
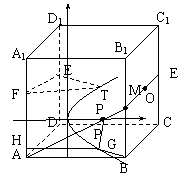 (2)过
(2)过![]() 作
作![]() ,过
,过![]() 作
作![]() ,
,
又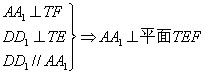 ,故
,故![]() .
.
在![]() 中,
中,
![]()
故![]() 点的轨迹是以
点的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,
为准线的抛物线,
以过![]() 点且垂直于
点且垂直于![]() 的直线为
的直线为![]() 轴,以
轴,以![]() 点
点![]() 的垂线段的中点为原点,建立直角坐标系,设抛物线的方程
的垂线段的中点为原点,建立直角坐标系,设抛物线的方程![]() ,由于
,由于![]() 点到
点到![]() 的距离为
的距离为![]() ,故
,故![]() ,
,
∴曲线K的方程为![]()
(3)假设抛物线与圆有交点,设交点为![]() ,则
,则![]() 为直角,易得
为直角,易得![]()
故![]() ,又
,又![]() ,过
,过![]() 作
作![]() 则
则![]()
![]() ,与
,与![]() 矛盾,故交点
矛盾,故交点![]() 不存在,于是以
不存在,于是以![]() 为直径的圆与曲线
为直径的圆与曲线![]() 是没有交点.
是没有交点.