08届高考数学基础调研测试试题
一、.填空题(共14小题,每题5分,计70分)
1.已知![]() 为实数集,
为实数集,![]() ,则
,则![]() ▲ .
▲ .
2.设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线![]() 与
与![]() 的位置关系是
▲
.
的位置关系是
▲
.
3.若复数![]() (其中,
(其中,![]() 为虚数单位),则
为虚数单位),则![]() ▲ .
▲ .
4.已知过点A(-2,m)和B(m,4)的直线与直线2x+y+1=0平行,则m的值为 ▲ .
5.已知实数![]() 满足
满足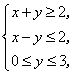 则
则![]() 的取值范围是 ▲ .
的取值范围是 ▲ .
6.如果数据x1、x2、…、xn 的平均值为![]() ,方差为S2 ,则3x1+5、3x2+5、…、3xn+5 的方差为
▲
.
,方差为S2 ,则3x1+5、3x2+5、…、3xn+5 的方差为
▲
.
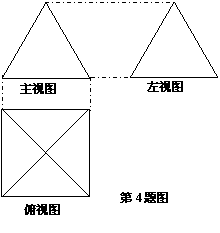
7.如图(下面),一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则其体积是 ▲
8.椭圆![]() 上任意一点到两焦点的距离分别为
上任意一点到两焦点的距离分别为![]() 、
、![]() ,焦距为
,焦距为![]() ,若
,若![]() 、
、![]() 、
、![]() 成等差数列,则椭圆的离心率为 ▲ .
成等差数列,则椭圆的离心率为 ▲ .
9.设a,b为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若a∥b,lÌa,则l∥b; ②若mÌa,nÌa,m∥b,n∥b,则a∥b; ③若l∥a,l⊥b,则a⊥b; ④若m、n是异面直线,m∥a,n∥a,且l⊥m,l⊥n,则l⊥a.
其中真命题的序号是 ▲ .
10.函数![]() 的图象恒过定点
的图象恒过定点![]() ,若点
,若点![]() 在直线
在直线![]() 上,其中
上,其中![]() ,则
,则![]() 的最小值为 ▲ .
的最小值为 ▲ .
11.已知![]() ,则
,则![]() ▲ .
▲ .
12.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数![]() (
(![]() =1,2,3,…,12)来表示,已知6月份的月平均气
=1,2,3,…,12)来表示,已知6月份的月平均气
温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为 ▲ ℃.
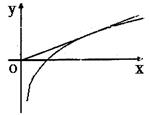
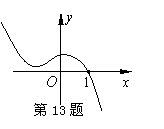 13.已知函数y=f(x)的图象如图,则不等式f()>0的解集为 ▲_ .
13.已知函数y=f(x)的图象如图,则不等式f()>0的解集为 ▲_ .
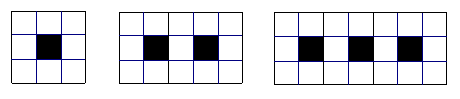
14.用黑白两种颜色的正方形地砖依照下图的规律
拼成若干图形,则按此规律第100个图形中有白色
地砖 ▲_ 块;现将一粒豆子随机撒在第100个图
中,则豆子落在白色地砖上的概率是 ▲_ .
|
第1个 第2个 第3个
二、解答题(6大题共90分,要求有必要的文字说明和步骤)
15.(本题满分14分)已知△ABC的面积S满足3≤S≤3![]() 且
且![]() 的夹角为
的夹角为![]() ,
,
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)求![]() 的最小值。
的最小值。
16. (本题满分14分)如图,
(本题满分14分)如图,![]() 为空间四点
为空间四点![]() 在
在![]() 中,
中,![]()
![]() 等边三角形
等边三角形![]() 以
以![]() 为轴运动
为轴运动![]()
(Ⅰ)当平面![]() 平面
平面![]() 时,求
时,求![]() ;
;
(Ⅱ)当![]() 转动时,是否总有
转动时,是否总有![]() ?证明你的结论
?证明你的结论![]()
17.(本题满分15分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(量大供应量)如下表所示:
|
消耗量 资源 | 甲产品(每吨) | 乙产品(每吨) | 资源限额(每天) |
| 煤(t) | 9 | 4 | 360 |
| 电力(kw·h) | 4 | 5 | 200 |
| 劳动力(个) | 3 | 10 | 300 |
| 利润(万元) | 6 | 12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
18.(本题满分15分)在公差为d(d≠0)的等差数列{an}和公比为q的等比数列{bn}中,已知a1=b1=1,a2=b2,a8=b3.
(1)求数列{an}与{bn}的通项公式;
(2)令![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
19.(本小题满分16分)
已知椭圆![]() 的离心率为
的离心率为![]() ,直线
,直线![]() :
:![]() 与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点F2,直线![]() 过点F1且垂直于椭圆的长轴,动直线
过点F1且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点P,线段PF2垂直平分线交
于点P,线段PF2垂直平分线交![]() 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足![]() ,求
,求![]() 的取值范围。
的取值范围。
20.(本小题满分16分)
定义域为R的偶函数![]() ,方程
,方程![]() 在R上恰有5个不同的实数解.
在R上恰有5个不同的实数解.
(Ⅰ)求x<0时,函数![]() 的解析式;
的解析式;
(Ⅱ)求实数a的取值范围.
答案
1.![]() ; 2.垂直; 3.
; 2.垂直; 3.![]() ; 4.
; 4.![]() ; 5.
; 5.![]() ;
;
6.9S2; 7.![]() ; 8.
; 8.![]() ; 9.①③④; 10.8;
; 9.①③④; 10.8;
11.7/8; 12.20.5; 13.(-2,1); 14.503 503/603 。
15.(Ⅰ)由题意知![]()
![]()
![]()
![]()
![]()
![]() 的夹角
的夹角
![]()
![]()
(Ⅱ)![]()
![]()
![]()
![]()
![]() 有最小值。
有最小值。
![]() 的最小值是
的最小值是![]()
16.解: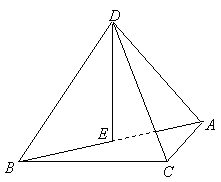 (Ⅰ)取
(Ⅰ)取![]() 的中点
的中点![]() ,连结
,连结![]() ,因为
,因为![]() 是等边三角形,所以
是等边三角形,所以![]()
![]()
当平面![]() 平面
平面![]() 时,
时,
因为平面![]() 平面
平面![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
可知![]()
![]()
由已知可得![]() ,在
,在![]() 中,
中,![]()
![]()
(Ⅱ)当![]() 以
以![]() 为轴转动时,总有
为轴转动时,总有![]()
![]()
证明:
(ⅰ)当![]() 在平面
在平面![]() 内时,因为
内时,因为![]() ,所以
,所以![]() 都在线段
都在线段![]() 的垂直平分线上,即
的垂直平分线上,即![]()
![]()
(ⅱ)当![]() 不在平面
不在平面![]() 内时,由(Ⅰ)知
内时,由(Ⅰ)知![]()
![]() 又因
又因![]() ,所以
,所以![]()
![]()
又![]() 为相交直线,所以
为相交直线,所以![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,得
,得![]()
![]()
综上所述,总有![]()
![]()
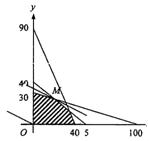
17.解:设此工厂应分别生产甲、乙两种产品x吨、y吨. 获得利润z万元
|
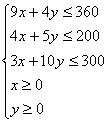
作出可行域如右图
利润目标函数z=6x+12y
由几何意义知当直线l:z=6x+12y,经过可行域上的点M时,z=6x+12y取最大值.
解方程组 ![]() ,得M(20,24)
,得M(20,24)
答:生产甲种产品20t,乙种产品24t,才能使此工厂获得最大利润
18.解:(1)由条件得: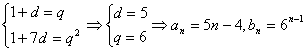
(2)![]() ①
①
∴6Tn=6+6×62+11×63+…+(5n-4)6n ②
①-②:![]()
![]()
∴![]()
19.解:(1)![]() ,
,![]()
∵直线l:x-y+2=0与圆x2+y2=b2相切,∴![]() =b,∴b=
=b,∴b=![]() ,b2=2,∴
,b2=2,∴![]() =3. ∴椭圆C1的方程是
=3. ∴椭圆C1的方程是![]()
(2)∵MP=MF,∴动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离,
∴动点M的轨迹是以l1为准线,F2为焦点的抛物线,∴点M的轨迹C2的方程为![]() 。(3)Q(0,0),设
。(3)Q(0,0),设![]() ,
,
![]() ,
,
由![]() 得
得 ![]() ,
,
![]() ,
,![]() 化简得
化简得![]() ,
,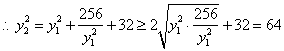
当且仅当![]() 时等号成立,
时等号成立,
![]() ,又∵y22≥64,
,又∵y22≥64,
∴当![]() . 故
. 故![]() 的取值范围是
的取值范围是![]() .
.
20.解:(1)设x<0,则-x>0
∵![]() 为偶函数, ∴
为偶函数, ∴![]()
(2)∵![]() 为偶函数,∴
为偶函数,∴![]() =0的根关于0对称.
=0的根关于0对称.
由![]() =0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.
=0恰有5个不同的实数解,知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
∴原命题![]() 图像与x轴恰有两个不同的交点
图像与x轴恰有两个不同的交点
下面研究x>0时的情况
∵![]()
即 ![]() 为单调增函数,故
为单调增函数,故![]() 不可能有两实根
不可能有两实根
∴a>0 令![]()
当![]() 递减,
递减,
∴![]() 处取到极大值
处取到极大值![]()
又当![]()
要使![]() 轴有两个交点当且仅当
轴有两个交点当且仅当![]() >0
>0
解得![]() ,故实数a的取值范围(0,
,故实数a的取值范围(0,![]() )
)
方法二:
(2)∵![]() 为偶函数, ∴
为偶函数, ∴![]() =0的根关于0对称.
=0的根关于0对称.
由![]() =0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
=0恰有5个不同的实数解知5个实根中有两个正根,二个负根,一个零根.
且两个正根和二个负根互为相反数
∴原命题![]() 图像与x轴恰有两个不同的交点
图像与x轴恰有两个不同的交点
下面研究x>0时的情况
![]() 与直线
与直线![]() 交点的个数.
交点的个数.
∴当![]() 时,
时,![]() 递增与直线y=ax下降或是x国,
递增与直线y=ax下降或是x国,
故交点的个数为1,不合题意 ∴a>0
|
设切点![]()
∴切线方为 ![]()
由切线与y=ax重合知![]()
故实数a的取值范围为(0,![]() )
)
 产品
产品