函数综合训练(一)
一. 教学内容:
函数综合训练(一)
【模拟试题】(答题时间:120分钟)
一. 选择题(每小题5分,共50分)
1. 函数![]() 的定义域为A,函数
的定义域为A,函数![]() 的定义域为B,若
的定义域为B,若![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 函数![]() 在区间
在区间![]() 上递减,则实数
上递减,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 已知![]() ,且
,且![]() ,则
,则![]() 满足( )
满足( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 定义在R上的奇函数![]() 为减函数,设
为减函数,设![]() ,给出下列不等式:
,给出下列不等式:
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
其中正确的不等式序号是( )
A. (1)(2)(4) B. (1)(4) C. (2)(4) D. (1)(3)
5. 偶函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 与
与![]() 的大小关系为( )
的大小关系为( )
A. ![]() B.
B.
![]()
C. ![]() D.
不能确定
D.
不能确定
6. 已知定义域为R的函数![]() 满足
满足![]() ,有
,有![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() ( )
( )
A. 2 B. 4 C. ![]() D.
D. ![]()
7. 已知定义在R上的偶函数![]() 在区间
在区间![]() 上为增函数,且
上为增函数,且![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 已知函数![]() 是R上的偶函数,且满足:
是R上的偶函数,且满足:![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ( )
( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
9. 函数![]() 是
是![]() 上的增函数,函数
上的增函数,函数![]() 是偶函数,则下列结论中正确的是( )
是偶函数,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
10. 设![]() 、
、![]() 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当![]() 时,
时,![]() ,且
,且![]() ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
二. 填空题(每小题4分,共24分)
11. 定义在R上的函数![]() 满足
满足![]() ,则
,则![]()
![]()
![]() 。
。
12. 已知函数 ,则
,则![]() 。
。
13. 设![]() ,
,![]() ,且
,且![]() ,那么函数
,那么函数![]() 的最大值是 。
的最大值是 。
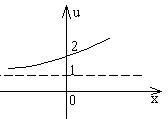
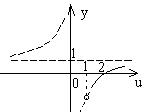
14. 已知![]() 为偶函数,
为偶函数,![]() 为奇函数,它们的定义域都为
为奇函数,它们的定义域都为![]() ,当
,当![]() 时,它们的图象如下图,则不等式
时,它们的图象如下图,则不等式![]() 的解集为
。
的解集为
。
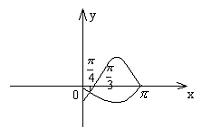
15. 已知二次函数![]() ,若在区间
,若在区间![]() 内至少存在一个实数
内至少存在一个实数![]() ,使
,使![]() ,则实数
,则实数![]() 的取值范围是
。
的取值范围是
。
16. 设函数![]() ,给出下列命题
,给出下列命题
(1)![]() 时,
时,![]() 为奇函数;
为奇函数;
(2)![]() ,
,![]() 时,方程
时,方程![]() 只有一个实数根;
只有一个实数根;
(3)![]() 的图象关于点
的图象关于点![]() 对称;
对称;
(4)方程![]() 至多有两个实数根。
至多有两个实数根。
上述四个命题中所有正确的命题序号为 。
三. 解答题(共76分)
17. 已知集合![]() ,集合
,集合![]()
![]() ,其中
,其中![]() ,设全集
,设全集![]() ,
,![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
18. 求函数![]() 的值域(满分12分)
的值域(满分12分)
19. 已知两个函数![]()
(1)若![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(2)若![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围。(满分12分)
的取值范围。(满分12分)
20. 已知奇函数![]()
![]() 。
。
(1)确定![]() 的值,并证明
的值,并证明![]() 在R上为增函数;
在R上为增函数;
(2)若方程![]() 在
在![]() 上有解,证明
上有解,证明![]() 。(满分12分)
。(满分12分)
21. 已知函数![]() 满足
满足![]() ,其中
,其中![]() ,且
,且![]() 。
。
(1)对于函数![]() ,当
,当![]() 时,
时,![]() ,求实数m的取值范围;
,求实数m的取值范围;
(2)当![]() 时,
时,![]() 的取值范围恰为
的取值范围恰为![]() ,求
,求![]() 的取值范围。(满分14分)
的取值范围。(满分14分)
22. 已知函数![]() 。
。
(1)求函数![]() 的反函数
的反函数![]() 和
和![]() 的导函数
的导函数![]() ;
;
(2)假设对![]() ,不等式
,不等式![]() 成立,求实数
成立,求实数![]() 的取值范围。(满分14分)
的取值范围。(满分14分)
【试题答案】
一.
1. A 2. D 3. B 4. B 5. C 6. B 7. C 8. A 9. B 10. D
二.
11. 7 12. ![]() 13. 0 14.
13. 0 14. ![]() 15.
15. ![]() 16.(1)(2)(3)
16.(1)(2)(3)
三.
17.
解:![]()
![]() ∴
∴ ![]()
![]() ,
,![]()
![]()
设![]() ,则
,则![]() ∴
∴ ![]() ,
,![]()
若![]() ,则
,则![]()
![]()
∴ ![]() ∴
∴ ![]() ∴
∴ 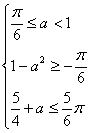 ∴
∴ ![]()
若![]() ,则
,则![]() 在
在![]() 上
上![]()
∴ ![]()
![]() ∴
∴ ![]()
∵ ![]() ∴
∴ 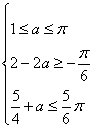 ∴
∴ ![]()
综上所述:![]()
18.
解:![]() 定义域:R
定义域:R
设![]() ,则
,则![]() ,且
,且![]()
∴ ![]() (
(![]() )
)
∵ 函数![]() 在
在![]() 上
上![]()
∴ 当![]() 时,
时,![]()
![]()
∴ 函数![]() 的值域为
的值域为![]()
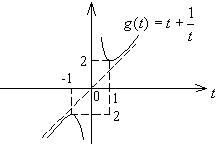
19.
解:∵ ![]()
∴ ![]()
令![]() ,得
,得![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
0 -
0
+
+
0 -
0
+
![]()
![]()
![]() 极大值
极大值![]()
![]() 极小值
极小值 ![]()
![]() 111
111
![]() 在
在![]() 上
上![]() ,在
,在![]() 上
上![]()
(1)∵![]() 都有
都有![]() 成立
成立
∴ 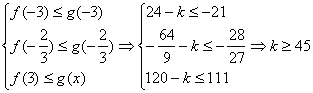
(2)∵![]() 都有
都有![]() 成立
成立
∴ ![]() ,即
,即![]() ∴
∴ ![]()
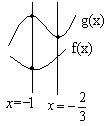
20.
解:(1)∵ ![]() 为R上的奇函数
为R上的奇函数
∴ ![]() ∴
∴ ![]() ∴
∴ ![]()
设![]()
![]() ,
,![]()
∵ ![]() 在R上
在R上![]() ,且
,且![]()
![]() 在
在![]() 上
上![]()
∴ ![]() 在R上
在R上![]()
(2)∵ ![]() 在R上
在R上![]() ,且当
,且当![]() 时有
时有![]() ,
,![]()
∴ 当![]() 时,
时,![]() 的值域为
的值域为![]()
∵ 方程![]() 在
在![]() 上有解
∴
上有解
∴ ![]()
∴ ![]() 即
即![]()
21.
解: ![]() 且
且![]()
设![]() ,则
,则![]() ∴
∴ ![]()
∴ ![]()
当![]() 时,∵
时,∵ ![]()
![]()
![]()
![]()
![]() ∴
∴ ![]() 在其定义域上
在其定义域上![]()
当![]() 时,∵
时,∵ ![]() ,
,![]()
![]() ,
,![]()
![]() ∴
∴ ![]() 在其定义域上
在其定义域上![]()
∴ ![]() 且
且![]() ,都有
,都有![]() 为其定义域上的增函数
为其定义域上的增函数
又∵ ![]() ∴
∴ ![]() 为奇函数
为奇函数
(1)∵ 当![]() 时,
时,![]()
∴ ![]()
∴ 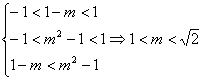
(2)当![]() 时,∵
时,∵ ![]() 在
在![]() 上
上![]() ,且值域为
,且值域为![]()
∴ ![]()
![]()
![]()
![]() ∴
∴ ![]()
22.
解:(1)![]()
![]()
![]()
![]()
∴ ![]() ∵
∵ ![]() ∴
∴ ![]()
(2)∵ ![]() ,
,![]() 成立
成立
∴ ![]()
∴ ![]()
设![]() ,
,![]()
![]()
∴ ![]() 恒有
恒有![]() 成立
成立
![]() ∵
∵ ![]() ∴
∴ ![]()
∴ ![]() ∴
∴ ![]() ,
,![]()
∴ ![]() ,
,![]() 在
在![]() 上
上![]()
∴ ![]()
即![]()
![]()
∵ ![]() ∴
∴ ![]() 在
在![]() 上
上![]()
∴ ![]()
![]()
![]()
∴ ![]() 的取值范围是
的取值范围是![]()
