高考理科数学复习第一阶段质量检测
数学试题() 2008.03
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上;
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净,再选涂其它答案.不能答在试卷上。
3.考试结束,将第Ⅱ卷和答题卡一并交回。
一、选择题(本大题共12个小题;每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.)
1.设U为全集,M、P是U的两个子集,且![]() ,则
,则![]() ( )
( )
A.
M B. P C. ![]() D.
D.
![]()
2.![]() 是虚数单位,则复数
是虚数单位,则复数![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
3. 要完成下列两项调查:①从某社区125户高收入家庭、280户中等收入家庭、95户低收入人家庭中选出100户调查社会购买力的某项指标;②某中学的15名艺术特长生中选出3人调查学习负担情况。宜采用的抽样方法依次为( )
A.①随机抽样法,②系统抽样法 B.①分层抽样法,②随机抽样法
C.①系统抽样法,②分层抽样法 D.①②都用分层抽样法
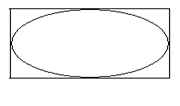 4.如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为70颗,以此实验数据为依据可以估计出椭圆的面积大约为( ).
4.如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为70颗,以此实验数据为依据可以估计出椭圆的面积大约为( ).
A.6 B.12
C.18 D.20
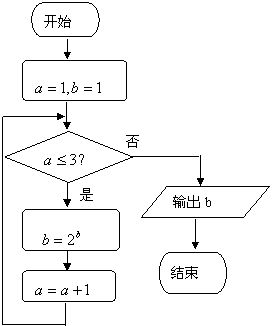
5.如图,该程序运行后输出的结果为 ( )
A.1 B.2
C.4 D.16
6.设![]() 、
、![]() 满足条件
满足条件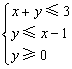 ,则
,则![]() 的最小值等于( )
的最小值等于( )
A.4 B. 5 C.6 D.7
7.函数![]() 的图象与函数
的图象与函数![]() 的图象关于( )
的图象关于( )
A.点![]() 对称 B.直线
对称 B.直线![]() 对称 C.点
对称 C.点![]() 对称 D.直线
对称 D.直线![]() 对称
对称
8. 我国于07年10月24日成功发射嫦娥一号卫星,并经四次变轨飞向月球。嫦娥一号绕地球运行的轨迹是以地球的地心为焦点的椭圆。若第一次变轨前卫星的近地点到地心的距离为m,远地点到地心的距离为n,第二次变轨后两距离分别为2m、2n(近地点是指卫星距离地面最近的点,远地点是距离地面最远的点),则第一次变轨前的椭圆的离心率比第二次变轨后的椭圆的离心率( )
A.不变 B. 变小 C. 变大 D.无法确定
9.设函数![]() 的最大值为3,则f(x)的图象的一条对称轴的方程是( )
的最大值为3,则f(x)的图象的一条对称轴的方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
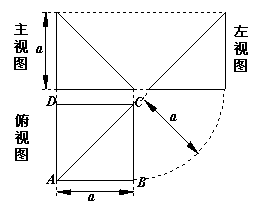
10.四棱锥![]() 的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
的顶点P在底面ABCD中的投影恰好是A,其三视图如图:
则四棱锥![]() 的表面积为( )
的表面积为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D. ![]()
11. 给出下列四个命题,其中真命题为( )
①命题“![]() x∈R,使得x2+1>3x”的否定是“
x∈R,使得x2+1>3x”的否定是“![]() x∈R,都有x2+1≤3x”;
x∈R,都有x2+1≤3x”;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆![]() 与坐标轴有
与坐标轴有![]() 个交点分别为
个交点分别为![]() 则
则![]() ;
;
④函数![]() 的零点个数有3个.
的零点个数有3个.
A. ①④ B.②④ C. ①③ D. ② ③
12.已知O是△ABC所在平面上一定点,动点P满足
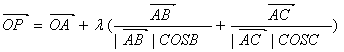 ,
,![]() ,则动点P的轨迹一定通过△ABC的( )
,则动点P的轨迹一定通过△ABC的( )
A.内心 B.垂心 C.外心 D.重心
济宁市2007—2008学年度高三复习第一阶段质量检测
数学试题(理科) 2008.03
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4个小题;每小题4分,共16分)
13.抛物线![]() 的焦点恰好为双曲线
的焦点恰好为双曲线![]() 的上焦点,则
的上焦点,则![]() .
.
14.设![]() =
=![]() ,则二项式
,则二项式![]() 展开式中含
展开式中含![]() 项的系数是 .
项的系数是 .
15. 在计算机的算法语言中有一种函数![]() 叫做取整函数(也称高斯函数),它表示
叫做取整函数(也称高斯函数),它表示![]() 的整数部分,即[
的整数部分,即[![]() ]是不超过
]是不超过![]() 的最大整数.例如:
的最大整数.例如:![]() .设函数
.设函数![]() ,则函数
,则函数![]() 的值域为 _______________.
的值域为 _______________.
16.设等边![]() 的边长为
的边长为![]() ,
,![]() 是
是![]() 内任意一点,且
内任意一点,且![]() 到三边
到三边![]() 、
、![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() 、
、![]() ,则有
,则有![]() 为定值
为定值![]() ;由以上平面图形的特性类比到空间图形:设正四面体
;由以上平面图形的特性类比到空间图形:设正四面体![]() 的棱长为
的棱长为![]() ,
,![]() 是正四面体
是正四面体![]() 内任意一点,且
内任意一点,且![]() 到平面
到平面![]() 、平面
、平面![]() 、平面
、平面![]() 、平面
、平面![]() 的距离分别为
的距离分别为![]() 、
、![]() 、
、![]() ,则有
,则有![]() 为定值 .
为定值 .
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)
17.(本题满分12分) 在△ABC中,设A、B、C的对边分别为a、b、c,向量![]() =(cosA,sinA),
=(cosA,sinA),
![]() =(
=(![]() ),若
),若![]() =2.
=2.
(1)求角A的大小;
(2)若![]() 的面积.
的面积.
18. (本题满分12分) 在一次电视节目的抢答中,题型为判断题,只有“对”和“错”两种结果,其中某选手判断正确的概率为![]() ,判断错误的概率为
,判断错误的概率为![]() ,若判断正确则加1分,判断错误则减1分,现记“该选手答完
,若判断正确则加1分,判断错误则减1分,现记“该选手答完![]() 题后总得分为
题后总得分为![]() ”.
”.
(1)当![]() 时,记
时,记![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)当![]() 时,求
时,求![]() 且
且![]() 的概率.
的概率.
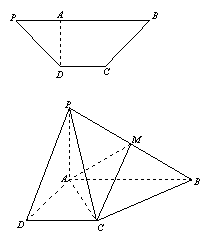 19.(本小题满分12分) 在等腰梯形
19.(本小题满分12分) 在等腰梯形![]() 中(如图1),
中(如图1),![]() ,
,![]() ,
,![]() ,
, ![]() 于点
于点![]() ;将
;将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() (如图2),点
(如图2),点![]() 在棱
在棱![]() 上,平面
上,平面![]() 把几何体
把几何体![]() 分成的两部分体积比
分成的两部分体积比![]()
(1)确定点M在![]() 上的位置;
上的位置;
(2)判断直线![]() 是否平行于平面
是否平行于平面![]() ,并说明理由;
,并说明理由;
(3)求二面角![]() 的正切值.
的正切值.
20.(本小题满分12分) 已知函数f(x)=x2-x+alnx, ![]()
(1)若![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)求![]() 的单调区间.
的单调区间.
21. (本小题满分12分) 已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() ,一个长轴端点为
,一个长轴端点为![]() ,短轴端点和焦点所组成的四边形为正方形,直线
,短轴端点和焦点所组成的四边形为正方形,直线![]() 与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且![]() .
.
(1)求椭圆方程;
(2)求m的取值范围.
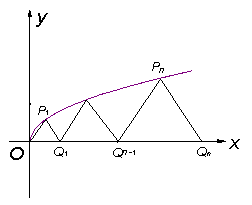
22. (本小题满分14分) 幂函数y = 的图象上的点 Pn(tn2,tn)(n = 1,2,……)与 x 轴正半轴上的点 Qn 及原点 O 构成一系列正△PnQn-1Qn(Q0与O重合),记 an = Qn-1Qn
(1)求 a1的值;
(2)求数列 {an} 的通项公式 an;
(3)设 Sn为数列 {an} 的前 n 项和,若对于任意的实数 l∈[0,1], 3Sn-3n + 2≥(1-l) (3an-1) 恒成立,求 n 的取值范围.
济宁市2007—2008学年度高三复习第一阶段质量检测
数学试题参考答案及评分标准(理)
一.选择题(每小题5分,共60分)
1.D 2.D 3.B 4.C 5.D 6.A 7.B 8.A 9.A 10.D 11.C 12.B
二.填空题(每小题4分,共16分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三.解答题
17. 解:(1)![]()
![]()
![]()
![]() ………………………2分
………………………2分
![]()
![]()
![]()
![]() …………………………4分
…………………………4分
又![]()
![]()
![]()
![]() …………………6分
…………………6分
另解:![]() …………………2分
…………………2分
![]()
![]() ………………………4分
………………………4分
![]()
![]()
![]() ……………………5分
……………………5分
![]()
![]() ………………………………6分
………………………………6分
(2)由余弦定理,
![]()
![]() ………………8分
………………8分
即![]()
![]() ……………………………………10分
……………………………………10分
![]() …………………………12分
…………………………12分
另解:由![]()
![]()
![]()
又![]() …………………………………10分
…………………………………10分
∴△ABC为等腰直角三角形。
![]() ……………………………………12分
……………………………………12分
18. 解:(1)![]() 的取值为1,3,又
的取值为1,3,又![]() ; ………………………2分
; ………………………2分
故![]() ,
,![]() .
.
所以 ξ的分布列为:
|
| 1 | 3 |
|
|
|
|
……………………………4分
且![]() =1×
=1×![]() +3×
+3×![]() =
=![]() ;………………………………………………6分
;………………………………………………6分
(2)当S8=2时,即答完8题后,回答正确的题数为5题,
回答错误的题数是3题, ……………………………………………8分
又已知![]() ,若第一题和第二题回答正确,则其余6题可任意答对3题;若第一题和第三题回答正确,第二题回答错误,
,若第一题和第二题回答正确,则其余6题可任意答对3题;若第一题和第三题回答正确,第二题回答错误,
则后5题可任意答对3题. ………………………………10分
此时的概率为![]() .…………………12分
.…………………12分
19. (Ⅰ)∵平面![]() 平面
平面![]() ,
,![]()
∴![]() 平面
平面![]()
∴平面![]() 平面
平面![]()
在平面![]() 内,由
内,由![]() 作
作![]() 于点
于点![]()
∴![]() 平面
平面![]() ……………………………2分
……………………………2分
∵![]()
∴![]() ,从而
,从而![]()
∴![]() 为
为![]() 的中点.……………………………………4 分
的中点.……………………………………4 分
(Ⅱ)证法一:连接![]() 交
交![]() 于
于![]() ,因为
,因为![]() ,
,![]() ,
,![]() ,
,
由相似三角形易得![]() ,
,
∴![]() 不是
不是![]() 的中点,
的中点,
又∵![]() 为
为![]() 中点
中点
∴在平面![]() 中,直线
中,直线![]() 与
与![]() 相交 …………………………6分
相交 …………………………6分
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴直线![]() 与平面
与平面![]() 不平行. ………………………………………8分
不平行. ………………………………………8分
证法二:反证法,证明略.
(Ⅲ)过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,
,
则![]() 是二面角
是二面角![]() 的平面角 ……………………………10分
的平面角 ……………………………10分
注意到![]() ,
,![]() ,又
,又![]()
在![]() 中,
中,![]()
所以二面角![]() 的正切值为
的正切值为![]() ……………………………………………………12分
……………………………………………………12分
或应用空间向量知识解决:
(Ⅱ)以![]() 为原点,直线
为原点,直线![]() 、
、![]() 、
、![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,
轴,
建立空间直角坐标系(如图),
则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
则![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,这时取
,这时取![]() ……………………………6分
……………………………6分
∵![]()
而![]() ∴
∴![]() 与
与![]() 不垂直
不垂直
∴直线![]() 与平面
与平面![]() 不平行.……………………………8分
不平行.……………………………8分
(Ⅲ)由(Ⅱ)知平面![]() 的法向量为
的法向量为![]()
又平面![]() 的法向量
的法向量![]()
则![]() …………………………………………………………10分
…………………………………………………………10分
所以二面角![]() 的正切值为
的正切值为![]() .……………………………12分
.……………………………12分
20. 解:(1)由
![]() 恒成立,得:
恒成立,得:![]() 在
在![]() 时恒成立
时恒成立
当![]() 时
时![]() ……………………………2分
……………………………2分
当![]() 时即
时即![]() ,令
,令![]() ,
,![]()
![]() ……………………4分
……………………4分
![]() 时
时![]() ,
,![]() 在
在![]() 时为增函数,
时为增函数, ![]() 在
在![]() 时为减函数
时为减函数
∴ ![]() ∴
∴ ![]() …………………………………………………6分
…………………………………………………6分
(2)解:f(x)=x2-x+alnx,f′(x)=2x-1+![]() =
=![]() ,
,![]() .
.
(Ⅰ)当△=1-8a≤0,a≥![]() 时,f′(x)≥0恒成立,
时,f′(x)≥0恒成立,
f(x)在![]() +∞)上为增函数.……………………………………8分
+∞)上为增函数.……………………………………8分
(Ⅱ)当a<![]() 时
时
①当0<a<![]() 时,
时, ![]()
![]() ,
,
f(x)在![]() +∞)上为增函数.……………………………9分
+∞)上为增函数.……………………………9分
②当a=0时,f(x)在 [1,+∞)上为增函数.……………………………10分
③当a<0时,![]()
![]() ,故f(x)在
,故f(x)在![]() ,
,![]() ]上为减函数, f(x)在[
]上为减函数, f(x)在[![]() ,+∞)上为增函数.……………………………-11分
,+∞)上为增函数.……………………………-11分
综上:当![]() 时, f(x)的增区间为[1,+∞),无减区间;
时, f(x)的增区间为[1,+∞),无减区间;
当a<0时, f(x)的增区间是[![]() ,+∞),
,+∞),
减区间是![]() ,
,![]() ]. ……………………………12分
]. ……………………………12分
21. 解:(1)由题意可知椭圆![]() 为焦点在
为焦点在![]() 轴上的椭圆,可设
轴上的椭圆,可设![]() ,……2分
,……2分
由条件知![]() 且
且![]() ,又有
,又有![]() ,解得
,解得 ![]() , ………4分
, ………4分
故椭圆![]() 的离心率为
的离心率为![]() ,其标准方程为:
,其标准方程为: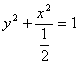 ………………6分
………………6分
(2)设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=, x1x2= ………………………………………………7分
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0 ………………………………………9分
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-)∪(,1) ………………………12分
22. 解:(1) 由 P1(t12,t1)(t > 0),… 1分,得 kOP1 = = tan = Þ t1 =
∴ P1(,) ……………………………2分
a1 = Q1Q0 = OP1 = ……………………………4分
(2) 设 Pn(tn2,tn),得直线 PnQn-1的方程为:y-tn = (x-tn2)
可得 Qn-1(tn2-,0)
直线 PnQn的方程为:y-tn = -(x-tn2),可得 Qn(tn2 + ,0)
所以也有 Qn-1(tn-12 + ,0),得 ![]() = tn-12 + ,……………………………6分
= tn-12 + ,……………………………6分
由 tn > 0,得 tn-tn-1 =
∴ tn = t1 + (n-1) = n ……………………………8分
∴ Qn(n(n + 1),0),Qn-1(n(n-1),0)
∴ an = QnQn-1 = n ……………………………10分
(3) 由已知对任意实数时 l∈[0,1] 时 n 2-2n + 2≥(1-l) (2n-1) 恒成立
Û 对任意实数 l∈[0,1] 时,(2n-1)l + n 2-4n + 3≥0 恒成立……………………………11分
则令 f (l) = (2n-1)l + n 2-4n + 3,则 f (l) 是关于 l 的一次函数.
Û 对任意实数 l∈[0,1] 时
Û ……………………………13分
Û n≥3或n≤1
又 ∵ n∈N *
∴![]() 或
或![]() 且n∈N * ……………………………14分
且n∈N * ……………………………14分
