江西省高中数学青年教师业务能力竞赛(解题)试题
[命 题:张园和]
本试卷分第I卷(选择题)和第II(非选择题)两部分,共150分.考试时间120分钟.考试结束,将本试卷和答题纸一并交回.
第I卷 (选择题 共60分)
注意事项:
1.答第I卷前,参赛选手务必在试卷及答题纸上将自己的单位、姓名、准考证号填在指定的位置.
2.所有试题的答案均应填入答题纸上的相应位置, 不能答在试卷上。未填入答题纸的部分一律按零分计.
一、本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.设集合![]() ,则实数a的取值范围是
,则实数a的取值范围是
A.![]() B.
B.![]() C.(-1,+∞) D.(-∞,-1)
C.(-1,+∞) D.(-∞,-1)
2.若![]() 都是实数,i是虚数单位,则
都是实数,i是虚数单位,则![]() =
=
A.1+2i B.1-2 i C.2+ i D.2-i
3.已知![]() 的值应是
的值应是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若函数![]() 的反函数为
的反函数为![]() ,则满足
,则满足![]() 的x的集合是
的x的集合是
A.(0,+∞) B.(1,+∞) C.(-1,1) D.(0, 1)
5.已知变量![]() 满足约束条件
满足约束条件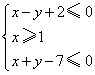 ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设随机变量![]() 服从标准正态分布
服从标准正态分布![]() ,已知
,已知![]() ,则
,则![]() =
=
A.0.025 B.0.050 C.0.950 D.0.975
7.已知两个等差数列![]() 和
和![]() 的前
的前![]() 项和分别为A
项和分别为A![]() 和
和![]() ,且
,且![]()
![]() ,则使得
,则使得![]() 为整数的正整数n的个数是
为整数的正整数n的个数是
A.2 B.3 C.4 D.5
8.已知椭圆![]() 有相同的准线,则动点P (n, m)的轨迹为
有相同的准线,则动点P (n, m)的轨迹为
A.椭圆的一部分 B.双曲线的一部分
C.抛物线的一部分 D.直线的一部分
9.半径为1的球面上的四点![]() 是正四面体的顶点,则
是正四面体的顶点,则![]() 与
与![]() 两点间的球面距离为
两点间的球面距离为
A. ![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
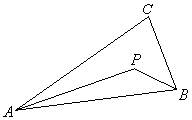 10.如图,设P为△ABC内一点,且
10.如图,设P为△ABC内一点,且![]()
则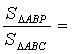
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.将号码分别为1、2、…、9的九个小球放入一个袋中, 这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b.则使不等式a−2b+10>0成立的事件发生的概率等于
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
12.已知定义域为R上的函数![]() 单调递增,如果
单调递增,如果![]() 的值
的值
A.可能为0 B.恒大于0 C.恒小于0 D.可正可负
第II卷 (共90分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题纸中的相应位置上.
13.在![]() 的展开式中,x5的系数为
.
的展开式中,x5的系数为
.
14.当![]() 时,不等式
时,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是 .
的取值范围是 .
15.若函数![]() = .
= .
16.对于函数![]() , 存在一个正数
, 存在一个正数![]() ,使得
,使得![]() 的定义域和值域相同, 则非零实数
的定义域和值域相同, 则非零实数![]() 的值为__________.
的值为__________.
三、解答题:本大题共6小题,共74分. 解答应写出必要的文字说明, 演算步骤或证明过程.
|
(1) 求![]() 的值;
的值;
(2)若对任意的![]() , 不等式
, 不等式![]() 恒成立, 求k的取值范围.
恒成立, 求k的取值范围.
18.(本题满分12分) 在九江市教研室组织的一次优秀青年教师联谊活动中,有一个有奖竞猜的环节.主持人准备了A、B两个相互独立的问题,并且宣布:幸运观众答对问题A可获奖金1000元,答对问题B可获奖金2000元,先答哪个题由观众自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题.若你被选为幸运观众,且假设你答对问题A、B的概率分别为![]() 、
、![]() .
.
(1) 记先回答问题A的奖金为随机变量![]() , 则
, 则![]() 的取值分别是多少?
的取值分别是多少?
(2) 你觉得应先回答哪个问题才能使你获得更多的奖金?请说明理由.

 19.(本小题满分12分) 已知函数
19.(本小题满分12分) 已知函数![]() (
(![]() R,且
R,且![]() )的部分图象如图所示.
)的部分图象如图所示.
(1) 求![]() 的值;
的值;
(2) 若方程![]()
在![]() 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.
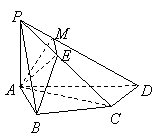
20.(本小题满分12分) 如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 是
是![]() 的中点.
的中点.
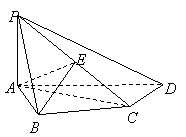 (1)证明
(1)证明![]() ;
;
(2)证明![]() 平面
平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
21.(本小题满分12分) 设不等式组  表示的平面区域为
表示的平面区域为![]() ,区域
,区域![]() 内的动点
内的动点![]() 到直线
到直线![]() 和直线
和直线![]() 的距离之积为2, 记点
的距离之积为2, 记点![]() 的轨迹为曲线
的轨迹为曲线![]() . 是否存在过点
. 是否存在过点![]() 的直线l, 使之与曲线
的直线l, 使之与曲线![]() 交于相异两点
交于相异两点![]() 、
、![]() ,且以线段
,且以线段![]() 为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
为直径的圆与y轴相切?若存在,求出直线l的斜率;若不存在, 说明理由.
22.(本小题满分14分) 已知函数![]() 及正整数数列
及正整数数列![]() . 若
. 若![]() ,且当
,且当![]() 时,有
时,有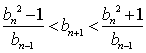 ; 又
; 又![]() ,
,![]() ,且
,且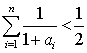 对任意
对任意![]() 恒成立. 数列
恒成立. 数列![]() 满足:
满足:![]() .
.
(1) 求数列![]() 及
及![]() 的通项公式;
的通项公式;
(2) 求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3) 证明存在![]() ,使得
,使得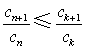 对任意
对任意![]() 均成立.
均成立.
参考答案
命 题:张园和
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | B | A | A | C | D | A | C | A | D | C |
| 题号 | 13 | 14 | 15 | 16 | 备 注 | |||||||
| 答案 |
|
| 1 |
| ||||||||
[1] 解: 画出数轴,由图可知![]() ,选B.
,选B.
[2] 解: 由![]() 得
得![]() ,所以
,所以![]() .
.
[3] 解: 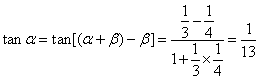 ,故选B.
,故选B.
[4] 解: 因为![]() , 所以
, 所以![]() ,于是原不等式为
,于是原不等式为![]() ,解得
,解得![]() .
.
[5] 解: 画出可行域(图略),为一个三角形区域,顶点分别为![]() .
.![]() 表示可行域内的点
表示可行域内的点![]() 与原点
与原点![]() 连线的斜率,当
连线的斜率,当![]() 时取最大值6,当
时取最大值6,当![]() 时取最小值
时取最小值![]() .故选A.
.故选A.
[6] 解: ![]() 服从标准正态分布
服从标准正态分布![]() ,
,![]()
![]()
[7] 解: 由等差数列的前![]() 项和及等差中项,可得
项和及等差中项,可得

![]()
![]() ,
,
故![]() 时,
时,![]() 为整数。故选D
为整数。故选D
[8] 解:由已知得: ![]() , 化简为
, 化简为![]() ,轨迹为椭圆的一部分. 故选A.
,轨迹为椭圆的一部分. 故选A.
[9] 解:半径为1的球面上的四点![]() 是正四面体的顶点,设AB=a,P为△BCD的中心,O为球心,则OB=1,OP=
是正四面体的顶点,设AB=a,P为△BCD的中心,O为球心,则OB=1,OP=![]() ,BP=
,BP=![]() a,由
a,由![]() 解得
解得![]() ,∴ 由余弦定理得∠AOB=arcos(-
,∴ 由余弦定理得∠AOB=arcos(-![]() ),∴
),∴ ![]() 与
与![]() 两点间的球面距离为
两点间的球面距离为![]() ,选C。
,选C。
[10]
解: 设![]() . 则
. 则![]()
![]() . 所以
. 所以![]() ,解得
,解得![]() .于是
.于是![]() .
.
[11] 解:甲、乙二人每人摸出一个小球都有9种不同的结果,故基本事件总数为92=81个. 由不等式a−2b+10>0得2b<a+10,于是,当b=1、2、3、4、5时,每种情形a可取1、2、…、9中每一个值,使不等式成立,则共有9×5=45种;当b=6时,a可取3、4、…、9中每一个值,有7种;当b=7时,a可取5、6、7、8、9中每一个值,有5种;当b=8时,a可取7、8、9中每一个值,有3种;当b=9时,a只能取9,有1种. 于是,所求事件的概率为![]() .
.
[12] 解: 由题设知,![]() 的图象关于点
的图象关于点![]() 对称. 又由已知,
对称. 又由已知,![]() 且
且![]() , 由
, 由![]() 在
在![]() 时单调递增知,
时单调递增知,![]() .故选C.
.故选C.
[13]
解: ![]() .
.
[14]
解: 由题设得![]() ,故只需求
,故只需求![]() .由单调性知,在
.由单调性知,在![]() 时,
时, ![]() ,所以
,所以![]() .
.
[15]
解: 易知![]() 为奇函数, 所以
为奇函数, 所以![]()
![]() .
.
[16]
解: 若![]() ,对于正数
,对于正数![]() ,
,![]() 的定义域为
的定义域为![]() ,但
,但![]() 的值域
的值域![]() ,故
,故![]() ,不合要求.若
,不合要求.若![]() ,对于正数
,对于正数![]() ,
,![]() 的定义域为
的定义域为![]() .由于此时
.由于此时![]() ,故函数的值域
,故函数的值域![]() .由题意,有
.由题意,有![]() ,由于
,由于![]() ,所以
,所以![]() .
.
17、解:(1)因为![]() 是奇函数, 所以
是奇函数, 所以![]() =0, 即
=0, 即![]()
又由![]() 知
知
(2) 解法一:由(1)知![]() , 易知
, 易知![]() 在
在![]() 上为减函
上为减函
数。又因![]() 是奇函数,从而不等式:
是奇函数,从而不等式:![]() 等价于
等价于
![]() .因
.因![]() 为减函数,由上式推得:
为减函数,由上式推得:![]() .
.
即对一切![]() 有:
有:![]() , 从而判别式
, 从而判别式![]()
解法二:由(1)知![]() .又由题设条件得:
.又由题设条件得:
![]()
即: ![]()
整理得: ![]()
![]() .上式对一切
.上式对一切![]() 均成立, 从而判别式
均成立, 从而判别式![]()
18、解:(1) 题意,![]() 的取值可以为0元,1000元,3000元
的取值可以为0元,1000元,3000元
(2) 设先答A的奖金为![]() 元,先答B的奖金为
元,先答B的奖金为![]() 元,则有
元,则有
![]() ,
,![]() ,
,![]() ,所以
,所以
![]() .
.
同理,![]() ,
, ![]() ,
,![]() .所以
.所以
![]() .
.
故先答A,能使所获奖金期望较大.
19、解:(1) 由图象易知函数![]() 的周期为
的周期为![]() (
(![]()
![]()
![]() )=
)=![]() ,∴
,∴![]() .
.
又, ![]() 且
且![]() , 即
, 即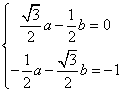 , 解得:
, 解得: ![]() . 所以,
. 所以,
![]()
![]() . [也可以按以下解释: 上述函数的图象可由
. [也可以按以下解释: 上述函数的图象可由![]() 的图象沿
的图象沿![]() 轴负方向平移
轴负方向平移![]() 个单位而得到,∴其解析式为
个单位而得到,∴其解析式为![]() .∴
.∴![]() ]
]
(2)![]() ∴
∴![]() ,∴
,∴![]() .设
.设![]() ,
,
问题等价于方程![]() 在(0,1)仅有一根或有两个相等的根.
在(0,1)仅有一根或有两个相等的根.
方法一:∵- m = 3t2 - t,t Î(0, 1). 作出曲线C:y = 3t2 - t,t Î(0, 1)与直线l:y = - m的图象.
∵t =![]() 时,y =
时,y =![]() ;t = 0时,y = 0;t = 1时,y = 2.
;t = 0时,y = 0;t = 1时,y = 2.
∴当 - m =![]() 或0≤-m<2时,直线l与曲线C有且只有一个公共点.
或0≤-m<2时,直线l与曲线C有且只有一个公共点.
∴m的取值范围是:![]() 或
或![]()
方法二:当 ![]() 仅有一根在(0, 1)时,令
仅有一根在(0, 1)时,令![]() 则
则![]() 得到
得到![]() ; 或
; 或![]() 时
时![]() ,或
,或![]() 时
时![]() (舍去)
(舍去)
当两个等根同在(0,1)内时得到![]() ,
,![]()
综上所述,m的取值范围是:![]() 或
或![]()
20、解:(1)证明:在四棱锥![]() 中,因
中,因![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,故
,故![]() .
.![]() ,
,![]() 平面
平面![]() .而
.而![]() 平面
平面![]() ,
,![]() .
.
 (2) 证明:由
(2) 证明:由![]() ,
,![]() , 可得
, 可得![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() .由(1)知,
.由(1)知,![]() ,且
,且
![]() ,所以
,所以![]() 平面
平面![]() .而
.而![]() 平面
平面![]() ,
,
![]() .
.![]() 底面
底面![]() 在底面
在底面![]() 内的
内的
射影是![]() ,
,![]() ,
,![]() .又
.又![]() ,
,
综上得![]() 平面
平面![]() .
.
(3) 解法一:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .则由(2)知,
.则由(2)知,![]() 平面
平面![]() ,
,![]() 在平面
在平面![]() 内的射影是
内的射影是![]() ,则
,则![]() .因此
.因此![]() 是二面角
是二面角![]() 的平面角.由已知,得
的平面角.由已知,得![]() .设
.设![]() ,可得
,可得
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,则
,则
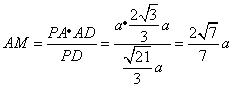 .
.
在![]() 中,
中,![]() .所以二面角
.所以二面角![]() 的大小是
的大小是![]() .
.
解法二:由题设![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,则平面
,则平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,故
,故![]() 平面
平面![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,故
,故![]() .因此
.因此![]() 是二面角
是二面角![]() 的平面角.
的平面角.
由已知,可得![]() ,设
,设![]() ,
,
可得![]() .
.

![]() ,
,![]() .
.
于是,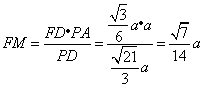 .
.
在![]() 中,
中,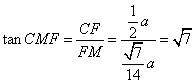 .
.
所以二面角![]() 的大小是
的大小是![]() .
.
 21、解:由题意可知,平面区域
21、解:由题意可知,平面区域![]() 如图阴影所示.设动点为
如图阴影所示.设动点为![]() ,则
,则
![]() ,即
,即
![]() .
.
由![]() 知
知![]() ,x-y<0,即x2-y2<0.
,x-y<0,即x2-y2<0.
所以y2-x2=4(y>0),即曲线![]() 的方程为
的方程为
-=1(y>0)
设![]() ,
,![]() ,则以线段
,则以线段![]() 为直径的圆的圆心为
为直径的圆的圆心为![]() .
.
因为以线段![]() 为直径的圆
为直径的圆![]() 与
与![]() 轴相切,所以半径
轴相切,所以半径 ![]() ,即
,即
![]()
因为直线AB过点F(2,0),当AB ^ x轴时,不合题意.所以设直线AB的方程为y=k(x-2).代入双曲线方程-=1(y>0)得:
k2(x-2)2-x2=4,即
(k2-1)x2-4k2x+(8k2-4)=0.
因为直线与双曲线交于A,B两点,所以k≠±1.于是
x1+x2=,x1x2=.
故 AB==
==x1+x2=,
化简得:k4+2k2-1=0
解得: k2=-1 (k2=--1不合题意,舍去).
由△=(4k2)2-4(k2-1)(8k2-4)=3k2-1>0,又由于y>0,所以-1<k<- .
所以, k=-
22、解:(1) 由![]() 得:
得:![]() .因为
.因为![]() 是正整数列,所以
是正整数列,所以![]() .于是
.于是![]() 是等比数列. 又,
是等比数列. 又,![]() , 所以
, 所以![]() .
.
因为![]() ,所以
,所以![]() ,于是:
,于是:![]() ,说明
,说明![]() 是以2为公比的等比数列. 所以
是以2为公比的等比数列. 所以
![]()
因为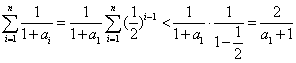 , 由题设知:
, 由题设知: ![]() ,解得:
,解得:![]() 。
。
又因为![]() 且
且![]() ,所以
,所以![]() 。
。
于是![]() 。
。
(2) 由![]() 得:
得:![]() .由
.由![]() 及
及![]() 得:
得:![]()
设![]() ①
①
![]() ②
②
当![]() 时,①式减去②式, 得
时,①式减去②式, 得
![]()
于是, ![]()
这时数列![]() 的前
的前![]() 项和
项和![]() .
.
当![]() 时,
时,![]() .这时数列
.这时数列![]() 的前
的前![]() 项和
项和![]() .
.
(3) 证明:通过分析,推测数列![]() 的第一项
的第一项![]() 最大,下面证明:
最大,下面证明:
![]() ③
③
由![]() 知
知![]() ,要使③式成立,只要
,要使③式成立,只要![]() ,
,
因为![]()
![]()
![]() .
.
所以③式成立.
因此,存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.